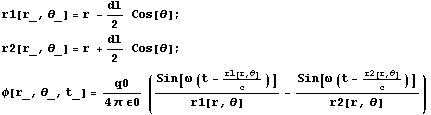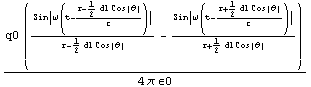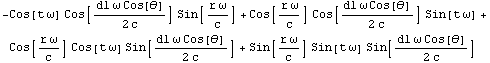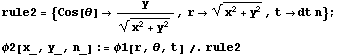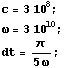いままで電気双極子を中心にやってきましたが、今回も電気双極子に 絡んだ問題を取り上げます。今回は時間的に振動する電気双極子 ｑ₀ sin(ωt) dl です。

時刻t=0での電気双極子の中心を原点に選び、極座標で考えます。 点 P=(r,θ,0)に生じる電磁ポテンシャルを視覚化しましょう。

古典電磁気学の知識より、 スカラーポテンシャルは

となります。r1 および r2 は近似(余弦定理を使って、 dl²を無視する） をします。

電場は、このまま視覚化しようとしてもプロットする関数のなかにあまりに 0 に近い数が含まれていると、Mathematica はうまくプロットしてくれず、 エラーになります。r1, r2 にしたのと同程度の近似を他の部分にも適用して やります。

が充分 0 に近いので、次の変換ルール

を適用しましょう。それにはまず三角関数を展開してやらなければなりません。 試しに第1項を展開してみましょう。展開する関数は Expand でした。

おかしいですね。ぜんぜん展開してくれていません。実は Mathematica はデフォルトでは三角関数の展開を抑制します。 これを行いたいときにはオプションが必要です。以下を試してみましょう。

のように展開してくれます。同じ要領でスカラーポテンシャルを sine 関数の中身を 展開した形で定義し直して Expand し、 rule1 を適用しましょう。

出力は複雑なので省略します。なんだかよくわからないので、簡単にしましょう。

（出力の具体的な形はバージョンにより異なることがあります。その場合、 近似の範囲で同等の結果になっていることを確かめましょう。） まだ dl の2乗のオーダーが分母に残っているので、もう少し近似をしましょう。

さらに、前回同様、 でスケールしてやります。（1とおくことに相当します。）ついでに Simplify しましょう。(うまくいかない場合は % に直接式を入れて下さい。)

このままだと視覚化しにくいので、前回と同じようにカーテシアン座標系に変換します。 ついでに時間 t を、とびとびの変数に変換します。

x, y, n に具体的な値を入れて、関数が正しく定義されているかどうか確かめてみましょう。 どうも x, y, n を変数として扱ってくれていないようです。出力された式をコピーして、 もう一度関数を定義してみましょう。今度はうまくいくはずです。

あとは視覚化です。 次のような数値を代入してみましょう。

dt は1周期 ぶんを10 個に分割して描かせるための定数です。 dt の間隔で時間 t を増やしていき、その時間変化をアニメーションで視覚化します。

そのためには Animate というコマンドを使います。 Animate[Plot3D[...], {n, a, b, dn}] で n を a から b までステップ dn で変化させたグラフを描いてくれます。 今の場合、1周期ぶん描かせれば充分です から、n は 0 から 9 まで動かせばよいですね。

電磁波が伝わる様子が実感できたでしょうか？