時間変化する電磁ポテンシャルの解

Maxwellの方程式にLorentz条件を課すと、ポテンシャルφに対して以下の波動方程式が得られる：

　

これを解く為に、ポテンシャルおよび電荷密度をフーリエ変換する。

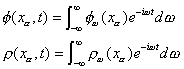
その逆変換は、

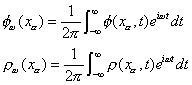
これをもとの式（1）に代入すると、

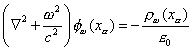
が得られる。この式をとく為にグリーン関数の方法を用いる｡グリーン関数Ｇは、

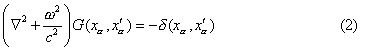
で定義される関数であるが、これを求めると、元のポテンシャルは、

によって得ることが出来る。 [ 訂正：(1/2 Pi) は 1/epsilon_0 ]したがって問題はＧを求めることに帰着した。

まず、以外のすべての点では、

ここで、である。[ 訂正：k -> k^2 ]

この解は簡単に積分でき、

となる。この定数Ａは、周りの微小球殻内の体積積分を、（2）に対して行うことによって決定することができる。まず左辺は、

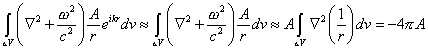
右辺は

したがってとなる。したがってＧの表式は、

となる。このＧを使ってもとのフーリエ変換されたポテンシャルを求めると、

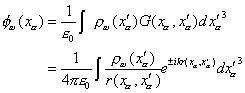
これからもとのポテンシャルは、

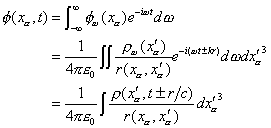
この式は、におけるポテンシャルは、における電荷によって決まるという

ことを意味している｡因果律から考えて、の解は、未来の電荷によって過去の電場

が決まることになるので、棄却すれば、結局、

となる。

時間変動する電気双極子まわりのポテンシャル

（3）式を用いて時間変動する電気双極子のまわりのポテンシャルを調べる。

まず電荷密度分布は、

[ 訂正：デルタ関数の中の d の前の符号の + - がそれぞれ逆 ] これを（3）式に代入すると、

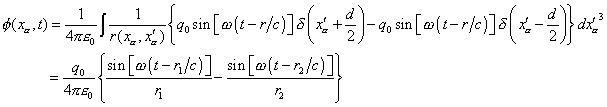
ここで、である。