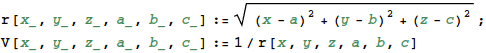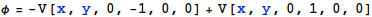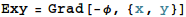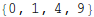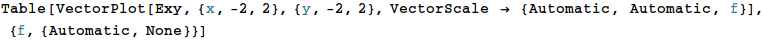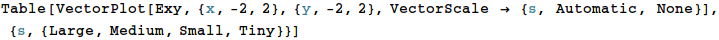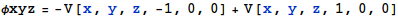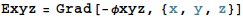電場の視覚化

１．電気双極子がつくる電場

今回はまず、前回取り上げた電気双極子を例に電場の視覚化を行います。後半は電気双極子が絡む静電場の問題を実際に解いてみます。今回の提出課題ではその類似問題を各自にやってもらいます。

a)ベクトル場を視覚化する（2次元）

前回と同じユーザー定義関数を使います。

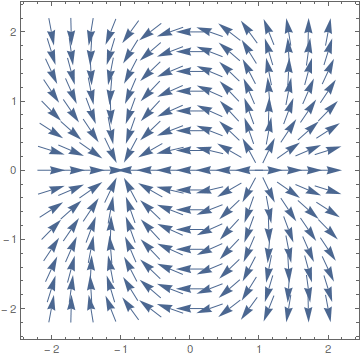
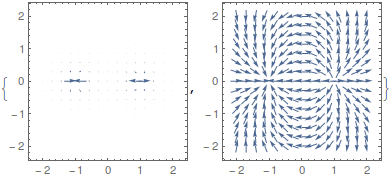
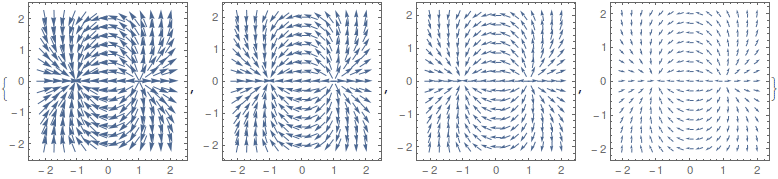
電気双極子として、座標(-1, 0, 0)に電荷-1、座標(1, 0, 0) に電荷+1を置いたものを仮定し、そのときの電場（定義域をｘｙ平面に限定したもの）を視覚化します。そのためにまずｘｙ平面に限定したポテンシャルφを定義します。

ｘｙ平面に限定した電場EをE=-gradφで定義します。

ベクトル解析の関数は Grad の他にも Div, Curl など使えます。ヘルプで Vector Analysis などを見て、調べてみてください。

続いて VectorPlot を用いてベクトル場を可視化します。

ベクトルの描画を VectorScale のオプションを使って調節しています。 VectorScale の性質を見る前に準備で、表を作成する Table を説明します。次の例でその機能は理解できると思います。

VectorScale の3つの引数のうち3番目は、矢印の長さを決める方法を指定します。 Automatic とするとそのベクトルの大きさに比例した長さの矢印を描画します。 None とするとすべての矢印の長さが一定になります。

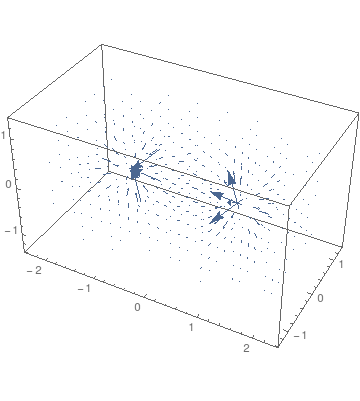
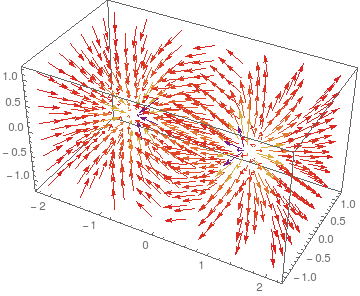
VectorScale の1番目の引数は、矢印の長さの倍率を指定します。 Large, Medium, Small, Tiny などを使って指定できます。

また数値を使っても指定できます。更に詳しいことは、ヘルプで VectorPlot を見てください。

b)ベクトル場を視覚化する（3次元）

ベクトル場を3次元でプロットするには VectorPlot3D を使います。まず、電気双極子の3次元のポテンシャルと電場を定義します。

続いて VectorPlot3D で描画します。

様々なオプションを使うことで、様々な描画が可能です。各自ヘルプの VectorPlot3D を見るなどして、個性的な描画をしてみてください。