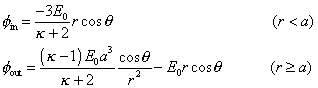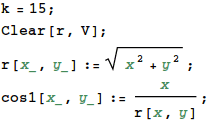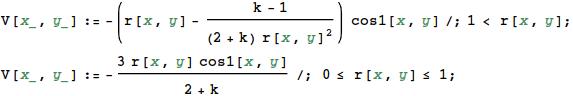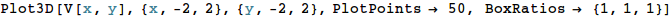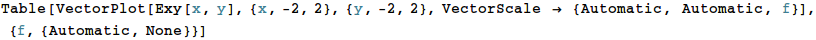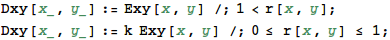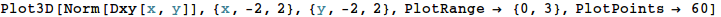|
2.総合問題 真空中の一様電場 E0 の中に半径 a、比誘電率 κ の誘電体球を置いたときの各部の電位、 電場、電束密度を求めなさい。 |
| a) 電位の視覚化 |
|
球内部には一様な誘電分極 P が誘起されます。 また球外部の任意の点では、球の中心に双極子モーメント P=qd ができているとみなして計算をすすめることができます。 双極子モーメントを形成する2つの点電荷 +q, -q は、 実際にはその点を中心とする半径 a の球内に電荷密度 +ρ(-ρ)で 一様分布しており、2球の共通部分では電荷は互いに打ち消しあって 0 となり、両端の厚さ d の領域に電荷が現れるので、 実際の状況と同じであることがわかります。 ここで誘起される双極子モーメントは、
球内外の電位φin,φoutは、 電場と垂直な yz 平面中に原点に選べば
この解の厳密な導出はこちら
pdf
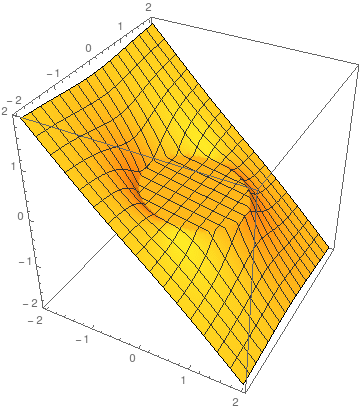
にありますので、 わからない人は必 さてMathematicaでこの解を視覚化してみましょう。 ためしにκ=15でaとE0 は1にして描いてみます。 カーテシアン座標に変換してやれば、通常の3次元プロットが可能です (RevolutionPlot3D を使えば円柱座標のままでもプロット できます。時間のある人はやってみましょう)。
ここで /; は Condition の意味で、条件が満たされたときだけ適用される という定義になっています。
ここで PlotPoints は解像度(描画に1軸方向に何点使うか)を指定しています。 多いほど滑らかになりますが時間がかかります。各自調節してください。 |
| b)電場の視覚化 |
|
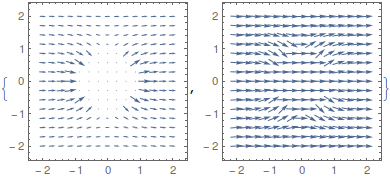
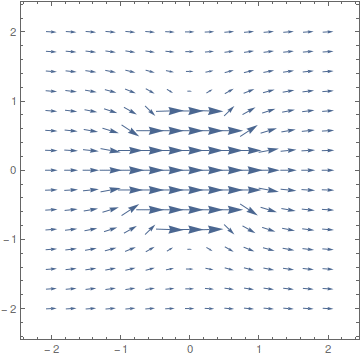
電場は、前半でやったように、電位の gradient を計算することより求まります。ここでは Exy を x,y の関数のように定義しました。
|
| c)電束密度の視覚化 |
|
電束密度も同様に視覚化できます。
電束密度の大きさは、以下のようになります。
|