������g�b�v�ɖ߂�
4/20�@�@5/11�@�@5/18�@�@6/1�@�@6/22�@�@7/13�@�@7/26�@�@8/24�@�@9/14�@�@9/28�@�@10/13�@�@11/30�@
�@12/21�@�@1/11�@�@1/25�@�@2/8�@�@2/29�@�@3/14�@�@4/7�@�@4/18�@�@5/9�@�@5/23�@�@6/6�@�@6/20�@�@7/25�@�@8/21
Glass, G. V., & Hopkins, K. D., (1996). Statistical methods in education and
�@�@ psychology. Boston, MA: Allyn & Bacon.
2007/04/20�@(Ch. 1-3, pp. 1-48)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
1. Introduction (p. 1)
1.1 The "Image" of Statistics (p. 1-2)
���@���v�I�ȊT�O����@���������邱�ƂŁA�����ɂ��Ă����M�����ސ��������炵�A�ʓI�ȏ��������g����悤�ɂȂ�B���v���@�̔��B��2�̑S���قȂ�e�����y�ڂ��B1�͋L�q���v�Ɋւ�邱�Ƃł���A����1�͊m���I�Ȑ������v�Ɋւ�邱�Ƃł���B2�͂���8�͂܂ł��L�q���v�A������9�͈ȍ~�Ő������v�ɂ��ĐG���B
1.2 Descriptive Statistics (p. 2)
���@�L�q���v�ɂ́A�\�ɂ��ĕ\�����ƁA�`�ʂ��邱�ƁA�f�[�^�̋L�q���܂ށB�����͐g����e�X�g���_�Ȃǂ̗ʓI�Ȃ��̂��A�������w�̐�U�ȂǃJ�e�S���J���f�[�^�̂悤�Ȏ��I�Ȃ��̂��������Ƃ��ł���B
1.3 Inferential Statistics (p. 2-3)
���@�����ȃT���v���f�[�^����S�̂𐄑����邱�Ƃ��܂ށB�܂�A�T���v�������W�c�̏������ނ��Ƃ��������v�̖ړI�ł���B�T���v���̋L�q�I�������A�덷��m�邱�Ƃ␄�����v�̋Z�p�ɂ���ĕ�W�c�S�̂Ɉ�ʉ����邱�Ƃ��ł���B
���@�������v�ɂ����ẮA�����̃f�U�C���ƕ��͂��d�v�ł���B�����ɂ���āA�ϐ��Ԃ̈��ʊW��]�����邩��ł���B
1.4 Statistics and Mathematics (p. 3-4)
���@���v�̌����͉��p���w�̈ꕔ�ł��邪�A�ʏ�l�����Ă���قǂ́A���w�̒m����K�v�Ƃ��Ȃ��B
���@���̖{���g���ɂ������āA��x�����ł͂Ȃ����x���ǂ݁A���e�͂����S�Ɋw��ł����K�v�����邾�낤�i1�̏͂ɏ����Ă��邱�Ƃ��A���̏͂ł͑O��ɂȂ��Ă��邽�߁j�B�e�͂̍Ō��Mastery Test�����邽�߁A��������p����Ɨǂ��B�܂��A���Mastery Test�����邱�ƂŁA���̏͂ɂ�����S�̏������ł��邩������Ȃ��B
1.5 Case Method (p. 4-5)
���@���̖{�ł́ACHAPMAN (10�N�ԁA200���̑�l���������̕ϐ��ɂ��Ē��ׂ�ꂽ�R���X�e���[���ɂ��Ă̌���)�AHSB (600���̍��Z���ɂ��Ẵf�[�^)�AEXERCISE (40�l�ɑ���^���Ƌi���̃f�[�^)��3��ނ̃f�[�^��p���邱�Ƃɂ���āA���z�I�Ȏ��K���\�ł���B
1.6 Our Targets (p. 5)
���@���̖{�ł́A�ʓI�ɕ\���������ɂ��Ă̈�ʓI��literacy�A���v�́u����҂̒m���v�A���v�̃R�}���h�A��荂�x�Ȍ����ɏ\���ȓ��v���@�̒m���邱�Ƃ��ł���ł��낤�B
2. Variables, Measurement, Scales (p. 6)
2.1 Variables and Their Measurement (p. 6)
���@�L�q���v�E�������v�́u�ϐ��v��p����B�ϐ��Ƃ́A�ϑ��Ώۂɂ�����1�ȏ�̓����ł���i�l�̔N��Ȃǁj�B���v�́A�ϑ��Ώۂ�`�ʂ���̂ɗp������B
2.2 Measurement: The Observation of Variables (p. 6-7)
���@�ϐ������v�I�Ɉ�����O�ɁA�ϑ�����Ȃ���Ȃ�Ȃ��B�܂�A����ꂽ��A�ʂŕ\���ꂽ��A���ނ��ꂽ�肵�Ȃ���Ȃ�Ȃ��B����Ƃ́A���ŕ\�����ϑ��ł���B����Ƃ́A���[���Ɋ�Â��Đ������蓖�Ă邱�Ƃł���B����́A�ł��邾�����m�őÓ��łȂ���Ȃ�Ȃ��B
2.3 Measurement Scales: Nominal Measurement (p.7)
���@�`���I�ɁA4�̑���i�ϐ��j������A���ꂼ��������Œ�`���A���v�I�Ȏ����Ƌ��Ɉ������Ƃɂ���B
���@���`�ϐ��͍ł������I�Ȍ`���ł���B���镪�ނɑ�������̂��A���̓��肩��͓����ł���悤�ɕ����邱�Ƃł���B�Ⴆ�A0�������A1��j���Ƃ���悤�Ȃ��Ƃł���B�������`�ϐ��݂̂�p����̂ł���A���̐��̓��������p���邱�Ƃ��ł��Ȃ��B�܂�A1��2��4�Ƃ͈Ⴄ�A�Ƃ������Ƃł���B
���@����Ȍ�̕ϐ��ł́A�T�C�Y�ŏ��Ԃ��t�����邱�ƁA�����ł��邱�ƁA�揜�ł��邱�ƁA�Ƃ����������������Ă����B
2.4 Ordinal Measurement (p. 7-8)
���@�����ϐ��́A����ϐ��̒��x��ʂ���ʂł���Ƃ��ɂ̂ݗp������B�Ⴆ�A�����N�t��������Ƃ��ł���B�p�[�Z���^�C�����ʂ��A�����ϐ���1�ł���B
2.5 Interval Measurement (p. 8)
���@�Ԋu�ϐ��ł́A�ϑ��Ώۂ̍��𐔂ŕ\�����Ƃ��ł���B�Ⴆ�A90�x��100�x�̍���50�x��60�x�̍��Ɠ����ł���B�������A100�x��50�x�̔{�ł͂Ȃ��B�Ԋu�ړx�́A0�Ƃ͜��ӓI�Ȃ��̂ł���A���̓������S���������Ƃ������킯�ł͂Ȃ��B
���@�Ԋu�ϐ��͏����ϐ��ɕϊ��ł��邪�A���̋t�͒ʏ�͂ł��Ȃ��B
2.6 Ratio Measurement (p. 8-9)
���@�䗦�ϐ��ƊԊu�ϐ����قȂ�_�́A�[�������̓������������Ƃ��Ӗ�����_�ł���B�䗦�ϐ��͊Ԋu�ϐ��ł�����B�]���āAA��B��2�{�A�ȂǂƏq�ׂ邱�Ƃ��ł���B���̔䗦�ɈӖ������邽�߁A�䗦�ϐ��Ɩ��Â����Ă���B
2.7 Interrelationships Among Measurement Scales (p. 9-10)
���@�ϐ��̃��x������肷�邱�Ƃ͏�ɊȒP�ł���킯�ł͂Ȃ��B�Ⴆ�AIQ��130�̐l��IQ��100�̐l��30%�������ǂ��킯�ł͂Ȃ����AIQ��70��100�̐l�̍��ƁA100��130�̐l�̍��������ł͂Ȃ����낤���i�܂�A�Ԋu�ړx�ɂ͓��Ă͂܂�Ȃ��j�AIQ�͏����ړx�ł͂Ȃ��B�Ȃ��Ȃ�A���������ړx�ł���Ȃ�A�����݂̂�����邾�낤����ł���B
���@�܂��A�e�X�g��100%�̓_��������l��50%�������Ȃ������l�̔{�A�\�͂�����̂��낤���B100%������l�̂ق���50%�Ƃ����l�����\�͂�����A�Ƃ������Ƃ��������Ȃ��ł��낤�B
���@�ȑO�́A����ړx�̏d�v�����֒����ꂷ���Ă����B�������A�ړx�͂ǂ̂悤�Ɍ��ʂ����߂���悢���Ƃ������Ƃɂ��Ă̌��_�������炵�Ă͂���Ȃ��B
2.8 Continuous and Discrete Variables (p. 10-11)
���@�̏d��N��Ȃǂ̂������̕ϐ��͘A���ϐ��ł���A�����ɂ���q���̐��Ȃǂ͗��U�ϐ��ł���i�����_���g���Ȃ��j�B�A���ϐ��𐳊m�Ɏ������Ƃ͕s�\�ł���i�����_�̊W�Ȃǂ̂��߁j�B
2.9 Chapter Summary (p. 11)
���@�ϐ��Ƃ͊ϑ��Ώۂ��������ł���B����Ƃ͊ϑ��Ώۂɐ��Ă͂߂邱�Ƃł���B�����ɂ́A���`�ϐ��A�����ϐ��A�Ԋu�ϐ��A�䗦�ϐ����܂܂��B�����̎ړx�͑�����@�ɂ���Ă̂��܂���̂ł͂Ȃ��A�^����ꂽ���̉��߂ɂ���Ă����܂�B
2.10 Case Study (p. 11-12)
���@CHAPMAN�̃f�[�^�ŁA�N��A�S�����k�̌����A�S���g���̌����A�R���X�e���[�����x���A�g���A�̏d�A���������i0 = No, 1 = Yes�j�AID number��ϐ��Ƃ����B���ꂼ�ꂪ�ǂ̎ړx�ł��낤���B�N��A�g���A�̏d�A�����A�R���X�e���[�����x���͔䗦�ϐ��Acase number�͖��`�ϐ��ł���B���������́A���`�ϐ��������̓J�e�S���J���ȕϐ��ł���B
���@�ǂꂪ���U�ϐ��ł��낤���BID number�Ɠ��������݂̂����U�ϐ��ŁA���̑��͘A���ϐ��ł���B
3. Frequency Distributions and Visual Displays of Data (p. 15)
3.1 Tabulating Data (p. 15)
���@���������Ԃɕ��ׂ邱�Ƃ͏����ɂ͂Ȃ邪�A���z�̍ł��d�v�ȓ�����`�ʂ��邱�Ƃ͂ł��Ȃ��B���z�̓����́A�ϑ��Ώۂ��ɕ����邱�Ƃɂ���Ė��炩�ɂȂ�B���̕����鐔�͜��ӓI�ł͂��邪�A10�ȏオ�g���邱�Ƃ������B���̂悤�ɃO���[�v�����ĕ��ׂ邱�Ƃ��Agrouped frequency distribution�ƌĂԁB
3.2 Grouped Frequency Distributions (p. 16-18)
���@�p�x���z����ɂ́A����5�̎菇�ށB
(a) �͈͂�m��
�E�ł��傫�Ȋϑ����l�Ə������ϑ����l�̍����͈͂ł���B
(b) �O���[�v�̐������߂�
�E����͜��ӓI�ł���B�A���A�Ԋu��20��30�ɂȂ�Ȃ��悤�ȂƂ��ɂ́A�ϑ������O���[�v����10�{�ȏ�ɂȂ�悤�ɂ��������悢�B�A���A�O���[�v������������ƒl����E���A�O���[�v�������Ȃ�����ƕ��z���e���Ȃ肷����B
(c) �Ԋu�̐��������߂�
�E�͈͂𗝑z�̃O���[�v���Ŋ���ƁA��܂��ȊԊu�����߂邱�Ƃ��ł���B�S�Ă̐��l���A�ǂꂩ1�ɂ��Ă͂܂�悤�ɂ��Ȃ���Ȃ�Ȃ��i120-140, 140-160�A�Ƃ���̂ł͂Ȃ��A120-139, 140-159�Ƃ���A�Ȃǁj
(d) �ϑ������O���[�v�P�ʂɍ��킹��
�E���ꂼ��̊Ԋu�ɂ��āA�e�ϑ������v����悤�ȓ`���I�� "picket fence" �̕��@�ł��ǂ����A�ϑ����������ꍇ�ɂ�Tukey (1977) �̕��@���L���ł���B�ŏ���4�͎l�p�ɂȂ�悤�ɓ_�ŕ\���A����4�͂����̓_���ӂɂȂ�悤�ɂȂ��A����2��Ίp���ɂ���悤�ɂȂ����ƂŁA10��\�����Ƃ��ł���B
(e) ���ꂼ��̍��v�𐔂���
3.3 Grouping and Loss of Information (p. 19)
���@statistical summary�́A�S�Ă�`�ʂ��Ȃ��B�O���[�v�����邱�Ƃɂ���ď������B�O���t�ɂ��ẮA�g���₷���╪����₷���ƁA���̑����̃g���[�h�I�t���N����B
3.4 Graphing a Frequency Distribution: The Histogram (p. 19-20)
���@���z���O���t������Ƃ��ɍł��ǂ��g����3�̕��@�́A�q�X�g�O�����A�p�x���p�`�i�܂���O���t�j�A�x�����z�Ȑ��ł���B
���@�q�X�g�O�����͖_�ɂ���ĕ\����A�_�̒��������͈̔͂Ɋ܂܂��p�x��\�� (Figure 3.1)�B����́A�p�x�����ł͂Ȃ�������\������̂ɂ��p������B�ϑ����S�̂Ŋ���A�������Z�o�����B�����̃q�X�g�O�����̕������D�܂��B�Ȃ��Ȃ�A200�l��6���A�Ƃ�������3%�ƌ������ق����Ӗ������邩��ł���B
3.5 Frequency and Percentage Polygons (p. 20-22)
���@�p�x���p�`�̓q�X�g�O�����Ǝ��Ă��邪�A�ϑ��l�̎n�_�ƏI�_�̃[���̕�����t��������B�p�x���p�`�ł́A���ꂼ��̊Ԋu�̒��S���_�ŕ\����A���ꂼ�ꂪ����� (Figure 3.3)�B�q�X�g�O�����Ɠ��l�ɁA�������������l�ʼnE�����傫���l�ł���B�������`�ϐ���J�e�S���J���ȕϐ���p����̂ł���A���ꂼ��̐����A�����Ă��邱�Ƃ����肷��p�x���p�`��misleading�ł��邽�߁A�q�X�g�O�����̕����]�܂����B
3.6 Types of Distributions (p. 23-24)
���@���z�̌`��\�����ʗp�ꂪ����Bp. 23�̕��zA�͐��K���z�ł���A���E�Ώ̂̂肪�ˌ^�̋Ȑ��ł���B�����̕ϐ��͂قڐ��K���z����B���K���z�ɂ��Ă�6�͂ň����B
���@�J�[�uB�͍��E�Ώ̂ł��邪�A2�ɕ�����Ă��� (bimodal) �ł��邽�ߐ��K���z�ł͂Ȃ��B�Ⴆ�A�l�Ԃ̐g�����O���t�ɂ���ƁA�����̕��ϐg���ƒj���̕��ϐg���Ƃ����A2�_�ŎR���ł���ł��낤�B����2�̎R�̑傫�����قȂ��Ă����ꍇ�A�傫�����̎R��major mode�A���������̎R��minor mode�ƌĂԁB2�����Ȃ����̂̕��z�́A���ʂȌ`��bimodal���z�ł���B
���@�J�[�uC�͒����`�ł���A���E�Ώ̂ł���A�l���S�Ĉ��ł���B����1�̂������낪1������ꂽ��A1����6�܂ł��o��p�x�͂قڒ����`�̌`�ɂȂ邾�낤�B
���@�J�[�uD��E�́A��Ώ̂ȕ��z�ł���B����͘c�x�ɂ���ĕ\�����BD��positively skewed�ł���AE��negatively skewed�ł���B
���@�A���A�����̕��z���S�đ��ݔr���I�ł���킯�ł͂Ȃ��̂ŁA���ӂ��ׂ��ł���B
3.7 Cumulative Distributions and the Ogive Curve (p. 24-25)
���@�x�����z�Ȑ��́A�p�[�Z���^�C����\���̂ɗL���ł���B�ݐϓI�A�Ƃ����̂��x�����z�Ȑ��̌����ł��� (Figure 3.6)�B
3.8 Percentiles (p. 25-26)
���@�p�[�Z���^�C���Ƃ́A���̊ϑ��l�����p�[�Z���g�ڂɂ��邩�A�Ƃ������Ƃł���B�ł́A�R���X�e���[�����x���̒����l�͂������낤���H�����l�Ƃ́A�p�[�Z���^�C�����ʂ�50�ԖڂƂ������Ƃł���B
���@�����p�[�Z���^�C�����ʂ𐳊m�ɏo�������ꍇ�����邾�낤�B����40�l����Tom��37�l������ɂ���̂ł���ATom�̃p�[�Z���^�C�����ʂ� (37 + 0.5)/40�~100�ŕ\�����B0.5�Ƃ́ATom�̓��_�̔�����\���Ă���B
���@�p�[�Z���^�C���͌l�̃p�t�H�[�}���X�����߂���̂ɂ͂ƂĂ��L���ł��邪�A�������v�ŗp����Ƃ��ɂ͏d��Ȗ�肪����B�Ⴆ�A2�O���[�v�̕��ϓI�ȃp�t�H�[�}���X�ɗL�Ӎ������邩�ǂ����ׂ�Ƃ��ɂ́A�p�[�Z���^�C�����ʂł͂Ȃ��A���̂܂܂̓��_��W�������ꂽ���_��p����B
3.9 Box-and-Whisker Plots (p. 26-28)
���@����͗�����box plot�ƌĂ��B����box�̓p�[�Z���^�C�����ʂ�25����75�ʂ�\���Abox�̒��̐��͒����l��\���B2�{�̐��́A�O��l����������͊ϑ��l�̏���Ɖ����܂ł�\���B���̐��́Abox�̒�����1.5�{�����x�ł���A����ȏ㗣�ꂽ���̂͊O��l�Ƃ��ē_�ŕ\���B
���@box plot��2�ȏ�̕��z���r����Ƃ��ɗL���ł��� (Figure 3.8)�B����ɂ���āA�����̕��������������_�������A�����̂ق������_�̂��������A�����w�Z�̐��k�ł������̐��k�Ɠ������炢�������_�̊w��������A�����̕����Ⴂ���_�̐��k�������Ƃ�������A�Ƃ������Ƃ�������B
3.10 Stem-and-Leaf Displays (p. 28-30)
���@stem-and-leaf display�Ƃ������@������B���v�ł͂Ȃ��A�ϑ��l�̍Ō�̒l��p���� (Figure 3.10)�B�c�̐����u���v�ł���A�Ō�̐��l���u�t�v�ł���B
3.11 Time-Series Graphs (p. 31)
���@time-series graph��p����ƁA������ω����A���̕\�����@�ł͂ł��Ȃ����@�ŕ`�ʂ��邱�Ƃ��ł��� (Figure 3.11)�B
3.12 Misleading Graphs: How to Lie with Statistics (p. 31-37)
���@�O���t��\�́A�^����`����Ƃ������A��`�Ƃ��Ďg��ꂤ�邽�߁Amisleading�ɂȂ肤��B
(a) Distorted Representation
�E�s�N�g�O���t��p���āA�p�x��1�̊G�����ŗp���邱�ƂŁA�{���͒����݂̂��p�x��\���Ă���̂ɂ��ւ�炸�A���Ă���l�͖ʐς��p�x���Ǝv���Ă��܂��B
(b) Misleading Scaling and Calibration
�EFigure 3.12C�̂悤�ȏꍇ�ɂ́A�n�_�����ӓI�ł���B�䗦�ړx�̏ꍇ�ɂ́A�n�_��0�ł���ׂ��ł��邪�A�֒�����Ă��܂��Ă���B
(c) Combination Graphs
�E�����Ƃ������O�ꂽ���@�ł���B�ϐ���s�K�ȕ��@�ő��肵�Ă��邽�߂ɋN���� (Figure 14)�B
���@�܂��A�O���t�ɏ�����ꂷ����ƍ����̂��Ƃł��� (Figure 3.15)�B
3.13 Chapter Summary (p. 37)
���@�����̕ϐ��͐��K���z���邪�A���̕��z�̎d�����悭���邱�Ƃł���B�܂��A�p�x�͗l�X�ȕ��@�ŕ\�����B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�X�{�j
�f�B�X�J�b�V�������R�����g
2.7�ɂ�����
�������͓��ɏd�v
�A���P�[�g�̂悤�Ȏړx�f�[�^�ɂ��āASPSS�ɂ����ĕ��͂��邱�Ƃ͑Ó��Ȃ̂��ǂ����A�Ƃ������₪�o���B����ɂ��ẮALikert Scale��p���Ă���_����ǂ�ł݂悤�A�Ƃ�����Ă��Ȃ��ꂽ�B
�\�������ړx�ϐ��Ȃ̂Ńm���p�����g���b�N�@�ɂ�镪�͂����Ă���ꍇ�ƁA�����ړx�ł����Ă��A���̃f�[�^�����K���z���Ȃ��A�A���ϐ��Ƃ݂Ȃ��Ă��邩��ł��낤���A�p�����g���b�N�@���g�p���ĕ��͂��Ă����������B���̏ꍇ�A5�i�K���x�̃X�P�[���ł͐��K�������Ă��邩�͋^�킵�����A�ޏ���łȂ��Ƃ��R�`�ɕ��z���Ă���Ί挒���̂���t����╪�U���͂��g�p�ł���悤�ɂ��v����B������ɂ���A���b�J�[�g�X�P�[���̋L�q���v�ɁA�P�ɉ̕p�x�����łȂ��A���ρA�W�������̏��������A�f�[�^��ǂݎ��₷���Ȃ�̂ł͂Ȃ����낤���B
2.10�ɂ�����
�e�L�X�g�� (p. 12) ��nominal or categorical variable�Ƃ����\�������������Anominal�Acategorical�`�Ƒ����ėǂ����ǂ����ɂ��Ċm�F���s�����Bnominal�̒�`�ɂ�numbers distinguish among the categories�Ƃ��邱�ƁA���̑���categorical���g�p����Ă��Ȃ����Ƃ���A���̕����ł͓��`�Ƃ��Ďg�p����Ă���ƌ��_�t�����B
3.2�ɂ�����
Tukey (1977) �̊ϑ��l�̍��v���@�ɂ��āA���{�l�ɂ͐��̎���5�܂Ő�������@������̂ŁA����Tukey �ɕ키�K�v�͂Ȃ��Ƃ����B
3.4�ɂ�����
polygons (�p�x���p�`) �Ɛ܂���O���t�̈Ⴂ�ɂ��Ęb���������B�p�x���p�`�ł́A�ϑ��l0�̕���݂��邱�Ƃɂ���āA����X���ƌ����悤�ɂ��Ă��邽�߁A�ŏI�I�ɑ��p�`���o���オ�邪�A�܂���O���t�ł͊ϑ��l������Ƃ��납��n�܂邽�߁A���p�`�ɂ͂Ȃ�Ȃ��̂ł͂Ȃ����A�Ƌc�_�����B
3.5�ɂ�����
�������͓��ɏd�v
���`�ϐ���p����̂ł���A���ꂼ��̐����A�����Ă��邱�Ƃ����肷��p�x���p�`��misleading�ł��邽�߁A�q�X�g�O����
(bar chart) �̕����]�܂����B�Əq�ׂ��Ă���B����܂ŁApretest�̓��_��posttest�̓��_�Ƃ����悤�ɁA�A�����̂Ȃ����_���m�ł����Ō���ł������A���Ō��ԕK�v���Ȃ��A�������͖_�O���t�̕����K����ꍇ������̂ł͂Ƃ����c�_�ɂȂ����B
3.8�ɂ�����
�p�[�Z���^�C�����ʂ𐳊m�ɏo���ꍇ�ɂ� (n +0.5) / N * 100 �Ƃ����v�Z����p���邪�A0.5�𑫂��͖̂ڕW�Ƃ���l�����傤�ǒ����ɗ���悤�ɁA�Ƃ����Ӗ������邱�Ƃ��m�F�����B
�y����Ɍ����āz
�E�a����a���̘_���ł����v��@�ɂ��Ċw�ԋ@���݂��Ă��ǂ�
�E�G�N�Z����p����BOX��p�����O���t��A�����̎�ނ̃O���t��1�Ɋ܂߂�
(e.g., �_�O���t�ƃZ���O���t�����킹��) ���@�����K�������Ƃ�����]���������B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i����A����j
�y�[�W�g�b�v�ɖ߂�
2007/05/11�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
Chapter 4 (pp. 49-65).
Measure of Central Tendency
4.1 Introduction
�����U�̒��� (central tendency) ��\������3�̎�v�ȕ��@: (a) mean (���ϒl), (b) median (�����l), (c) mode (�ŕp�l).
�������̕��@�͈قȂ�T�O�������A�قȂ�v�Z���@���g�p����B
4.2 �ŕp�l
���ł��p�x�̍����f�[�^ (���_��ϑ��l) �̒l�Bnominal scale�����f�[�^ (���I�ȕ��ނɎg�p����l��J�e�S���[�ϐ�) �ɂ��g�p���鎖���\�B(e.g., 195���̐g�����������}4.1�ɂ��A34�����܂�68"���ŕp�l�ƂȂ�B�����crude mode�ƌĂԁB�܂��A���ނ�260-279�̂悤�ȕ������ꍇ�Acrude mode��270�ƍl������B)
���ŕp�l��nominal variables�������Ƃ��ɖ𗧂B�������A���_�̕��̓�{�ȏ��n���Ȃ��ꍇ�ɂ͖𗧂��Ȃ��Bn�����Ȃ��ꍇ�A�ŕp�l�͖��m�Ɍ���Ȃ��ꍇ������ (e.g., 268, 273�̗������ŕp�l�ƂȂ邱�Ƃ��l�����邪�A�����ƃf�[�^�𑝂₷���ƂŁA�ŕp�l��270�ƂȂ邩������Ȃ��B)
���ŕp�l���قȂ闣�ꂽ��_�ɂ���ꍇ�Abimodal distribution�ƌĂԁB���̏ꍇ�Amajor mode��minor mode�ɕ������B
4.3 �����l
�����U��50�p�[�Z���^�C�� (���̃|�C���g��艺�Ɋϑ��l�̔������܂܂��) �������B����āA�����l�̏㉺�ɂ͓����̃f�[�^���܂܂�邱�ƂɂȂ�B�f�[�^����ł��菇�ʕϐ��̏ꍇ�A�����l�͐^�̒l���w���B����A�f�[�^�������̏ꍇ�A�����ɋ߂��l2�̐^���w�� (e.g., (9+11)/2 =10)�B
��raw data�������Ȃ����A�}4.1�Ɏ������悤�ɕ��ނ���Ă���ꍇ�ɂ́A�S�̂̃f�[�^�� (N = 192) ����^�̐l (n = 192/2 = 96) ���܂܂��敪��I�Ԃ��Ƃ��ł���B�X�ɁA���̋敪�̒��ɂ������̐l (n = 34) ���܂܂�Ă���ꍇ�ɂ́A���傤��96�ƂȂ�l���v�Z���邱�Ƃ��ł��� (�v�Z��4.1)�B
�������l�͘A�����鐔�l�������A���ʂŎ�����ꍇ�ɗp���邱�Ƃ��ł��� (ordinal, interval, ratio scale of measurements)�B
4.4 Summation Notation
��sigma (��) �Ŏ������B
��in = 1Xi = X1 + X2 +���+ Xn (�v�Z�� 4.2, p. 53)
4.5 ���ϒl
��average��median���������Ƃ����邽�߁A������h�����߂ɂ�mean���g�p�����ق����ǂ��Bnominal variable�Ɏg�p���Ȃ��B
��X�o�[�Ŏ����B
X�o�[ = ��iXi / n (�v�Z�� 4.3, p. 53)
4.6 More Summation Notation
���e�f�[�^�����{�� (C�{) �ɂ������̍��v (�v�Z��4.4, p. 54)
�e�f�[�^�ɂ���l (C) �𑫂�����̍��v (�v�Z�� 4.5, p. 54)
4.7 Adding or Subtracting a Constant
���萔 (c) ���e�f�[�^�ɉ������ꍇ�A���ϒl��X�o�[ + c, �萔 (c) ���e�f�[�^����������ꍇ�A���ϒl�� X�o�[ - c
4.8 Multiplying or Diving by a Constant
���e�f�[�^�ɒ萔 (c) ���������Ă���ꍇ�A���ϒl��c�{����� (cX�o�[)�B�t�Ƀf�[�^��c�Ŋ����Ă���ꍇ�A���ϒl��c�Ŋ���ꂽ�l�ƂȂ� (X�o�[/ c)�B
4.9 Sum of Deviations
���ϑ��l���畽�ϒl���������l (Xi - X�o�[) ����܂��͕��l�ƌĂԁBn�̊ϑ��l������ꍇ�A�S�Ă̕��̍��v�̓[���ɂȂ�B(�����ƕ��l�͈Ⴄ�悤�ȋC�����܂����H)
4.10 Sum of Squared Deviations
�����ϒl����̕��U���悵���l�̍��v�́A���̒l����̕��U���悵���l�̍��v�������Ȃ��B(least squares criterion�ƂȂ�)
(���ŏ����@�F�@�d��A�������߂�ہA�����l�Ɨ\���l�Ƃ̍��̓��a���ŏ��ɂȂ�\���l�����߂���@���ĂԁB)
����Βl���g�p�����ꍇ�ɂ́A���̓��a�͕��ϒl����ł͂Ȃ��A�����l����̏ꍇ�ɍŏ��ƂȂ�B
4.11 The Mean of the Sum of Two or More Scores
����l�̎҂�k�̃e�X�g (�Ⴆ�Β��ԃe�X�g�Ɗ����e�X�g) �ɉ��Ă���ꍇ�An�l�̎҈�l�ЂƂ�ɑ�k�̍��v�_���o����Ă���ꍇ�̕��ϓ_�́@��kX�o�[k (�v�Z��4.7, p. 56) �ł���B
�����ꂼ��̃e�X�g�̕��ϓ_���ʂɏo����Ă���ꍇ (40�_�A45�_�A65�_) �ɂ́A���ϓ_�̍��v���e�X�g�S�̂̍��v�ƍl������ (40�{45�{65 = 150�_)�B
4.12 The Means of a Difference
���v���e�X�g�A�|�X�g�e�X�g�̓��_�̐L�т��r�������ꍇ�A�P���Ƀv���e�X�g�̕��ϒl (97�_) ���|�X�g�e�X�g�̕��ϒl (104�_) ��������B104 - 97 = 7�_
4.13 Mean, Median, and Mode of Two or More Groups Combines
������ (j��) �̃O���[�v�̕��ϒl�͂��ꂼ��̃e�X�g�̍��v�_���Z�o (X�o�[ * n) ���A���v���An. (= n1+n2+n3�cnj) �Ŋ���Ƃ����P���Ȍv�Z�� (�v�Z��4.9, p. 57)
������A�����l��ŕp�l�̌v�Z�ɂ�raw data���K�v�ł���B
4.14 Interpretation of Mode, Median, and Mean
��mode�͍ł������̃f�[�^������l�Ȃ̂ő�\�I�Ȓl�Ƃ�����B
��median�͊ϑ��l�����l�ł���A�ϑ��l�ƒ����l�̋����̍��v�́A�ϑ��l�Ƒ��̂ǂ̒l�Ƃ̋����̍��v�����������Ȃ�B
��mean�͕��U�̏d�S�ƂȂ�l�ł���B�ϑ��l�ƕ��ϒl�̋����̓��a�́A�ϑ��l�Ƒ��̂ǂ̒l�Ƃ̋����̓��a�����������Ȃ�B
4.15 Central Tendency and Skewness
�����K���z�̂悤��unimodal�ł���A���E�Ώ̂̕��U�̏ꍇ�A���ρA�����l�A�ŕp�l�͈�v����B
��positively skewed distribution�̏ꍇ�A���ϒl�͒����l��ŕp�l�����傫���Ȃ�Anegatively skewed distribution�̏ꍇ�͋t�ɂȂ�Bskewed distribution�̏ꍇ�A�����l�͕��ςƍŕp�l�̊ԂɈʒu����B
��unimodal�ł�⍶�E��Ώ̂ƂȂ�ꍇ�A�����l�ƍŕp�l�̋����́A�����l�ƕ��ϒl�̋�����2�{�ƂȂ�B Mode �� 3(Median) - 2 (Mean)
4.16 Measures of Central Tendency as Inferential Statistics
����W�c���璊�o�����T���v���̌��ʂ����W�c�̌X����\������̂�inferential statistics�ƌĂԁB�ꕽ�σ� (Э�) ��ꕪ�U�̂悤�ȕ�W�c�̖��m���̂��Ƃ�ꐔ�Ƃ����B�ꐔ�̂��Ƃ��p�����[�^�Ƃ������B
���T���v���̌��� (X�o�[) �ƃp�����[�^ (��) �Ƃ̍���sampling error�Ƃ����B
��inferential statistics�ł́Asampling error���ł��������Ȃ镽�ϒl���g�p�����B
(����median���g�p���āAmean�Ɠ�����sampling error�ɗ}�������ꍇ�ɂ́A50%�ȏ㑽���̃f�[�^�����K�v������B)
4.17 Which Measure is Best?
��������1�ł͂Ȃ�
nominal scale�ɂ�mode
���ɂ���l����X�Ȃ铝�v�������\�Ȃ̂�mean
skewed distribution�̏ꍇ�ɂ�median
4.18 Chapter Summary
4.19 Case Study
4.20 Suggested Computer Exercise
�ȗ�
Chapter 5 (pp. 66-79)
Measure of Variability
5.1 Introduction
�����v�I�ɂ����đ�Ȃ̂͒����̒l (central tendency) �ƕ��U (variability�������͋ώ���) �ł���B�{�͂ł�variability�������l�Ƃ��Ďg�p�����range, semi-interquartile range, variance, standard deviation�ɂ��Đ�������B
5.2 The Range
���ő�l�ƍŏ��l�̍��B�������A����outlier�ɂ���ċɒ[�ɕ����L���Ȃ��Ă��܂��̂Œ��ӂ��K�v�B
5.3 H-Spread and the Interquartile Range
���S�̂�100%�Ƃ����Ƃ��ŏ���25%�ɒB����l��first quartile, 50%�ɂȂ�l��second, 75%�ɂȂ�l��third�Ƃ��āAthird quartile����first quartile�̒l���������l (range) ��interquartile range (�܂���H-spread) �Ƃ����B���̒l��������̂�semi-interquartile range�ƌĂ�� (�v�Z��5.1, p. 67)�B
��Md�}Q �Ƀf�[�^�̒����������܂܂��BMd�̑����midhinge (Q1 + Q3) / 2���g�p����ƁAmidhinge�}Q�ɂ��f�[�^�̒����������܂܂��B
5.4 Deviation Scores
��H-spread��semi-interquartile range�͑S�Ă̓��_���܂ނ킯�ł͂Ȃ��̂ŁA�X�̃f�[�^�ɍ��E����ɂ����B
5.5 Sum of Squares
�����ꂼ��̒l�̕����悵�A��������v�����l��sum of squares�ƌĂсA��iXi2�Ŏ����B(�v�Z��5.2, p. 68)
5.6 More About the Summation Operator, ��
����蕡�G�Ȍv�Z�� (�Ⴆ�A�ϑ��l�ɒ萔�𑫂��A������悵���l�̘a���v�Z����ꍇ) �������Ă��� (�v�Z��5.3, p. 68)�B
5.7 The Variance of a Population
�����U�ɕ�W�c�̃f�[�^N�S�Ă��܂܂�Ă���ꍇ�A���̕��U����2�Ŏ��� (�v�Z��5.4, p. 69)�B
���������A���̌v�Z���́A��W�c���璊�o�����T���v���ł���ꍇ (�f�[�^��n�̏ꍇ) �ɂ͎g�p�ł��Ȃ��B
5.8 The Variance Estimate from a Sample
����W�c�̕��U�̓ʂ�p�����v�Z���ɂĎZ�o����̂����z�I�����A�ʂ͖��m���ł��邽�ߎg�p���鎖���o���Ȃ��B
��X�o�[����ʂ𐄒肷�邱�Ƃɂ��Asum of squares�����ۂ����������Ȃ��Ă��܂��B�����ŁAsum of squares, ��i(Xi - X�o�[)2 ��n�����������l�An - 1 (���R�x) (��, ƭ�) �Ŋ���Ƃ�����@���Ƃ��� (�v�Z��5.5, p. 70)�B
5.9 The Standard Deviation
���W�����̓p�����[�^���ЂŎ����A�T���v������̗\����s�ŕ\���B����͕��U (��2�As2) �̕������ł���B
5.10 The Effect of Adding or Subtracting a Constant on Measures of Variability
�����ϒlX�o�[�ƂȂ�f�[�^�Q�ɑ��萔c���������ꍇ�̕��ϒl��X�o�[+ c �ł���B���̏ꍇ�̕��� (Xi+ c) - (X�o�[ + c) = Xi - X�o�[ �ƂȂ邽�߁A���X�̕��ƕς��Ȃ��B���̂��ߒ萔����������������肵�Ă��A���U (range, Q, sum of squares) �ɂ��e����^���Ȃ��B
5.11 The Effect of Multiplying or Dividing by a Constant on Measures of Variability
���萔c���������Ă����ꍇ�ɂ̓f�[�^�̕��ς�cX�o�[�ƂȂ�B���������āAsum of squares�̓�i (cXi - cX�o�[)2 �ƂȂ�B������v�Z����ƁAc2��ixi2 (p. 71) �ƂȂ�B�܂�A���X�̕��U�萔s2 �ɁA�萔�̓��c2������������c2 s2�@���A�萔���������ꍇ�̕��U�ƂȂ� (�v�Z��5.6, p. 72)�B
���W�����͕��U�̕������ł��邽�߁A��c2 s2 = |c| s�ƂȂ� (�v�Z��5.7, p. 72)�B
�����U�͐��ł���A�W�����͕��ɂł��Ȃ��̂ŁA��Βl�Ƃ���B
������c = 1/s �ł���A��c2 s2 = ��(1/s)2 s2�A= 1�@�ƂȂ�B
���萔c�Ŋ������ꍇ�ɂ́A1/c���������̂Ɠ��l�̌��ʂƂȂ�B
5.12 Variance of a Combined Distribution
�����ƂȂ�f�[�^�Q��Ⴆ�Ό��̃f�[�^�� 3, 3, 3, 3��5, 5, 5, 5�̏ꍇ�A���ꂼ��̕��U�̓[�������A���킹���ꍇ�̕��U�̓[���ɂȂ�Ȃ��B�قȂ�f�[�^�Q�����킹��J�̃T���v���̕��U���v�Z����ꍇ�ɂ́A�v�Z�� 5.8 (p. 73) ���g�p����B
5.13 Inferential Properties of the Range, s2, and s
��sampling error�̓T���v�����������قnj�������B���̂悤�Ȑ�����consistency�Ƃ��Ēm����B�S�Ă�sample statistics�͂��̐����������Ă���B
Expected Values and Unbiasedness
���T���v���̕��Us2��unbiasedness�������Ƃ��]�܂����B�܂�A��̂Ȃ��T���v�����O���d�v�B���z�I�Ȃ̂�s2���p�����[�^��2��unbiased estimator�ƂȂ邱�Ƃł���A���̏ꍇ�ɂ�sampling error�̓[���ƂȂ�B���̂��߁A�T���v������̗\���l E (s2) ���p�����[�^��2�ƈ�v����v�Z��5.9 (p. 74) �����藧�B
���T���v����unbiased�ɂȂ邽�߂̐��͏d�v�ƂȂ�Bs�̓Ђ�Ⴍ���ς���X���ɂ�����̂́A����bias�͏��Ȃ��B�Ⴆ��n = 6��5%�ł��邵�An = 20�ƂȂ��1%�ƂȂ�B
��range�̓f�[�^���ɉe�����₷�����A���Us2�̓f�[�^���Ɉˑ����Ȃ��B���������A���Ȃ��f�[�^���ł��f�[�^���������ꍇ�Ɠ����悤�ɎZ�o�����Ƃ����킯�ł͂Ȃ��B
���\5.1�ɃT���v���T�C�Y�ɂ���āA���Ғl���ǂ̂悤�ɕω����邩��������Ă���B
��Range��s2��s�̑�ւƂ��Ăł͂Ȃ��A�⑫�I�Ȃ��̂Ƃ��Ďg�p����邱�Ƃ��]�܂����B
5.14 Chapter Summary
5.15 Case Study
5.16 Suggested Computer Exercise
�ȗ�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i����j
�E �ŕp�l���o�����߂ɂ́A���ސ��~2�ȏ�̐l�����K�v�i�}4.1�̏ꍇ�A���ނ̐���13���邽�߁A26���ȏオ�K�v�ƂȂ�B
�E 4.9�ł̕��i�l�j (deviation, or deviation score) �Ƃ́A���{�Ō������l�Ƃ͈قȂ�B���{�̖͋[�������ł悭�g���Ă�����l�́A���w����v���T-score�iT=50+10z�j�ɑ�������B
�E 5.8
�@ 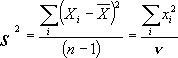 �@�́A�T���v����n�ł͂Ȃ�n-1�i���R�x�j��p���闝�R�́A��W�c�̕��U�ɋ߂��Ȃ�悤�ɂ��邽�߁B���ɃT���v����n���������� n �ŕ���2��̘a������̂� n-1�Ŋ���ƕ��U�����Ȃ�قȂ邱�ƂɂȂ�B�܂�n�Ŋ����Ă��܂��ƕ�W�c�̒l�̂�������������ς����Ă��܂����߂�n-1�Ŋ���B����䂦�ɁA���̕��U�̏o������s�Ε��U�iunbiased variance�Gthe variance of a population estimated from a sample�j�Ƃ��Ă���B�������A�l�����傫���Ȃ�Ȃ�قǁAn��n-1�̈Ⴂ�͔��X������̂ɂȂ�̂łǂ�����g���Ă����܂�ς��Ȃ��B�ꕪ�U�𐄒肷�邽�߂ɁA�ʏ�̓��v�\�t�g��n-1���g�p���Ă���B
�@�́A�T���v����n�ł͂Ȃ�n-1�i���R�x�j��p���闝�R�́A��W�c�̕��U�ɋ߂��Ȃ�悤�ɂ��邽�߁B���ɃT���v����n���������� n �ŕ���2��̘a������̂� n-1�Ŋ���ƕ��U�����Ȃ�قȂ邱�ƂɂȂ�B�܂�n�Ŋ����Ă��܂��ƕ�W�c�̒l�̂�������������ς����Ă��܂����߂�n-1�Ŋ���B����䂦�ɁA���̕��U�̏o������s�Ε��U�iunbiased variance�Gthe variance of a population estimated from a sample�j�Ƃ��Ă���B�������A�l�����傫���Ȃ�Ȃ�قǁAn��n-1�̈Ⴂ�͔��X������̂ɂȂ�̂łǂ�����g���Ă����܂�ς��Ȃ��B�ꕪ�U�𐄒肷�邽�߂ɁA�ʏ�̓��v�\�t�g��n-1���g�p���Ă���B
�E 5.12�ŁA�قȂ�f�[�^�Q�����킹��Ƃ��Ƃ����̂́Araw data���g���Ȃ��ꍇ�ɁA���ʂ����킹�����ꍇ�Ɏg�p����B�����炭�Araw
data��p�����ꍇ�ƁA�قړ������ʂȂ�̂��낤�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�X�{�A����j
�y�[�W�g�b�v�ɖ߂�
2007/05/18
6.1 The importance of the normal distribution
���@���K���z�̓K�E�X���z��normal probability curve�Ƃ��Ă��m���A���v�ɂ����čł���{�I�ŏd�v�ȕ��z�ł���B�{�͂ł́A�W�������ꂽ���_��p���āA�X��O���[�v�̃p�t�H�[�}���X��`�ʂ���̂Ɏg���A�܂����̌�̏͂ł��p������B��x��c�x�ɂ��Ă������B
Historical Background
�� ���K���z�ɂ��Ă̌����́A���Ȃ��Ă�17���I����n�܂����B����1�̂��̂̏d����������Ƃ��ɁA�ϑ������d���͓���ł͂Ȃ����A�\���ȉ��o��Ɗϑ��̕��z�����̃p�^�[���i���Ō������K���z�j�ɂȂ邱�Ƃ��킩���Ă����B���̕��z�́A
�� �ŏ��� "normal curve of errors" �ƌĂ�Ă����B
6.2 God loves the normal curve
���@����덷�ȊO�̊ϑ��ϐ������K���z�i�������͂قڐ��K���z�j�ɂȂ邱�Ƃ����������i�R�C����10���āA�\���o��m���Ȃǁj�B���K���z�ł͕��ϒl�ƍŕp�l�͓���ł���BFigure 6.1�̃O���t�͍��E�Ώ̂łقƂ�ǐ��K���z�ł��邪�A����͑���덷�ɂ����̂ł͂Ȃ��A���R�̖@���ɂ����̂ł���B
���@�ǂ�Ȏ��ؓI�Ȋϑ��ϐ������S�Ȑ��K���z�ɂ͂Ȃ�Ȃ��B�Ȃ��Ȃ�A�ϑ��ϐ��ɂ͊Ԃ�����A�A�����Ă���킯�ł͂Ȃ�����ł���i4��5�̊Ԃɂ�4.5�Ȃǂ������j�B
���@19���I�㔼�ɁA�l�X�Ȋϑ��ϐ��͐��K���z�ɑ�ϋ߂��Ȃ邱�Ƃ������ꂽ�i��FFigure 6.2�j�B�قƂ�ǂ̕ϐ��͐��K���z�ɗގ����邪�A���S�Ȑ��K���z�ɂ͂Ȃ�Ȃ��B�ϐ����̂͐��K���z�ɂȂ��Ă��A�ϑ��ϐ��͊��S�Ȑ��K���z�ɂ͂Ȃ�Ȃ��B�ǂ�Ȃ��̂ɂł�����덷�������邩��ł���B���̌덷�͑��͂ƂĂ����������߁A���ۂɂ͖������邱�Ƃ��ł���B�������v�ɂ����Đ��K���z���d�v������Ă���̂́A���̐��w�I�����̂��߂ł���B���̂ǂ�ȕ��z���A���̂悤�ȓ����͎����Ȃ��B
���@�������A�ǂ��f�[�^�͐��K���z�łȂ���Ȃ�Ȃ��킯�ł͂Ȃ��A���K���z���Ȃ��Ȃ��ϐ�����������i��F�N���A�����ւ̐M�O�j�B
���@���K���z�͑S�āA�R��1�ŁA���E�Ώ̂ŁA�ʁ}�Ђ̂Ƃ����points of inflection�i�J�[�u����ւ��Ƃ���j������A�[�̕�����0�Ɍ���Ȃ��߂Â���0�ɂ͂Ȃ�Ȃ��B
6.3 The standard normal distribution as a standard reference distribution: z-scores
���@�e�X�g��42�_���Ƃ������Ƃ����A���ς�1.5�W��������ł���Ƃ������Ƃ̂ق����A���z�̑��̓��_�Ƃ��ւ��B�W�����ŕ\����链�_�̂��Ƃ�z-score�Ƃ����B�Ⴆ�AIQ�̕��ς�100�ŕW������15�̏ꍇ�AIQ130�Ƃ�z-score��2�Ƃ������Ƃł���i����6.2�j�B
���@�܂�Az-score�͕��ς���ǂꂭ�炢�̕W�������A�ォ���ɗ���Ă��邩�������Ă���B���K���z�ł͂قƂ�ǂ̏ꍇ�A���ς���ǂꂭ�炢�̕W��������Ă��邩��m�肽���ꍇ�������B�����m�邱�Ƃ��ł���A���链�_�Ԃɂ��ẮAstandard normal curve (Appendix��Table A)�����邱�Ƃɂ���ĕ�����B���̃J�[�u�́A�萔�������揜����Ă��ς��Ȃ��B
���@�ǂ�ȓ��_�ł��A���ς�0�A�W������1�̓��_�ɕϊ����邱�Ƃ��ł���B����6.3��Figure 6.3�́A�W�����_�̎���O���t�ł���B
6.4 Ordinates of the normal distribution
���@�J�[�u�̏c���W��m�肽���Ƃ��ɂ́AAppendix A��Table A�ɍڂ��Ă���Bz = 0�̂Ƃ����A�ł������B
6.5 Areas under the normal curve
���@���z�̊����A�܂肠��z���_��艺�ɂ��銄���i���p�[�Z���^�C�����ʁj��m��K�v�����邱�Ƃ������B���̏ꍇ�A���_��W��������Table A����ǂݎ��B
6.6 Other standard scores
���@���̂܂܂̓��_�����A�W��������Ă���ق������߂����₷���B�W��������Ă��链�_�ł́A���ςƕW��������肾����ł���B�����W�����_�Ƃ����B
6.7 T-score
���@T-score�͕W�����_�����A���ς�50�ŕW������10�ł���BT-score��30��������p�[�Z���^�C�����ʂ�2�ʂŁA70��������98�ʂł���BFigure 6.5�ɁAz-score, T-score�⑼�̕W�������ꂽ���_�̊W���f�ڂ���Ă���B
���@�ł́A�Ȃ��p�[�Z���^�C���ł͂Ȃ��W�����_��p����̂��낤���B�Ȃ��Ȃ�A�p�[�Z���^�C���͕��ς⑊�ւɂ͎g���Ȃ����߂ł���B�p�[�Z���^�C�����ʂ�90�ʂ�95�ʂ��ׂ��ꍇ��50�ʂ�55�ʂ��ׂ��ꍇ�ł́A�Ⴂ��3�{�ȏ�ɂ��Ȃ�B�W�����_�ł́A���̂悤�Ȃ��Ƃ��N����Ȃ��Ȃ�B
6.8 Areas under the normal curve in samples
���@���ς�W�������T���v�����琄�肳�ꂽ���̂������ꍇ�ATable A�̒l�͐��m�ł͂Ȃ��u��v�ł���B���́u��v�̒��x�́A�ǂ̂��炢���ς�W���������m�ɐ��肳��Ă��邩�ɂ��B�T���v����100�ȏ゠��A�^��z-score�Ƃ�0.1�ȉ��������Ȃ��ƍl�����A�قƂ�ǂ̏ꍇ�͂���ŏ\���ł���B
6.9 Skewness
���@���S�ɕ��z��`�ʂ���ɂ́A�������X����varaiability�����ł͂Ȃ��A��Ώ̐��̓x������c�x���K�v�ł���B�c�x�𑪒肷��ɂ�2�̕��@������B����positively skewed�ł������ꍇ�A���ς��ł��傫���l�ŁA�ŕp�l�͍ł��������l�ł���BNegatively skewed�̏ꍇ�͋t�̌X���ɂȂ�B
���@Figure 6.6�͗l�X�Șc�x�������Ă���i�W�����_�j�B�c�x���ς��ƁA���ϒl�A�����l�A�ŕp�l�̈Ⴂ�͑傫���Ȃ�BKarl Pearson�ɂ���āA�c�x�����߂���6.6�̎��������ꂽ�B���̏ꍇ�A���͕W�����ŕ\�����A���ςƍŕp�l�̋����ł���B������= .5��������A���ϒl�͍ŕp�l����0.5�W��������ɂ���B
���@�������v�ŗp������ۂɂ́A���̎����C������A�ŕp�l�ł͂Ȃ������l���g����isampling error�������l�̂ق������Ȃ����߁B���ϒl�ƍŕp�l�̈Ⴂ�͕��ϒl�ƒ����l�̈Ⴂ�̖�3�{�ɂȂ�j�B����́A6.7���Ŏ�����Ă���B
���@��1�͂���1�̘c�x�𑪒肷����@�ł���A�������v�ł͂����炪�D�܂��B
���@���܂蕁�y���Ă͂��Ȃ����A���z�̌`���������߂ɁA�����҂͘c�x�̓x�����������ׂ��ł���B
6.10 Kurtosis
���@�����܂ŁA�������X���Avariability�A�Ώ̐������Ă������A4�ڂ̓����͐�x�ł���B���K���z�ŗ\�����������A�ɒ[�ȓ��_�������̂����Ȃ��̂���m�肽���Ƃ��ɂ́A��x���p������i6.9���j�B
���@Figure 6.7�ɂ͕��ς�SD�������ł���3�̍����̕��z�����邪�A�����͕��̐�x�ł���B�������x���ɂ� (platykurtic)�A�Ƃ����B���̂悤�ȏꍇ�ɂ́A���K���z�����A�ɒ[�ȓ��_�����Ȃ��B
���@����A�E���̕��z�ł͐�x�������Aleptokurtic�ƌĂ��i���K���z�ł͐�x��0�ł���Fmesokurtic�j�B�c�x���������z�͐�x�������Ȃ�X��������B
���@��x�͒������X���Avariability�A��x�������ڂ���Ȃ����A��x�͂��铝�v�I�e�X�g�̐��m����]������Ƃ��ɏd�v�ƂȂ�i13�͂ɂāF�M����ԁj�B
6.11 Transformations
���@�f�_�𐳋K���z�ɋ߂Â��镪�z�ɂȂ�悤�ɕϊ�����ꍇ������B���[�g��t���ɂ�����ALog��������肷�邱�ƂŁA��x�����Ȃ��Ȃ邱�Ƃ�����B���̂悤�ȕϊ��́A2�̕ϐ��Ԃ̐��`�Ŗ����W����`�ɂ��鎞������i8�͂ɂāj�BFigure 6.6�ł͕ϊ����邱�Ƃɂ�镪�z�̕ω��������Ă���B
���@�t���ɂ���Ɛ��K���z���Đ�����A��悷��Ɛ��K���z�ɂȂ�B���[�g��Log�ɂ���ƁAFigure 6.6�̏�̐��K���z�ɂȂ�B�]���āA���̘c�x������B���̂悤�ɕϊ����邱�Ƃɂ���āA���K���z���K�v�ƂȂ铝�v���s�����Ƃ��o����B
6.12 Normalized Scores
���@��������ϐ������K���z���邱�Ƃ����肳��Ă���ɂ�������炸�A�ϑ��������̂����K���z���Ă��Ȃ��ꍇ�ɂ́A�ϑ����ꂽ���z�𐳋K�����邱�Ƃ�����B���̕ϊ��͒P���i���Ԃ͈ێ������j���A���`�ł͂Ȃ��B
���@���K�����ꂽ���_��t-score��scale�ŕ\�����B���̓��_���p�[�Z���^�C���ɒ����A���̃p�[�Z���^�C����t-score�ɒ������Ƃɂ���čs����B
6.13 Chapter summary
���@�����̎Љ�I�E�s���Ȋw�I�ȕϐ��͐��K���z�A�������͐��K���z�ɋ߂��Ȃ�B�������v�ł������ł���B���K���z�͍��E�Ώ́A�R��1�A�����Ēޏ��^�ł���Bz-score���ǂ��m���Ă���A�����Table A�Œl���Q�Ƃł���Bt-score������B�܂��A�c�x���x�́A���K���z�Ƃ͈Ⴄ���Ƃ��������̂ł���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�X�{�j
���f�B�X�J�b�V�������R�����g��
�E ���K���z��"normal curve of errors"�ƌĂ�Ă����̂́A�������̂����x���������Ƃ��̌덷���܂l�ɂ�鐳�K���z����������ł��낤���B�قȂ���̂𑪂������K���z�ł�"error"�Ƃ����ꂪ�����Ă���B
�E 6.4�Ɋւ��āA���̒��� 'u'�i���[�j�͏c���W(ordinate)�ŁAX������̍������w���Ă���B
�E �����̃T���v������100�ȏ�ł���A��W�c�̕��ςƕ��U����̐^��z-value�ƁA�T���v�������z-value�̂��ꂪ�������Ȃ邱�Ƃ���A�T���v����100�ȏオ��̖ڈ��ɂȂ邱�Ƃ��킩�����B
�E 6.9�̃��i�I�[���j���O�i�[���j�̂Ƃ����K���z����B
�E 6.9��6.7���Ɋւ��āA�u���ϒl�ƍŕp�l�̈Ⴂ�͕��ϒl�ƒ����l�̈Ⴂ�̂��������R�{�v�Ȃ̂Ŏ��Łu�R�v���|���Ă��邪�A�r�������Ǝv�������A���ςƒ����l�ƕW����������ΊȒP�ɘc�x���Z�o�ł���ǂ�������B
�E 6.10�ł̃�1�͘c�x�A��2�͐�x������킵�Ă���B��x���ɂ��ꍇ�́A��2�͕��̒l�ɂȂ�B
�E 4th root�Ɋւ��Ă̗�j16��4th root�͂Q�ł���B�i2*2*2*2=16�j
�E ��x��c�x�̒l���ǂ̂��炢�ɂȂ�Ɛ��K�������ƂȂ�A�f�[�^�̕ϊ��iTransformation�j���K�v�ɂȂ�̂ł��낤���H�@���ۂ́A�O��l�ƌ����l�������A������x�̃T���v����������A���ɂȂ邱�Ƃ͏��Ȃ����A���Ȃ�c��ł����ꍇ��A2�̏W�c�̕��z��1�����������̘c�x�A��������������̘c�x�̏ꍇ�͖��ƂȂ邩������Ȃ��BSPSS�ŗl�X�ȏꍇ�̃f�[�^�ϊ����\�ŕ֗��������B
�@�ǂꂾ���Ώ̂���c��ł��邩�A���K���z�����E���Ă��邩��z-distribution�Ō�����@�����邪�A������T���v�����������Ƃ��͎��ۂ̃f�[�^�̕��z�����Ĕ��f��������������₷���B�iTabachnic
& Fidell, 2001, p. 73- 90���Q�l�ɂȂ�)
z = Skewness / Std. Error of Skewness�@
z = Kurtosis / Std. Error of Kurtosis
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i����A�C�j
�y�[�W�g�b�v�ɖ߂�
2007/06/01
Chapter 7.
Correlation: Measures of relationship between two variables
7.1 Introduction
�E �u���ցv��2�̕ϐ��̊W���������Ƃɗp������B
�E �����ϐ�X�̓��_���Ⴍ�Ȃ�ƕϐ�Y�̓��_���Ⴍ�Ȃ�Ƃ����ꍇ�ɂ́u���ւ�����v�Ƃ����B���̑��ւ̋�����strong, low, positive, moderate�Ȃǂ̗p��Ŏ������B
�E 2�ϐ��̊W�⌋�т���coefficient of correlation�ɂ���āA���̓x��������������\�����B
7.2 The concept of correlation
�E coefficient of correlation��Karl Pearson�ɂ���čl�Ă��ꂽ�A���ւ̓x�������������l�ŁAr��� (rho, ��W�c�Ɏg�p�����)�Ŏ������
7.3 Scatterplots
�E �U�z�}��p���邱�Ƃɂ��A2�ϐ��̊֘A�̐�����������B
�E �܂��A�Z�o���ꂽr���{����2�ϐ��̊W���W�Ă��邩�ǂ������m�F���邱�Ƃ��ł���B
�E �}7.1�͊��S�Ȑ��̑��ւ������Ă��� (r = 1.00)�B�܂��A�}7.2�͊��S�ȕ��̑��ւ������Ă��� (r = -1.00)�B�������A�����̒l�������͔̂��ɋH�B
�E �}7.3�͕ϐ��Ԃɑ��ւ��Ȃ� (r = 0.00) ��Ԃ������Ă���B
7.4 The measurement of correlation
�E Pearson�̑��W����2�ϐ��̐��`�I�ȑ��ւ̓x���� (magnitude) �ƕ��� (direction) ��ʓI�Ɏ����Ă���B�܂��A���`�ϐ��ȊO�̕ϐ��Ɏg�p�ł���B
�E r�� -1.00����A0��ʂ�A+1.00�܂ł̒l�ŕω�����B
�E ���̒l��p���邱�Ƃɂ��A�ϐ��Ԃ̊֘A�̋�������������r���邱�Ƃ��\�ƂȂ�B
7.5 The use of correlation coefficients
�E ���ʁAGRE�̓��_�A�R�[�X���т�T-score�̊֘A�ȂǁA���W�����ɋ����Ă���B
7.6 Interpreting r as a percent
�E ���W���͒��ڃp�[�Z���g (percentage) �Ƃ��Ĉ������Ƃ͏o���Ȃ��B�������A�W���� (standard deviation) ��standard-score units �ɑ����W����p����ꍇ�ɂ̓p�[�Z���g�Ƃ��ĉ��߂��鎖���\�ł���B
�E �W�����Ŏ������ꍇ�A���W���ɂ́AY (the predicted variable) �̕��ϒl�ƌl�̒l�Ƃ̋����ƁAX (the predictor) �̕��ϒl�ƌl�̒l�Ƃ̋����̔䗦�ł���B�܂�Ar = .60�ł���ꍇ�A�X�̃f�[�^��X�̕��ϒl�̂��狗���ɔ��Y�̕��ϒl����̋����͂���60%�ƂȂ邱�Ƃ����� (e.g., X�Ƃ̋�����100�Ƃ����Y����̋�����60�ƂȂ�) �B
�E ����A1 - r �͕ϐ�X����ϐ�Y���\�������ꍇ�̕��ϒl�܂ł̋����ł���B
7.7 Linear and curvilinear relationships
�E r�̒l�͕ϐ�X��Y�Ƃ̐��`�̊֘A�������Ă���B
�E �������A�U�z�}�������2�ϐ��Ԃ̊֘A���Ȑ��` (curvilinear) �̏ꍇ������B���̏ꍇ�Ar�͕ϐ��Ԃ̊֘A��Ⴍ���肵�Ă��܂� (�}7.4��}7.5B�̂悤�ȏꍇ)�B
�E �U�z�}�����āA���`�������ł͂Ȃ������m�F���邱�Ƃ��d�v�ł��� (�Ȑ��̏ꍇ�ɂ�8.27�ɂ��鑪����@��p����)�B�������A�W�{�������Ȃ��Ɣ��f���o���Ȃ��B
�E �قƂ�ǂ̏ꍇ�A�֘A�͐��`�𐬂��B�������A�V����ʂ⏰�ʌ��ʂ�����ꍇ�ɂ͐��`�ɂȂ�Ȃ� (�}7.5A)�B
7.8 Calculating the Pearson product moment correlation coefficients, r
�E 2�̕ϐ��̕W����sx��sy�A�Ƌ����U (covariance) sxy��������A�s�A�\���̑��W�����Z�o�ł���B�����U��7.1�̌v�Z���ŎZ�o�\ (p. 112)�B
�E �s�A�\���̑��W����7.2�̌v�Z����p���� (p. 112)�B
7.9 A computational illustration of r
�E ��v�Z�ł����������Ă݂邱�Ƃ�E�߂܂��B
�E X��Y�Ԃ̋����U�̌v�Z���͂��V���v���ɂ����7.3 (p. 113) �ł���B
7.10 Scatterplots
�E outliers���Ȃ����ǂ������m�F�����ł��U�z�}���݂邱�Ƃ��d�v�ł���Br�̒l�͐���outliers�ɂ���đ傫���c��ł��܂��B
�E �������Aoutliers�͑S�̓I�ȌX���ƈقȂ邩��Ƃ������R�����Ŏ�菜���ׂ��ł͂Ȃ��B�}7.5B�̂悤�ɋȐ��`�ɂȂ��Ă���ꍇ�A���ꎩ�̂��f�[�^�̐����Ȃ̂ŁA���̂悤�ȏꍇ�ɖ����ɐ��`�ɂ���ׂ��ł͂Ȃ��B
7.11 Correlation expressed in terms of z-scores
�E z-score�Ŏ�����镪�U�����f�[�^�̕W������1�ƂȂ邱�Ƃ���AX��Y��z-score�Ŏ������ꍇ�ɂ�7.4�̎� (p. 116) �����藧�B�܂��A���̏ꍇ�Ar (����) �Ƌ����U�̒l��1�ƂȂ� (�v�Z��7.5, p. 117)�BX, Y�̓��z-score��N�l�S�Ẵf�[�^�œ����ꍇ�A�� = 1�ƂȂ�B
7.12 Linear transformations and correlation
�E X��Y�̒l�̕ϊ� (���Z�A���Z) ��z-score��ω������Ȃ����߁A���W���ɉe�����y�ڂ��Ȃ��B�Ⴆ�A���`�ϊ� (linear transformation) �ƌĂ��P�[�X (X' = aX + b, a����) �ɂ�����z-score�ɂ͉e�����Ȃ����Ƃ��瑊�W�����ς��Ȃ��B
�E ���������āAX��Y�̑��W���͑f�_�Az-score�AT-score�A���̑��̐��`�ϊ���̒l�ŎZ�o���Ă��������ʂƂȂ�B
7.13 The bivariate normal distribution
�E ���ւ̉��߂͐��K���z���ϐ� (bivariate) �̐��K���z�Ƌ����֘A�����B�ϐ�X�̒l���ϐ�Y�̒l�Ƃǂ̂悤�Ȋ֘A�������Ƃ�����ϐ��̊֘A�������̂����ւł���B
�E Bivariate frequency distribution��X�AY�A�p�x (����X��Y�̒l�����f�[�^��) ��3�̑��ʂ������Ă���B
�E �}7.8�̂悤�ɁA�p�x�͍����Ŏ������B
�E bivariate normal distribution�͎O�����𐬂��AX��Y�̑��ւ������Ȃ�قǁA�ޏ��^�͐�x�𑝂� (��increasingly elongated�Əq�ׂ��Ă��邪������������x�������Ȃ�Ƃ������Ƃł��傤���H) (�}7.9)
�E bivariate normal distribution�ɂ͈ȉ��̓���������B (1) X�̂��ꂼ��̒l�ɑ��AY�̒l�̕��U�͐��K���z�𐬂� (�t��������)�B(2) Y�̕��ϒl (Y-means) �Ɨl�X�Ȓl��X���d�Ȃ�l�͒����ƂȂ� (�܂�A���`�W�ɂ���)�B�܂��t�̂��Ƃ�X�̕��ςɂ��Ă������� (������͐}7.11�̂悤�Ȃ��Ƃ��q�ׂĂ���̂ł��傤���H)�B(3) �U�z�}�������U�������B�܂�AY�̒l�̕��U��X�̒l�ɑ��ċϓ��ł���A�t��X�̒l�̕��U�͑S�Ă�Y�̒l�ɑ����ł���B
�E �W�{���������Ȃ邱�Ƃɂ���āA�}7.9�̂悤�ȃX���[�Y��3�����̋Ȑ����`�����B
7.14 Effects of variability on correlation
�E �W�{�̕s�ψꐫ��r�ɑ傫�ȉe����^����B
�E ���肵�������ʈȊO���ώ��ł���ꍇ�A�ϑ��l�����l�ł���ق�r�̒l���傫���Ȃ�B�Ⴆ�A����e�X�g�̎ґS�̂̌��ʂ���W�{�𒊏o�����ꍇ (range restriction���s�����ꍇ)�A�S�̂̒l�ɔ�ׂĒႢ�l���Z�o�����B
�E �}7.11�̑S�̂���ꕔ�����o�����ꍇ (��1) �ɂ͑S�� (��I) �ɔ�גl���������B
7.15 Correcting for restricted variability
�E ����W�c�̑��� (��I) ��X�̕W���� (��I) �ƁA�V�����W�c�̕W���� (��1) ���������Ă���A�V�����W�c�̑��� (��1) ���Z�o���邱�Ƃ��ł��� (�v�Z��7.6, p. 122)�B
�E �������A�v�Z��7.6�̖ړI��r�̒l��restricted��exaggerated variability�̌��ʎZ�o���ꂽ���̂��ǂ����𖾂炩�ɂ��邱�Ƃł���B���̂��Ƃɂ��A���ʂ̉��߂��K�ɂȂ�B
�E �f�[�^�̕s�ψꐫ��rXY�̒ቺ�͕W�{�̒��o�ɂ���ċN����Ƃ͌���Ȃ��B�T���v���ɕ肪����ꍇ�ɂ��N���� (�Ⴆ�A���Z���Ƃ̐��l��IQ�Ɠlj�͂̊֘A�́A��ʓI�Ȑ��l�̌��ʂɂ��Ă͂܂�Ȃ�)�B
7.16 Effects of measurement error on r and the correction for attenuation
�E measurement error�ɂ����r�̒l�͑傫���e������B(���ꂪ���邱�Ƃɂ���Ēl���Ⴍ�Ȃ�)�B�����reliability of coefficients�ɂ���đ���ł���B
�E ���̐M�����W���͂���ϐ���two parallel measures (�Ⴆ�A�������ڂ��x�]���������ʓ��m�̑��ւȂ�) �̑��ւŎ������B
�E �����A�ϐ�X�̐M������ .90�ł���A10%�̕��U��measurement error�ɂ����̂ł���Ɖ��߂ł���B�ϐ�X��parallel measures�̌��ʂ�rXX�Ŏ������B�����A����ϐ�Y�̐M���� rYY�� .00�̂悤�ɒႢ�ꍇ�A���̕ϐ��𑼂̕ϐ�����\�����邱�Ƃ͕s�\�ł���B
�E �ϐ�X��Y��measurement error���傫���Ȃ�قǁA���ւ��Ⴍ�Ȃ�B����������ƁA�ϐ������m�ɑ��肳��Ă���A���ւ������Ȃ�B�܂��A�e�X�g���ڂ������Ȃ�قǁA�M�����������Ȃ�B
�E �ȏ�̂悤�Ȃ��Ƃ���A���ւ̉��߂ɂ����Ă��ꂼ��̃e�X�g�̐M������m�邱�Ƃ��]�܂����B
�E �ϐ���measurement error���܂܂�Ȃ��ꍇ�̑��W���𐄒肷����@��correction for attenuation (���̏C��) �ƌĂԁB���̏C���ɂ͂��ꂼ��̕ϐ�X��Y�̐M�����W���Ƒ��W�����K�v�ł��� (�v�Z��7.7, p. 126)�BrX��Y���͖��m�̕ϐ��������̒l�Ɋ�Â��Đ��肷��l�ł���B�e�X�g�̐M���� (�v�Z���̕���) �����ۂ����Ⴍ���肳��Ă���ꍇ�A����rX��Y���͎��ۂ����������肳��Ă��܂����Ƃɒ��ӂ���B
�E �Ⴆ��MC�`����essay�`���œ������e���s�����Ƃ���A���ꂼ��̃e�X�g���ڂ����Ȃ���������MC�̐M���� (.50) ���Aessay�̐M���� (.39) ���Ⴉ�����B��̃e�X�g�̑��ւ�.38�ƒႩ�����B������v�Z���ɓ����ƁA���ʂƂ���.86�ƍ������ւɂȂ�B
7.17 The Pearson r and magical distributions
�E �ϐ�X��marginal distribution�Ƃ�X�̒l�̕p�x�̕��U�������A�ϐ�Y��marginal distribution��Y�̒l�̕p�x�̕��U�������Ă���BX�����K���z�𐬂��Ă���A���Y���c�x�̍������z�����Ă����ꍇ�ɂ́A�ϐ��Ԃ̑��ւ͒Ⴍ�Ȃ�悤�ɁA���z�̌`���قȂ�قǁA���� (r) �͒Ⴍ�Ȃ�B
�E ���Z����Ȃǂ̐��l�ϊ��������ꍇ��r�ɂ͂قƂ�lje�����y�ڂ��Ȃ����Ƃ���A�ϐ�X�ƁA�����ϊ������lX'�Ƃ̑��ւ͔��ɍ��� (�قړ�����) �Ƃ�����B
7.18 The effects of the unit of analysis on correlation: Ecological correlations
�E �����̕��ޒP�� (school, cities, states, etc.) �̏W���ł���ϑ��P�ʊԂ̑��ւ�ecological correlation�ƌĂ�邱�Ƃ�����B���ꂼ��̒P�ʂ̕��͂ɂ���āA�ϐ��Ԃ̑��W�������I�ɕω����邱�Ƃ�����B
�E �Ⴆ�Γ����l (�f�[�^) �ɑ��Acity��school district�̂悤�ɈقȂ镪�ޒP�ʂ��p����ꂽ�ꍇ�A���ꂼ��ɂ���ĕϐ��Ԃ̑��ւ��قȂ�B���̂��߁A���ʂ̉��߂͂ǂ̒P�ʂ��p����ꂽ���ɂ���Č��肳���ׂ� (�p�����P�ʓ��ɂ��Ẳ��߂ɗ��߂�ׂ�)�B
7.19 The variance of a sum
�E ��ȏ�̃f�[�^�̓����������ꍇ (X + Y)�A���̕��U��W�����͂ǂ̂悤�ɂȂ邩���v�Z��7.8 (p. 128) �Ɏ����Ă���B
�����v�̕��U = (X�̕��U) + (Y�̕��U) + 2(X��Y�̋����U)
�E ����X��Y�����S�ɓƗ����Ă���ϐ����m�ł���A�P����
�����v�̕��U = (X�̕��U) + (Y�̕��U) �ƂȂ�
�E 3�̕ϐ��̍��v��p����ꍇ�ɂ�
�@�@�@�@�@�@�@�����v�̕��U = (X�̕��U) + (Y�̕��U) + (Z�̕��U) + 2(X��Y�̋����U) + 2(X��Z�̋����U) + 2(Y��Z�̋����U)
�E 4�ȏ�ɂȂ����ꍇ�ɂ���L�̌v�Z���ɑ����Ă����悢�B
7.20 The variance of a difference
�E X��Y�̒l�̍���p����ꍇ�A���U�͌v�Z��7.11�ŎZ�o����� (p. 129)�B
�E 2�ϐ� (X�AY) �̑��ւ͓�̒l�̍����������Ȃ�قǍ����Ȃ�B
7.21 Additional measures of relationship: The Spearman rank correlation, rranks
�E ���ʕϐ� (rank) ��p����ꍇ�A���ʂ̐��ɊW�Ȃ��A�������̃T���v�����܂܂���rranks�Ƃ��ĎZ�o�ł���B
�E ���ʕϐ���p���邱�Ƃ�outlier�̉e����r�̂Ƃ��ɔ�ׂď������Ȃ�B
�E X��Y��2�ϐ����ǂ�������ʕϐ��œ����� (�^�C) ���܂܂�Ă��Ȃ���Ε��ς����U�������ł��邽�߁A���Ƃ̓y�A�̐�n�ɂ���Ēl�����肷��BDi��i�Ԗڂ̃P�[�X�ɂ����鏇�ʂ̈Ⴂ�������Ă���B�v�Z��7.12 (p. 130)�B
�E �����ʂ��܂܂�Ȃ��ꍇrranks��r�Ɠ������A�����ʂ��܂܂��ꍇrranks��r�ƈقȂ���̂́A�قƂ�Ǔ����ł���B
7.22 The phi coefficient: Both X and Y are dichotomies
�E �C�`�[���̂悤�ȓ�i�@�̃f�[�^�ŎZ�o����Pearson product-moment coefficient��phi coefficient�ƌĂ�Ar�ӂ̓ӂŎ������B
�E px��X�ɂ�����1�ł������l�̊����Ƃ���ƁAqx��X�ɂ�����0�ł������l�̊����ł���A1 - px�ł���B�܂��ApY��Y�ɂ�����1�ł������l�̊����Ƃ���ƁAqY��Y�ɂ�����0�ł������l�̊����ł���A1 - pY�ł���B������O���ɂ����ƁA���ւ̌v�Z����7.13 (p. 132) �̂悤�ɑ㐔��p�������Ŏ������B
�E �����ɏœ_�ĂȂ��ꍇ�ɂ�contingency table (�\7.7) ���g�p���鎖���ł���B�\�Ɏ������悤�ɁA���ꂼ��̃Z����a, b, c, d�Ŏ�����Ă���B���̍ہApx = (b + d) / n, pY = (a + b) / n, pXY = b / n�Ƃ���B�����p�����v�Z����7.14 (p. 133) �ƂȂ�B
�E r�ӂ̐��̒l�́AX�ɂ�����1�ł������l��Y�ɂ����Ă�1�̌X���������Ƃ������Ƃ������Ă���B���̒l�͐�Βl1���ł��������l (px��pY�������ł������ꍇ) �Ƃ���B
���f�B�X�J�b�V����&�R�����g��
�E 7.6�ł�standard-score units�́A�W�����������_�̂��ƁB
�E 7.6�ł́A�Ȃ�Y�̕��ϒl����̋�����X��60%�ɂȂ�̂��낤���Br = .60�ł���AX�̒l�́}40%�̒l���Ƃ�ƍl����ꂻ���i�܂�AY��X�̒l��60%��������140%�ɂȂ�̂ł͂Ȃ����j�B
->���W���́A�x�Ƃw�������P�ʁi�W�����̒P�ʁj�Ō���ƁA�x�̕��ς���̋����Ƃw�̕��ς���̋����̔��\���Ă���̂ŁA��=.6�Ȃ�AX��1.0���ς��痣��Ă���Ƃ���Ƃx�͕��ς���.60����Ă���W�ɂ��邱�Ƃ�\���B����āA�x�͂w�̒l��60%�̒l��\���A140%�̊W�ɂ͂Ȃ�ȁB
�E 7.13��elongate�́A��x�������̂ł͂Ȃ��A�����L����Đ�x��������i��r�I����ɂȂ�j�Ƃ������ƁB
�E 7.16�̊��̏C���̕����́A2�̃e�X�g�������\�͂𑪒肵�Ă��邱�Ƃ��O��Ȃ킯�ł͂Ȃ��B�Α��ւƊ��̏C���̋�ʂ���������ƍs�����B�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�\�����̏C���Ɋւ��āA�M�����̒Ⴂ�f�[�^�͑���덷�i�덷���U�j���傫�����Ƃ��Ӗ�����B���̌덷�������f�[�^���m�ő��ւ����ƁA��ѐ��̂Ȃ��덷�ƌ덷�Ƃ̑��ւ͒ʏ�[���ł��邩��A���̌덷�������܂܂ꂽ�f�[�^���m�̑��W���́A���R�A���ۂ̑��ւ������܂�Ⴂ�l��������B������A���Ƃ����B���W�������^�̑��ւɋ߂Â��邽�߂ɁA
���̏C�������F 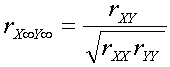 �@�����邪�A
�@�����邪�A
���ۂ͏C���������W������Ă���_���͔��ɏ��Ȃ��l�I�ɂ��قƂ�ǎg��Ȃ��B�ȑO�A���̏C�����s���ƁA�C�����ꂽ���ւ����Ƃ̑��W�����͂邩�ɍ����Ȃ�A���߂ɍ��������Ƃ�����B
�@���W���Ȃǂ̐M�����W���́A�^�̒l�̉����l����邽�߁A�܂�����̕�������ۂ��Ⴂ�l��������̂ŁA�C�����ꂽ���ւ�1�ȏ�ɂȂ邱�Ƃ�����Ɗw���Ƃ�����B�����ŁA���̏C�������Ȃ���Ȃ�Ȃ��قǒႢ�M�����W�����o���Ƃ��́A����ȏ�̕��͂�������A�܂��M�����̂���f�[�^���W�߂邱�Ƃ��挈�ł͂Ȃ����B�����A���̌����ŏC�������ꍇ�A�C���O�ƌ�̑��W������邾���łȂ��A�Q�f�[�^�̐M�����W������сA�ǂ̂悤�ȕ��@�ł��̐M�����W�������Ȃǂ�����ׂ����Ǝv���B
�@���̊��̏C�������́A��e�X�g��I�Ԉ�̖ڈ��ɂ���̂ɗL�p���Ɠ����g�p�����e�L�X�g�ɂ���B�iAllen, M. & Yen, W., (1979). Introduction to measurement theory. Waveland Press, Inc.�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i����A�X�{�j
�y�[�W�g�b�v�ɖ߂�
2007/06/22�@�@�㔼��8�͂͂�����
7.23 The point-biserial coefficient
��1, 0�f�[�^�̂悤��2�l�̕ϐ����A���ϐ��Ƒ��ւ����ꍇ�Apoint-biserial correlation coefficient (rpb) ���Z�o�ł���BY��A���ϐ��AX��1, 0�̕ϐ��Ƃ����ꍇ X = 1�̐l (n1) �̕��ϓ_��Y1�o�[�AX = 0�̐l (n0) �̕��ϓ_��Y2�o�[�Ƃ��āA�v�Z��7.15 (p. 134) �ŎZ�o����Bn1= n0�̏ꍇ�A�v�Z��7.16�����藧�B
7.24 The biserial correlation
��2�l�̕ϐ�X �����X�͐��K���z�����肳���ꍇ (��: ���i�E�s���i�Ƃ���2�ړx�����A���ۂ͂Q�l�ȏ�ɂł���ꍇ)�Abiserial correlation coefficient (rbis) ���Z�o�ł���B���̍ہA�v�Z��7.17 (p. 135) ���g�p���鎖���ł���B���̌v�Z���Ɋ܂܂��u�́Ap = n0 / n. �̏ꍇ�̐��l��Table A����ǂݎ�������l�B
���������Arbis��r�𐄒肷����̂ł���Arpb�̂悤�Ɏ��ۂɊϑ����ꂽ�f�[�^�̊W���������̂ł͂Ȃ��B���̌W���́A���̌W���ƈقȂ�A-1�ȉ��� +1�ȏ�̒l�ƂȂ�ꍇ������B���̂悤�Ȓl���Ƃ�ꍇ�ɂ́AY�̒l�����K���z�𐬂��Ă���Ƃ������肪����Ă���ꍇ��sampling error���������ꍇ (n�����Ȃ�����ꍇ) ������B���f�[�^����100�ȏ�̏ꍇ�A��萳�m�ȑ��ւ��ł�B
���܂��AX�̑f�_�����K���z�łȂ��ꍇ��A�ϐ��Ԃ̊֘A�����`�ł͂Ȃ��ꍇ�ɂ��Arbis��r�Ƃ̊Ԃɂ� .2���x�̈Ⴂ������ꍇ������B
7.25 Biserial versus point-biserial correlation coefficients
��rpb��rbis�͌v�Z��7.18���g���ē������邱�Ƃ��ł���B
�����̏ꍇ�A���[�g�̒l���Œ�1.25�Ȃ��ƂȂ�Ȃ��B�܂�Arbis ? 1.25rpb�ƂȂ邱�Ƃ���Arbis��rpb����25���ȏ�傫���Ȃ�B
7.26 The tetrachoric coefficient
���ϐ�X��Y�̗��������K���z���Ȃ��f�[�^��2�ړx�ɕϊ��������̂̏ꍇ�Atetrachoric correlation coefficient (rtet) ���Z�o���邱�Ƃ��ł���B (��: �ϐ�X = �}���t�@�i�̍��@���Ɏ^�����ǂ����A�ϐ�Y = ����̍��@���Ɏ^�����ǂ����̂悤�ɁA���ۂɂ͎^���E���̓x�����������������ăO���C�]�[��������悤�ȏꍇ) �B�v�Z��7.19 (p. 137) ��p����B�v�Z������a, b, c, d�͊e�Z���Ɋ܂܂�鐔�������Ă���Bux, uy�̒l��Table A���Q�Ƃ���B
��rbis�Ɠ��l�ɁA���ꂼ��̕ϐ��̐��K�������藧���A�ϐ��Ԃɐ��`�̊֘A�����邱�Ƃ����肵�Ȃ���Ȃ�Ȃ��B���f�[�^����400�ȏ゠���萳�m�Ȓl���ł�B
7.27 Causation and correlation
��2�ϐ��Ԃɑ��ւ�����ꍇ�ł��A���̕ϐ��ԂɈ��ʊW������Ƃ͕K�����������Ȃ� (��: ��l������̖{�̐��ƁA�ފw�҂̐��̊Ԃ̑���)�B
�E���ʊW������悤�ȕϐ��Ԃł������Ƃ��Ă��A���W�����������X��Y�������N�����Ă���̂��A���̋t�Ȃ̂����q�ׂ��Ȃ� (��: �s�����e�X�g���ʂ���������̂��A�����e�X�g���ʂ����悤�Ȑ��т̐��k�̕s���������Ȃ�̂�������Ȃ�)�B
�E��3�̕ϐ�����݂���2�ϐ��Ԃɑ��֊W�ݏo���Ă��邱�Ƃ����� (��: ��q�֎Q������Ǝ����̐������̊Ԃɂ́A�ƒ�ɂ����鋳�炪�e�����Ă���)�B
�E1�̌��ʂ�������v����1�ɍi����ꍇ�͋H�ł���A���̏ꍇ�ɂ͗l�X�ȗv�������G�ɉe�����Ă���B
Zero Correlation and Causation
�����̑��ւ�����ꍇ�ɂ����ʊW���ؖ�����Ȃ��悤�ɁA���W�����[���̏ꍇ�ł���̕ϐ��ԂɈ��ʊW���Ȃ��Ƃ͌����Ȃ� (��: �e�X�g�̐��тƊw�K�������Ԃ̊Ԃ̑��ցA���]�����Ȑ��k�͎��Ԑ������Ȃ��Ă��ǂ��Ȃǂ̗v��������)�B�������ꂽ�������s�����Ƃň��ʊW�����ł���B
Negative Correlation and Causation
�����̑��ւ��������ꍇ�ł����Ă��A���̒��ړI�Ȉ��ʊW�̉\�����������̂ł͂Ȃ��B(1000���̐l�̑̏d�̑��茋�ʂƁA�ŋ߈��W���[�X10�{�̂����A�_�C�G�b�g�����͉��{�ł��������Ƃ����₢�̌��ʂɕ��̑��ւ��������Ƃ��Ă��A�_�C�G�b�g���������ނ��Ƃő̏d��������Ƃ͂����Ȃ��B)
�ȏ�̂��Ƃ��ӂ݂�ƁA���W��������ʊW�����߂���̂͊댯�ł��邱�Ƃ�������B
7.28 Chapter Summary
�����ւ̓x�������������l�ŁAr��� (rho, ��W�c�Ɏg�p�����)�Ŏ������
��r�� -1.00����A0��ʂ�A+1.00�܂ł̒l�ŕω�����B
��2�ϐ��Ԃ̊֘A���Ȑ��` (curvilinear) �̏ꍇ������B���̏ꍇ�Ar�͕ϐ��Ԃ̊֘A��Ⴍ���肵�Ă��܂�
���U�z�}�����āA���`�������ł͂Ȃ������m�F���邱�Ƃ��d�v�ł���
��X��Y�̒l�̕ϊ� (���Z�A���Z) ��z-score��ω������Ȃ����߁A���W���ɉe�����y�ڂ��Ȃ��B�Ⴆ�A���`�ϊ� (linear transformation) �ƌĂ��P�[�X (X' = aX + b, a����) �ɂ�����z-score�ɂ͉e�����Ȃ����Ƃ��瑊�W�����ς��Ȃ��B
�����������āAX��Y�̑��W���͑f�_�Az-score�AT-score�A���̑��̐��`�ϊ���̒l�ŎZ�o���Ă��������ʂƂȂ�B
�����ւ̉��߂͐��K���z���ϐ� (bivariate) �̐��K���z�Ƌ����֘A�����B�U�z�}���m�F���邱�ƁB
�����ʕϐ� (rank) ��p����ꍇ�A���ʂ̐��ɊW�Ȃ��A�������̃T���v�����܂܂���rranks�Ƃ��ĎZ�o�ł���B
�����ʕϐ���p���邱�Ƃ�outlier�̉e����r�̂Ƃ��ɔ�ׂď������Ȃ�B
���C�`�[���̂悤��2�ړx�̕ϐ����A���ϐ��Ƒ��ւ����ꍇ�Apoint-biserial correlation coefficient (rpb) ���Z�o�ł���
��biserial correlation�̎Z�o�ɂ́A���Ƃ��Ƃ̃f�[�^�̐��K�����d�v�ł���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i����A����j
���f�B�X�J�b�V����&�R�����g��
�Epoint-biserial correlation (�_�o��)��biserial correlation�i�o�ցj�͗ǂ����Ă��邪�A�_�o�ւ͎��ۂ̊ϑ��f�[�^���m�̑��ւł���̂ɑ��A�o�ւ͐��葊�ւł���B
�E�_�o�W���́A�Ⴆ���ꂼ��̍��ڂ� 1,0�̂悤��2�l �f�[�^�Ƃ��̃e�X�g�����_�Ƃ̑��W�����w���B
�E�o�W���́A�A�������f�[�^�x�Ɣw��ɐ��K���z�����肵��2�l�f�[�^�w�Ƃ̃s�A�\���ϗ����ւ̐���l�ł���B�Ⴆ�A�j���̂悤�ɂQ�l�ȏ�ɂł��Ȃ��f�[�^�ł͂Ȃ��A���ۂ�2�l���ׂ����ړx�ɂ��A����ɍL�͈͂Ƀf�[�^���W�߂�ΐ��K���z������ł���B�����w��ɐ��K���z�����肷��Ƃ����B���̂悤�ɐ��K���z�����肵��X�ƁAY�Ƃ̑��ւ͂ǂ��Ȃ邩�𐄒肵���W�����o�W���ł���B
�@���R�A�_�o�ւ�o�ւ�������A���̍��ڂ́A�����_�Ƀv���X�Ɋ�^���Ă��邱�ƂɂȂ�̂ŁA�ٕʗ́i�܂��͎��ʗ͂Ƃ������j�̂��鍀�ڂƂ�����B����䂦�A�ٕʗ͂̈�̎w�W�ƂȂ�B��͂ǂ̒��x�ٕ̕ʗ͂̂��鍀�ڂ��g�p���������ɂ�邪�Arpb = .2 ���� .3��cutoff point�Ƃ���ꍇ�������悤���B�����̑��ւ��l�K�e�B�u�ȏꍇ�́A���̍��ڂ��A�����_�Ƀ}�C�i�X�Ɋ�^���Ă��邾���ł͂Ȃ��A�܂������ʂ̂��̂𑪒肵�Ă��邩�f�[�^�̓��̓~�X�̉\��������B���̂��߂ɁA�Ⴆ�A���ډ������_�iIRT�j�̕��̓\�t�g�ł���BILOG-MG�ł́A�_�o�ւ�o�ւ̗������Z�o����A�o�ւ�-0.15��肳��ɑ傫���}�C�i�X�̐��l�ł���AIRT���͂���͂����o���Ă��܂��B
�@���̂悤�ɁA�Q�l�f�[�^�̔w��ɐ��K�������肵�Ă��邽�߁A�����A�A�������f�[�^�ł���ΐ��K���z�ɂȂ�ł��낤�f�[�^�����i���Ȃ��Ƃ�����ׂ�100�ȏ�j�������قǁArpb�̒l�͂�萳�m�Ȑ���l�ɂȂ�B���̂��߁A�T���v���������Ȃ��ꍇ��rpb�͒Ⴂ���葊�W�������͂����o���Ȃ��B
�Etetrachoric coefficient�́A���q���͂̔w��ɂ�����̂ɂ��Ă��g�p�\�ł���炵���i���̑��W�����f�[�^�̔w��ɐ��K���z�����肵�Ă���B�j
�E�Ō�̒��ӓ_�̕����ɂ����āA���W��������ʊW�����߂���̂͊댯�Ə����Ă��邪�A�������A���ւ��炵�����ʊW�������Ȃ�����������̂ł́B���̏ꍇ�A�ǂ�����悢�̂��낤�B���Ӑ[�����߂��s���A�ǂ��悤�ȋC������B�܂��A�u���ց����ʊW�ł͂Ȃ��v�ƌ������Ă��܂����Ƃɑ��Ă��A��a�����o����B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i����A�X�{�j
Chapter 8 (pp.152- )
�{�͂ł́A������\�����邽�߂ɑ��ւ��g�p���邱�Ƃ���ȏœ_�Ƃ���B��A�͒ʏ�\�������ϐ��������ړx�A�Ԋu�ړx�A�䗦�ړx�ł��鎞�Ɏg�p���铝�v��@�ł���B
8.1 ��A���̖͂ړI�ipurposes of regression analysis�j
�E���v��@�ɂ��A�Q�ȏ�̓Ɨ��ϐ�����]���ϐ��𐳊m�ɗ\�����邱�Ƃ��\�ɂȂ�B
�E���ʊW�͕s�v�����肵�Ȃ��Ă��悢�i���ʊW�͗\���Ƃ͕ʖ��j�B
�E���ւ��Ⴏ��ΒႢ�قǁA�덷�͈͍̔͂L���Ȃ�B
�E��̓Ɨ��ϐ�(X)����A���]���ϐ�(Y)��\��������`��A�����舵���B
8.2�@�\������ (The regression effect)
�Er = 1.0���邢�� r = -1.0�łȂ�����A�w����̂x�̗\���͂��ׂĕ��ϒl�Ɍ����ĉ�A����B�܂�A�\�������x�̃p�[�Z���^�C���l�͂w�̃p�[�Z���^�C���l����50�ɋ߂��Ȃ�B
�E�}8.1����A���ʂ̗L���Ȑ}���i�}�Q�Ɓj
�E�w�Ƃx�̎��ӕ��z�Ɏg�p�����v�Z���@�́ATukey�̂��̂Ɠ����B
�EX�Ƃx�͂��ꂼ��rx�Ƃry�Ƃقړ������A���ϐ��͕W�{�덷�������������ꍇ�ɐ��K���z����悤�ł���B
8.3�W��z�X�R�A�Ŏ�������A������(The regression equation expressed in standard z-scores)
�E���v�I�ɉ�A���ۂ�������邽�߂̗��_�I�ɂ����Ƃ����߂�����@�͂w�Ƃx��z-score�Ƃ��Ď����ꍇ�ɂ���B
�E��8.1�Q��
8.4 ��A�������̗��p(Use of regression equations)
�E��A�������̖ړI�͊��ɂ���T���v���ɂ�錋�ʂɊ�Â��ĐV�����T���v���̗\�������邱��
�E�����I���T�O�I�ړI�Ƃ��ẮA��A�Ɨ\����z-score�̊ϓ_�Ř_������B
�E���p�I���p�Ƃ��ẮA�w�̊ϑ��l����raw score�̂x��\�������A��������p������������������B
8.5 �f�J���g���W(Cartesian coordinates)
�E���̍��W�́A1�g�̐�(X,Y)�ł�����|�C���g�̓��肪�\�ɂȂ�悤�ɖʂ���悷���i�B
�E���W(0,0)�@���@X����Y������������_�B�i��F�}8.2�Q�Ɓj
�E���W�ʂ̂����Ȃ钼�����P���ȕ������Ŋ��S�ɕ\�����Ƃ��\�B�i�}8.2�ł́AY = .5X+1�j
�E������\����ʓI�ȕ������F Y = bX + c�@�iY��\�����邽�߂�X�̐��`�ϊ��j
8.6 Estimating Y from X: The raw-score regression equation
�E�Ɨ��ϐ�X����]���ϐ�Y��\�������������ɂ́AX��Y�̑��ւ���ї��ϐ��̕��ς�SD���K�v�B
�E�ŏ�����i���j�@�ɂ��A��A�����������Ă�B�i��8.2�`��8.2B�j
�E X�o�[��Y�o�[�� �̌�_�͉�A������Ɉʒu���A�����Ȃ���W��\����A������r�l�ɂ�����炸(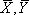 )��ʉ߂���B
)��ʉ߂���B
8.7 �����덷(Error of estimate)
�EX����Y�𐄑�����ۂɌ덷��������̂ŁA�\���l�����ۂ̊ϑ��l�ƈ�v���邱�Ƃ͂܂�
�E��8.3�F�c����i�Ԗڂ̐l�ɂ���X����Y��\������ۂ̌덷���ϑ��lY�|�\���l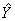 �iY�n�b�g�j
�iY�n�b�g�j
�E�c�������̒l���ϑ��l �� �\���l
�E��A�������͂��݁A�㕔��score�F���̎c���A������score�F���̎c��
8.8 ����W���E��^��(Proportion of predictable variance, r^2)
�E�\7.3�̖ړI�́AX��������ł���Y�̕ϓ��̊���.
�E�ϑ��lY�A�\���l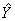 �͓����U�Ŏc���̕��ς͂O�B
�͓����U�Ŏc���̕��ς͂O�B
�E�ϑ��lY�̕����a�{�c���̕����a���ϑ��l�̑������a �@�i��8.4�j
�E��A�������ɂ������ł���Y�̕ꕪ�U�̊��� �@�i��8.5�j
�E�����ł��Ȃ��i�\���ł��Ȃ��jY�ɂ�����ϓ��̊��� �@�i��8.7�j
8.9 Least-squares criterion
�E�c���̕����a���ŏ��ɂȂ�悤��b�����c���߂�B
�E�ŏ�����@�͗����������A�������v�w�ł͍D�܂�邪������ł́A���̕��@���D�ʂȏꍇ������B
�E���̕��@�ł́A��A������mean�ł͂Ȃ�median���g�p�����Bmedian��A�����͗e�ՂɎZ�o�ł��邪�A�ŏ�����@�Ɣ�r����ƃT���v�����O�덷�������₷���B
�E��8.2��b,c�ɂ��AX��Y�̎U�z�ɂ�����炸�c���̕����a���ŏ��ɂ��������邱�Ƃ��ł���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����j
���f�B�X�J�b�V�������R�����g��
�Eregression effect�́Aregression to the mean�i���ςւ̉�A�j�ƌĂ�邱�Ƃ̂ق��������悤�ȋC������B
�E�}8.1������ǂݎ���ʂ�A���ϐg���������e�̐g�����Ⴂ�ꍇ�A�\�������q���̐g���́A���e�̐g�����̂��������Ȃ�i���ϒl�ɋ߂Â��j�B����A���ϐg���������e�̐g���������ꍇ�A�\�������q���̐g���́A���e�̐g�����̂����Ⴍ�Ȃ�i���ϒl�ɋ߂Â��j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�X�{�j
�y�[�W�g�b�v�ɖ߂�
2007/07/13
Chapter 8�F8.10 �` ( pp.161 �` )�@�@
8.10 �����U���Ɛ���̕W���덷 ( Homoscedasticity and the standard error of estimate )
pp.161
�������U�����w�̒l���ꂼ��ɑ���x�̒l�̕��U���������Ȃ��ԁB
�����R���铙���U���Ƃ́A��ϐ��f�[�^�̕�W�c�̓����ł���A�T���v�������������ꍇ�ɂ͂w��2�̒l�ɑ���x�̕��U���܂������������Ȃ�ƍl����ׂ��ł͂Ȃ��B
���}8.4�FSAT�̐��т���GPA��\��
���}8.4�̔��}�����A�����F��(column)�̕��ς����Ԃƕ`�������͑傫����������O��邱�Ƃ͂Ȃ��i�W�����`�ł��邱�Ƃ�������j�܂��A���̑傫���͂قړ����ł���A�����U���������Ă���B
���w����x�𐳊m�ɗ\������1�̕��@�́A�c���̕��U�ł���B
�������덷�̕��U�́A 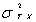 �ƕ\����A�����w�̒l�����T���v���̂x�̒l�̕��U�������B
�ƕ\����A�����w�̒l�����T���v���̂x�̒l�̕��U�������B
����8.8�@���@�p�����[�^�@�^��8.10�@���@���v�I�B�����덷���U�̕��������W�������덷
���}8.5�F�W�������덷��p���ė\���l 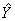 �̎��͂ɋ�Ԑݒ�i���̋�ԓ��Ɏ����l�����݁j�B
�̎��͂ɋ�Ԑݒ�i���̋�ԓ��Ɏ����l�����݁j�B
���\�������傫�ȃT���v���ɂ��ēK�p�����ꍇ�A���K�Ȑ��̂��Ƃŋ�Ԑ��肷����@���Ƃ�B
8.11 Regression and pretest-posttest gains pp.164
���o���L���Ȍ����҂ł����Ă��\�����ʂ̉e���𐳂������߂��邱�Ƃ͍���B
��pre-/post-test��2����s�Ȃ����ꍇ�Apost-test(2���)�̓��_�́A���ϒl�ɋ߂Â��X��������Bpre-/post-test���s�Ȃ��āA���т��L�тĂ���ƁA���u�Ɍ��ʂ��������ƈ�ʂɉ��߂��邪�A���ς�艺�̌Q��Ώۂɍs�Ȃ����ꍇ�ɂ́Apost-test(2���)�ł͕��ϒl�ɋ߂Â��i��A���ہj���߂ɏ����オ��B���̒��x�̏㏸�ł���Ή�A���ʂł��邩��A���u�Ɍ��ʂ��������ƍl����ׂ��ł͂Ȃ��B��F�}8.6
��pre-/post-test���ꂼ��̕ꕽ�ρ�100�A���U���������i�܂�A�u���u�Ɍ��ʂȂ��v�j�B
���W�������덷��p����Γ���pre-test���_�����l��post-test��SD��������B
��F1��ڂ̃e�X�g��70�̐l�����@�ˁ@2��ڂł�82�ƂȂ�iSD��12�j
�����K�Ȑ�����A70�̐l�����̂���84%����A���A���̂��߂�post-test�ł͓��_���L�т�B
����A���ۂ́A���u�E���K���ʂ��Ȃ��Ă��N����A�������L���Ǝv���錋�ʂł�����͒P�ɉ�A���ہA��A���ʂɂ����̂ł��邱�Ƃ�����B
���u�Ή��L��E�J�Ԃ��L��v�̕��͂ɂ����Ă��ʏ��A���ʂ̉e������B
���ꕽ�ς���O��Ă���T���v����I�сA1��ڂ�2��ڂ̓��_���r���Ă��錤������ёΉ��̂���f�U�C���̌����ɂ͒��ӂ��K�v�ł���B
8.12 �������� ( Part correlation, semi-partial correlation )
�����_�̐L�т�ω��𑪂邽�߂ɂ́Apretest�iX3�j����posttest�i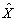 2�j�̓��_��\�����A�L�т𑪂���̂Ƃ��ĕ�SD�iX2�|
2�j�̓��_��\�����A�L�т𑪂���̂Ƃ��ĕ�SD�iX2�| 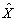 2�j��p����Ƃ悢�B
2�j��p����Ƃ悢�B
�����̕��͎c���ł���Aresidual gain�ƌĂ�Ae2.3�ƕ\���i�}8.7�Q�Ɓj�B
��e2.3��X3�̑��ւ͏��0�B�w�K���x�̑���ɂ����āAe2.3�ɂ́A�u�w�K�̒��x�͏��߂̓��_�Ƃ͑��֊W�ɂȂ��v�Ƃ������������B
��X1�iIQ�j�Ǝc��e2.3�Ƃ̑��ւ͕������ւł���Apretest X3����\���ł���posttest 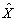 2�̕�������菜�������X1�iIQ�j��posttest X2�Ƃ̑��ւł���B
2�̕�������菜�������X1�iIQ�j��posttest X2�Ƃ̑��ւł���B
���������ւ��Z�o����K�v�́A���ڂ͂Ȃ�����8.11�ɂ�蓾����B
8.13 �Α��� ( Partial correlation �j
��X1�����X2�Ɓu�Œ肵���vX3�Ƃ̑��ւ��Α��ցA�܂�c��e1.3��e2.3�̑��ւł���B
���������ւ̏ꍇ�Ɠ��l�ɁA�Α��ւ邽�߂̎c���Z�o�͕s�v�i�Α��W���͒���r12�Ar13�Ar23���玮8.12��p���ĎZ�o�\�j�B
���Α��ւ̉��߂ɂ͒��ӂ��K�v�i��pp.168-169�j�F�ϐ��̊W�����`�ł������U�������Ȃ�A�Α��W���́u���ɂ����vX3�i�N��j��X1( reading ability )�����X2( visual perceptual ability )�Ƃ̑��W���ɓ������B
����(�\7.11)�F�R���X�e���[���l(X1)�ƐS������(X2)�̑��ւ�r��.18�ł͂��������A�ǂ���̕ϐ����N��(X3)�Ƒ��ւ�����B�����N��̐l�ɂ��ăR���X�e���[���l(X1)�ƐS������(X2)�̑��ւ�����i�N��̗v������菜���j�ƁA���ۂ̑��ւ�r��.08�ƂȂ�B
8.14 �̕Α��� ( Second-order partial correlation )
��1�̕ϐ��ɂ��e������菜�����ꍇ�̕Α��W���@�ˁ@�ꎟ�̕Α��W��
�@��2�̕ϐ��ɂ��e������菜�����ꍇ�̕Α��W���@�ˁ@�̕Α��W��
���̕Α��ցF2�̕ϐ�X3,X4��\���q�Ƃ����d��A����\�����ꂽ���X1�̎c����X2�̎c���Ԃ̑���
�@�˗�F�R���X�e���[���l(X1)�ƐS������̑���(X2)�@�ˁ@�N��(X3)�Ɛg��(X4)���Œ肵��
8.15 �d��A�Əd���� ( Multiple regression and multiple correlation )
���d��A�Fm�i�Q�ȏ�j�̓Ɨ��ϐ�����x��\������ꍇ�ɍł���ʓI�ɗp�����铝�v��@�i��8.14�j�B
�i��j��w��GPA��\�������Z�̃N���X�����ʂ�SAT��������ACT�̐���
���d��A�̖ړI�F�ő�̐��x�œƗ��ϐ�(m��)���������ĕϐ��x��\�����邱��
���P(��ϗ�)��A�F1�̓Ɨ��ϐ���p����B�ŏ����@�ɂ��b��c�̒l�͎c�������a���\�Ȍ��菬�����Ȃ�悤�ɑI���B
��b��c�͗\���l�Ɗϑ��l�Ԃ̑��ւ��ő�ɂȂ�悤��m�̗\���q���d�݂Â�����B
���\���l�Ɗϑ��l�Ԃ�Pearson�ϗ����ւ́Am�̓Ɨ��ϐ��̏d�ݕt�����ǂ���̐��x�ŏ[���ϐ���\�����A���֊W�������𑪂�B�˂���Pearson' r�͏d���ւƌĂ��B
����8.14�ɂ������A�W���ƐؕЂ͗\���l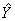 ����邾���łȂ��AY ��
����邾���łȂ��AY �� 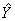 �Ԃ̍ő�̑��ւ����B
�Ԃ̍ő�̑��ւ����B
8.16 The standardized regression equation
�����ׂĂ̕ϐ����W��z-score�ŕ\�����ꍇ�Araw-score��A���i��8.14�j�͒P���������B
���W������A���ł́A�S�Ă̕ϐ��͕��ρ�0�A�W������1�̕W�����_�ɐ��`�ϊ������B
����8.16�̉�A�W����"beta weights"��W������A�W���A���邢�͕W�����Ή�A�W���ƌĂ�邱�Ƃ�����B
���ϐ��̑S�Ă̑g�ݍ��킹�ɂ����鑊�ւ���A����ɂ͕K�v�B
��raw-score��A���͗\������ɂ͂��s�����悢���Araw-score��A�W���̍���͓Ɨ��ϐ���SD�ɑ傫�����E�����̂Ŕ�r�ł��Ȃ��B�������Abeta �W���ɂ͂��̖��_�͂Ȃ��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(�����j
���f�B�X�J�b�V�������R�����g���@
�E 8.11�Ɋւ��āA�u���̒��x�̏㏸�ł���Ή�A���ʂł��邩��v�Ƃ��邪�A��̓I�ɂǂ̒��x�̏㏸�����s���ł������B
�E �������ւƕΑ��ւ��������A�Ⴂ���N���A�[�ɂ���̂���������B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(�C�j
�y�[�W�g�b�v�ɖ߂�
2007/07/26
8.17 The raw-score regression equation
���@RR (reading readiness) test��55�_�ŁAIQ��120�̐��k�̗\������镽�ς�reading grade�͂������낤���B�����̓_����W�������A8.16�ł̎��ɑ������ƌv�Z�ł���B�������Araw score�ł̉�A�� (��8.14) ���g�p����ƁA���̂悤�ȕW�����͕K�v�Ȃ��Ȃ�B
���@��8.18A�ł́Araw score�ł̉�A�W���ƃ��̏d�ݕt���i�� weights�j�́A�W�����ł���sy��sm����������Γ����ɂȂ�B
���@�W�������ꂽ��A���Ɣ�r����ƁAraw score�ł̉�A���̂ق����֗��ł���B�������A�S�Ă̕ϐ����W��������Ă���ꍇ�ɂ́A�Ɨ��ϐ��ւ̊�^��]������ɂ́A�� weights�͂��֗��ł���B
8.18 Multiple Correlation
���@�\����2�ȏ�̓Ɨ��ϐ�����s���Ă���Ƃ���Y��?�̑��ւ�multiple correlation�ƌ����A��8.19����Z�o�ł���B2�̓Ɨ��ϐ��Ԃɑ��ւ������Ƃ��ɂ́Amultiple correlation�͂��傫���Ȃ�B����2�̓Ɨ��ϐ��Ԃ̑��ւ�1�ł���Ƃ��ɂ́A�����̓Ɨ��ϐ���p���Ă��A�\���͂��ǂ��Ȃ�Ȃ��i�}8.8�Q�Ɓj�B�]���āA�d��A���͂��s���Ƃ��ɂ́A�Ɨ��ϐ��Ə]���ϐ����������ւł���A���Ɨ��ϐ����m�̑��ւ��Ⴂ���Ƃ��]�܂��B
���@�߂����ɖ������Ƃł͂��邪�A�]���ϐ��Ƒ��ւ������Ɨ��ϐ���multiple correlation�����߂邱�Ƃ�����B����́A���̓Ɨ��ϐ��ł̖��W�ȕϐ���}�����邱�Ƃɂ���ċN����B���̂悤�ȏꍇ�A���̕ϐ���suppressor variable�ƌĂ��B
8.19 Multiple Regression Equation with Three or More Independent Variables
���@3�ȏ�̓Ɨ��ϐ��������A�W���̌v�Z�́A���_�I�ɂ͕��G�ł͂Ȃ����A��v�Z�ōs���Ǝ��Ԃ��������Ă��肷��B�������A���ۂɂ̓R���s���[�^�[�v���O�����ōs���̂Ŗ��Ȃ��B
8.20 Stepwise Multiple Regression
���@8.18�ł́Aadditional predictor���Ǝ��Ɋ�^����̂ł���Ό��ʓI�ł��邱�ƂɐG�ꂽ�B�����̏ꍇ�Astepwise ��A���͂��s���B���̕��@�ł́A�ł���^����Ɨ��ϐ����ŏ��̒i�K�Ƃ��đI��A���̓Ɨ��ϐ������ɂ���A�W����standard error of estimate�Ȃǂ��v�Z�����B���̒i�K�Ƃ��āA�ŏ��ɓ������ꂽ�Ɨ��ϐ��ɂ��\�����Ȃ������ŁA�ł���^����Ɨ��ϐ������������B
8.21 Illustration of Stepwise Multiple Regression
���@�u���k�̔N��A���ʁA�Љ�o�ϓI�K���Areading readiness�AIQ����A���w�N���̓lj��p�t�H�[�}���X�͂ǂ̒��x���m�ɗ\���ł��邩�v�Ƃ����₢�ɑ��āA�\8.3�͑��ցA���ρASD�������Ă���B
���@�\8.4��stepwise multiple regression�̗v��ł���B�\8.3��SES�̕������ʂ��Y�i�\���ϐ��j�Ƃ̑��ւ��������A�\8.4��Step 3�ł͐��ʂ��I��Ă���B����́ASES�̕ϐ��������ʂ̕����A���2�̓Ɨ��ϐ���⊮���Ă��邽�߂ł���B�܂�A�̕Α��ւł͐��ʂ̕������W���������B
8.22 Dichotomous and Categorical Variables as Predictors
���@���ʂ̂悤�ȃC�`�[���f�[�^�ł��A���l�̃R�[�f�B���O���Ȃ���Ă���ΓƗ��ϐ��Ƃ��ėp���邱�Ƃ��ł���B�������A���̃R�[�h�͓_�o�W�������߂����O�ɍs��Ȃ���Ȃ�Ȃ��B
���@3�ȏ�̃J�e�S���[�����閼�`�ϐ��́A�Ɨ��ϐ��Ƃ��ėp���邽�߂ɂ�J-1��dichotomies (dummy��indicator variables�ƌĂ�邱�Ƃ�����)�ɕ����Ȃ���Ȃ���Ȃ�Ȃ��B�Ⴆ�A3�̖����O���[�v���������Ƃ�����A2�̓Ɨ��ϐ����K�v�ł���B�܂�A�u�����O���[�vA�ɑ����Ă��܂����H�v�Ɓu�����O���[�vB�ɑ����Ă��܂����H�v�Ƃ������̂ł���B����痼����No�ƃR�[�f�B���O����Ă���A�����O���[�vC�ɑ����Ă���Ƃ������ƂɂȂ�B
8.23 The Standard Error of Estimate in Multiple Regression
���@�\8.4�ŁACA��p���邱�Ƃł̗\�����̏㏸�͂قƂ�nj���ꂸ�A�܂��W���덷�͑����Ă���B�ł��ǂ�3��4�̕ϐ����������ꂽ��́A��A�W���͂قƂ�Ǖω����Ȃ��A�Ƃ����悤�Ȃ��Ƃ͗ǂ��N���邱�Ƃł���B
8.24 The Multiple Correlation as an Inferential Statistic: Correlation for Bias�i�悭�킩��܂���ł����j
���@��A�W���́AY��?�̑��ւ��ł������Ȃ�悤�Ɍ��肳��邪�A���̂悤�ȏ����̍ۂ�fitting error���\���B���̌덷����菜�����@�Ƃ��āA��8.21���ł��L���g�p����Ă���iSPSS�ł̏C�������̒l�炵���j�B
���@�����ŎZ�o���ꂽR�͕\8.4�ŎZ�o���ꂽ���̂������Ⴂ�Bn�̒l���������Ȃ�قǁA������m�̒l���傫���Ȃ�قǑ傫���C������Ă��܂����߁A��8.22��p����A��8.21�͕K�v�Ȃ��B
���@������8.21��p����̂ł���A�S�Ă̓Ɨ��ϐ��𓊓����Ă���s���ׂ��ł���B
8.25 Assumptions
���@��A�ɂ����ẮA�ȉ��̑O�K�v�ł���B
1. Y scores�͓Ɨ��ŁA��A�����̑S�Ă̓_�Ő��K���z���Ă���A�܂��c�������K���z���Ă��邱�ƁB
2. ?��X����ɂ���Y��Y����ɂ���ꍇ�AY��?�̊Ԃɂ͐��`�ȊW������B
3. �c���̕��U�͑S�Ă�?�ɑ��ē����ł���B�����homoscedasticity�ƌĂԁB
8.26 Curvilinear Regression and Correlation
���@���̔F�m�I�E�S���^���I�ȕϐ��͐��`�ł���B�������A�������`�ł͂Ȃ��Ƃ��ɂ͕ϊ�����ׂ��ł���i8.28�ň����j�B�������̕ϊ������s�������ꍇ�ɂ́A��蕡�G�ȉ�A����p���邪�A���̃R���s���[�^�[�v���O�����ɂ́A���̂悤�ȉ�A���������v���O�������܂܂�Ă���B
8.27 Measuring Nonlinear Relationships Between Two Variables: ��
���@�s�A�\����r�͐��`�W�����`�ʂł��Ȃ����A�������`�łȂ��ꍇ�ɂ͂ǂ�����悢���낤���BFigure 8.9�ł́A40�܂ł͏㏸���A����Ȍ�͉��~���Ă��邱�Ƃ�������B��8.23�ł́A2�ϐ��̊W�i���`�E����`�j���łŕ\�����Ƃ��o����i��2�͑��֔�ƌĂ��j�Br�Ƃ͈قȂ�A�ł͏�ɐ��̒l�ł���B��Y.X��Y��X���� "best-fitting" line�i�����E�Ȑ��j�ɂ���ė\���������x�ł���A��Y.X�ƃ�X.Y�͒ʏ�قȂ�B
8.28 Transforming Nonlinear Relationships Into Linear Relationships
���@����`�ȊW�́A���`�ɋ߂��W�ɕϊ��\�ł���iLog�A���A�O��Ȃǁj�B
8.29 Dichotomous Dependent Variables: Logistic Regression
���@�d��A���͂͐����A�����Ă���ꍇ�̃p�t�H�[�}���X��\��������̂ł��邽�߁A�ϐ����C�`�[���▼�`�ϐ��ł���ꍇ�ɂ͂��̑O��������Ȃ��BLogistic regression�̑O��͏d��A���͂̑O��Ƒ�ϗގ����Ă��邪�Alogistic regression�͏]���ϐ����Ɨ��ϐ��̐��`�W�ł��邱�Ƃ�O��Ƃ��Ȃ��B
���@Logistic regression�͏d��A�����O���Ȃ����A�T�O�͏d��A���͂��ł���B
8.30 Categorical Dependent Variables With More Than Two Categories: Discriminant Analysis
���@�]���ϐ���2�ȏ�̖��`�ϐ��ł��邱�Ƃ́A���܂茩�����Ȃ����A���ʕ��͂����̂悤�ȏꍇ�ɍł��L���p������BDiscriminant score�Ɋ�Â��āA����J�e�S���[�ɂȂ�m�������ꂼ��v�Z�����_�ŁA�d��A���͂Ƃ͈قȂ�B
8.31 Chapter Summary
���@���_��1-r��SD unit�ŕ��ςɉ�A����B?��Y�̍��͎c����errors of estimate�ƌĂ�A�W�������ꂽ���̂�standard error of estimate�ƌĂ��B
���@��A������least squares criterion�ɂ���Č��߂���B�o�C�A�X�i�덷�H�j�͓Ɨ��ϐ��������Ȃ�A�܂��T���v���T�C�Y���������Ȃ�قǑ傫���Ȃ�B
���@Stepwise multiple regression�ł́A�]���ϐ��ƍł����W���������������̂��ŏ��ɓ��������B
���@2�̕ϐ��Ԃ̊W�����`�ł͂Ȃ������ꍇ�ɂ́A�ł�p����Ɨǂ��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(�X�{�j
���f�B�X�J�b�V�������R�����g
r2�͐������ł���A���W���Ƃ͈قȂ�B
�d��A���͂��s�Ȃ��Ƃ��ɂ́A�Ɨ��ϐ��Ə]���ϐ����������ւł���A���Ɨ��ϐ����m�̑��ւ��Ⴂ���Ƃ��]�܂�邪�A����͎��̂悤�ȗ��R�ɂ��F�Ɨ��ϐ����m��r = .90�ȏ�Ȃ�݂��ɑj�Q����\�������邽�߂ɁA�d��A���͂���͊O���B
�̕Α��ց@���@partial correlation
Logistic Regression��p����̂́A�]���ϐ���0.1�̎��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(����)
�y�[�W�g�b�v�ɖ߂�
2007/08/24
Chapter 9 (pp.199-221)
9.1 Introduction
���m���l���琄��������@�����W���Ă��邪�A�u�����v�̐��ۂ�"extremely unlikely"����"almost certain"�܂ŕ��L���B
���m�����_�͕��G�ł��邪�A�����̌����Ԑ���̓��v�f�[�^�����߂���ɂ͊m���𗝉������钼�����K�v�ƂȂ�B
9.2 Probability as a mathematical system
���W�{��� ( sample space )�F�������邢�͊ώ@�̌��ʋN����\����_�i�W�{�_�j�ŕ\�����Ƃ��̑S�Ă̓_�̏W���ievent space�Ƃ������j�B
������ ( event )�F�ώ@�����錋�ʁB�ʏ�A���t�@�x�b�g�̑啶���ŋL���B
����F�ڂ̒��ɔ����{�[�����U�ƍ����{�[����3��
�˕W�{��ԁ�9�_�B1�{�[�������o���Ɓu�����{�[���v�ł��錋�ʁ�����
������A���N����m����P(A)�ŕ\���i�����Ȃ鎖�ۂ��l��0����P�j�B
������A�Ǝ��ۂa���݂��ɔr���i���ʂ̓_���܂�ł��Ȃ��j�ł���Ƃ��A����A���邢�͎���B���N����m���́A�e���ۂ��N����m���̘a [ P(A or B) = P(A) + P(B) ]
�ˁ@�\���FA��B�i�J�b�v�A���j�I���A���сj
9.3 First addition rule of probabilities�i���@�藝�F�a���ہA�ώ��ہj
���݂��ɔr���ł��鎖��A, B�̏ꍇ�A����A���邢�͎���B���N����m����P(A��B)
��P(A��B) = P(A) + P(B)
���݂��ɔr���łȂ�����A, B�̏ꍇ���
����F3��A���ŃR�C���𓊂���or 3�̃R�C������x�ɓ������ꍇ�A�W�ʂ�̌��ʂ��������\�B
����A = Heads on flips 1 and 2
����B = Heads on flips 2 and 3
����A�Ǝ���B���i�����Ɂj�N����m���́H
9.4 Second addition rule of probabilities
���x���}9.1(p.203)�@���Q�̎��ۂ݂͌��ɔr���łȂ��i���ʂ̕W�{�_������j�B
���x���}9.2(p.204)�@���Q�̎��ۂ��݂��ɔr���ł���B
��P(A��B)�����߂�ꍇ�̎�9.5(p.203)
�ˎ���A, B���݂��ɔr���łȂ��ꍇ�A�e���ۂ̋��ʓ_P(A��B)��2��d�����ĉ����Ă��邱�ƂɂȂ�Bintersection�i��_�j�̏d��������邽�߂ɁA�����B
���吔�̖@���F�m�����_�̓K�p�ɏd�v
9.5 Multiplication rule of probabilities�i��@�藝�j
����9.6(p.205)
��P(A)�ł��鎖��A���A�Ɨ�����r��r��N����m��
�����ۂ̓Ɨ����́A���v�w�Ɗm���ɂ����ďd�v�ȊT�O�ł���B
9.6 Conditional probability�i�����t���m���j
����9.7(p.206)
��P(B?A) = ����A���N�������A�Ƃ��������̂��ƂŎ���B���N����m���B
���FP(A?B) = ����B���N�������Ƃ��������̂��ƂŎ���A���N����m���ł���A
P(B?A) �� P(A?B)�ł���B
���x���}9.1����
����Fp.207, 2nd paragraph
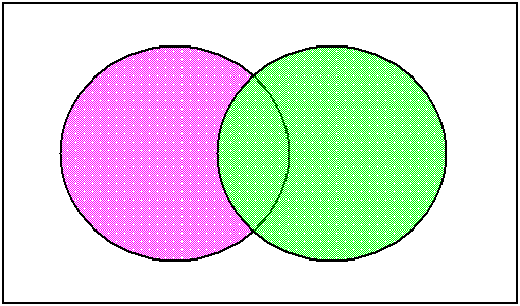
9.7 Bayes's theorem�i�x�C�Y�̒藝�j
����9.7�̓x�C�Y�̒藝�i���܂��܂ȏ����t�m���Ԃ̊W�������j�̍ł��P����version�B
�����O�m�������m�ł���A�x�C�Y�̒藝�ɂ�萳�m�Ȍ��ʁi���]�̊m���j�������邪�A���̎��O�m���邱�Ƃ����ۂ͍���ł���A���v�w�҂̊Ԃł͑傢�ɕ��c���������Ă���B
9.8 Permutations�i����j
���l���Ώۂ̎����ɂ��Ă̔z���˗�FTable 9.2(p.208)
��N�̑Ώە�����ׂ��ꍇ�̏���͉��ʂ肠�邩�H
�� N! �ƕ\���A"N�̊K��"�A"N factorial"�ƓǂށB
��N!��1����N�܂ł̐����̐ςŁAN�̑Ώە��̏��ɓ�����(0!�͐��w�I��1)�B
��N!�̒l�́AN�̐���������ƒ������傫���Ȃ�B
9.9 Combinations�i�g�ݍ��킹�j
��N�̂��̂���r�����o���ꍇ�ŁA���̍ۂɏ���͍l������Ȃ��B
�� r = N�̏ꍇ�F�S�Ă̑Ώە������o����A�g�ݍ��킹��1�̂݁i����N!�͂��邪�j�B
r = 1�̏ꍇ�FN�̒�����1���������o���̂ŁAN�̑g�ݍ��킹������B
��N���珇��͍l��������r�����o���g�ݍ��킹�̐��́AN����r�����o������1�̑g�ݍ��킹���̏��Ŋ��������ɓ������B
����9.10�̍��ӂ́uN����r�����o���g�ݍ��킹�̐��v�Ɠǂ݁A�E�ӂ̕��q�Ɏ�9.11��������Ǝ�9.12�ɂȂ�B
9.10 Binomial probabilities�i�m���j
����9.13�FN��̓Ɨ����s�̒���A���N����m����p�Ƃ��AB�iA�ł͂Ȃ����Ɓj���N����m����q = 1-p�Ƃ���ƁAN��̎��s���Ɂu�����iA�j�v��r��N����m�������߂�B
����F(p.211, 3rd paragraph)
Table9.1�̐ԂƗ�2�̃T�C�R���𓊂���7�ɂȂ�m���́Ap = 6/36 = 1/6�ƂȂ�Bq = 1-p = 5/6�ƂȂ�B����āA�S����5���āA4��7�ƂȂ�A1��7�ȊO�̐��ɂȂ�m���́H
���W�J�@( binomial expansion )�F���̎��s�Ŏ���A���N����m����p�Ƃ���ꍇ�AN��̃x���k�[�C�Ɨ����s�Ŏ���A���N����̊m�������߂�����@�B
�ˁ@��9.15
9.11 The binomial and sign test
����������FN�g�̊ϑ����ʂ�������z��"non-parametric"�@�̈�B
�����鎖�ۂ��N����m�����A��9.15���狁�߂����l�ŒႢ�Ƙ_�����キ�Ȃ邪�Acase���d�˂Ă��������Ȃ��Ă����B
9.12 Intuition and probability
���u�m���v�͓q�����Ƃ̊֘A�Ői�����A�m�����_�𗘗p����l�X�́A�����ł͓��ӂ����˂錋�ʂݏo�����̗��_�̎d�g�݂ƕ��G���ɋ�����Ȃ����B
���m���͏W�c���̐����傫���Ȃ�ɏ]�������Ȃ���̂ł���B
�����̎��ۂ��N����m�����Ɨ��ł���Ȃ�A���̐悻�̎��ۂ��N����m���͉ߋ��̂����Ȃ�p�^�[���̌��ʂɂ��e������Ȃ��i�����t�m���������ɂ��F��9.7�j�B
9.13 Probability as an area�i�ʐρj
���A���m���ϐ����琄�肳���l����ŕ`���ƁA����2�̒l�Ƃ��̐��ň͂܂�镔���i�ʐρj�́A���̕ϐ���2�ϐ��Ԃ̂���l�𐄒肷��m���Ɠ������Ȃ�B
���}9.4�F0����2�̊ԂŁA�������m���łǂ�Ȓl����肤��m���ϐ���X�Ƃ���B�S�Ă̒l�ɑ���P(X) = .5�ł���ꍇ�̊m�����x����\���Ă���B
9.14 Combining probabilities
�������̊m���i���茋�ʁj�������@�ˁ@Stouffer-method (Rosenthal, 1978)
���X�̌��茋�ʂ�p�l��Table A(p.616)�̑Ή�����z�l�ɕϊ����A���������v����B���ɁA����̌��̕������Ŋ���B����z�l�ɑΉ�����p�l��Table A�ɂ��ϊ�����B�������ꂽp�l���A�L�ӂ��ۂ��̌��_��B
����L��@�ł́Ap�l�͂��ꂼ��Ɨ����Ă��Ȃ���Ȃ�Ȃ��B���d������s�Ȃ��P��̌������ł͎g�p���Ă͂����Ȃ��B
9.15 Expectations and moments�i�ϗ��j
�����[�����g�i�ϗ��j�F����W�c���ǂ̂悤�ȕ��z���������ɂ��āA���Ғl�̊ϓ_���炻�̕��z�̓����i���z�̕��ϒl��o���c�L�A�Ђ��݂���x�j�𐔒l���B
����9.16�FX�����U�m���ϐ��ł���ꍇ��X�̊��Ғl�AE(X)��\���B
��E(X) = �ʂƂ��\���B
��X���A���ϐ��̏ꍇ�A�㐔���ɂ���Ċm�����z���������Ƃ��ł���BX���A���ϐ��ł���ꍇ�A�P���X�̒l�Ɋm����t�^���邱�Ƃ͂ł��Ȃ����AX�͂����Ԃɑ��݂���Əq�ׂ邱�Ƃ͂ł���B
�˂��̂��Ƃ���A��9.16�ɂ�蓾����E(X)�̒�`�͘A���m���ϐ��ɂ͓K�p�ł��Ȃ��B
���}9.5�FX��2�`3�̒l���Ƃ�m���́A�Ȑ���2�̒l�ň͂܂ꂽ�ʐςƓ��������Ƃ������B
���A���m���ϐ��̊��Ғl�́A�ϕ��@�ɂ���ċ��߂���B�\�L�@�͗��U�m���ϐ��̏ꍇ�Ɠ�����E(X)���邢�̓ʁB
�Q�l�F
�{�� ���j (1999). ��{���v�w�i��3�Łj�L��t
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����j
�f�B�X�J�b�V�������R�����g
�E���[�c�B�[�iyahtzee�j�Ƃ����Q�[���̘b���o�āA�m�����q�����Ƃ���i�������̂��悭�킩�����B
�E9.14�ŁA�����̌��ʂ���������ƗL�ӂɂȂ�₷���Ȃ����̂ŁA����͗ǂ��̂��ǂ����킩��Ȃ��B���^���͂ɋ߂����@���낤���A�����̌������ʂŗL�ӂł͂Ȃ����L�ӂɋ߂��Ȃ��Ă����̂Ȃ�A��������Ƃ���͈Ӗ������鍷�ɂȂ�A�Ƃ������ƂȂ̂��낤���H
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�X�{�j
�y�[�W�g�b�v�ɖ߂�
2007/09/14
Chapter 10, pp.223-239
10.1 Introduction
���{���v�I��@�̑��̖ړI�́A�T���v������̃f�[�^��p���ĕ�W�c�ɂ��Ă̈�ʉ����s�����Ƃł���B�����ł́A�{�͈ȍ~�ō��{�I�ɕK�v�ƂȂ�A�C�f�B�A�������Ă����B
10.2 Populations and samples: parameters and statistics
�����v�I���_(statistical inference)��p���邱�Ƃ̖{���́A��r�I�������W�{�W�c(sample)����傫����W�c(population)�Ɋւ���m���邱�Ƃł���B�T���v�����K�ȕ��@�ŕ�W�c���璊�o����邱�Ƃɂ��A��W�c�̓��������炩�ɂȂ�B
����W�c�ɑ��Čv�Z�����l���p�����[�^(parameter)�A�T���v���ɑ��Ă͓��v(statistics)�ƌĂ��B
�����ϓ_�̓T���v���̏ꍇX�o�[�A��W�c�̏ꍇ�̓ʁA���U�Ɋւ��Ă̓T���v����s^2�A��W�c����^2�ƕ\�L�����B�܂��A���vr�̓p�����[�^���̐���(estimate)�ł���B���̐��肪�p�����[�^�ɂ��Ă̏�����邱�ƂɂȂ�B
10.3 Infinite versus finite population
�������I����(�w�Z����l����)�͗L���ł�����̂́A��W�c�̃T�C�Y�͖����ł���Ƒ�����ꂪ���ł���B
���������A���̂悤�ȋ�ʂ�S�z����K�v�͂Ȃ��B�T���v���Ƃ��Ē��o���ꂽ�v�f�̊�����5�����傫���Ȃ�Ȃ�����A�L��������̗����ɑ���e�N�j�b�N�͓������ʂ������炷�Ƃ���Ă��邩��ł���B
���܂�A�قƂ�ǂ̉��p���v�I��@�͖����̕�W�c���T���v���Ƃ��Ē��o�����Ƃ�������Ɋ�Â����̂ł���B
10.4 Randomness and random sampling
�����v�I���_�̑Ó����ɂ����ẮA�T���v�����ǂ̒��x��W�c���\���Ă���̂��Ƃ������Ƃ��ł��d�v�Ȃ��ƂƂȂ�B
���T���v�����ǂ�Ȃɑ傫���Ă��A���ꂪ��\��(representativeness)�̌��@�������߂��邱�Ƃ͂Ȃ��̂ł���B
10.5 Accidental or convenience samples
�����̒��o�@�͂悭�g�����@�ł��邪(�Ⴆ�ΊX�p��f�B�A�ɂ���ĕ����@)�A�K�ł���Ƃ͌����Ȃ�(��\���Ɍ�����)�B
10.6 Random samples
����\���Ɋւ��Ă͂����ł����ɂȂ邪�A�T���v���������_���ɒ��o�����A���̃T���v���͕�W�c���\����X���ɂ���Ƃ������ƂɂȂ�B�܂�A�����_�����o�́A��������(��W�c�ƃT���v���Ԃ�)�덷�͈͓̔��ő�\����ۏ�����̂ł���A�p�����[�^������̉\���������ė����������x�̐ݒ�����e����̂ł���B
�����̃G���[�𐄒肷��\�͂������_���T���v�����O�ɂ�����d�v�ȓ����ł���B�܂�A���v�I���_�̃v���Z�X�̓T���v������p�����[�^�̐�����s�����ƂƁA���̒��ŃT���v�����O�G���[�̑傫�������肷�邱�Ƃ��܂܂��B���̃G���[��10���ȉ��ł���ׂ��ƌ����Ă���B
���܂��A�����_���Ȓ��o�̓V�X�e�}�e�B�b�N�ȃo�C�A�X������邱�Ƃɂ��Ȃ�B
10.7 Independence
�������_���T���v�����O�ł́A�T���v���Ƃ��Ē��o�����l�ɂ́A���o�̉\���Ɍl�Ԃō����Ȃ��A���l����̉e�����Ȃ����̒��o�̓Ɨ������ۏႳ��Ă��Ȃ��Ă͂Ȃ�Ȃ��B
������Ɋւ��錤������ɂ����āA���ɑΏۂƂ���N���X��w�Z��I������ۂɂ��̂悤�Ȗ��Ɋׂ�₷�����Ƃ͗��ӂ��Ȃ��Ă͂Ȃ�Ȃ��B
���������A�����I�Ɋ����ȃ����_���T���v�����O��B�����邱�Ƃ͕s�\�ł���̂������ł���B
10.8 Systematic sampling
���Ⴆ�����_���ɑI�������ԍ�(�����ł�13)����A43�A73, 103, �c2983�Ƃ����悤��30�Ԓu���̔ԍ���I�����Ă����Ƃ��T���v���̒��o�@���V�X�e�}�e�B�b�N�T���v�����O(systematic sampling)�ƌĂԁB
�����_�Ƃ��Ă͎��{���e�Ղł��邱�ƁA�����_���T���v�����O�����킸���ɐ��m���������A�G���[�����Ȃ����ƂȂǂ��������邪�A�����I�Ȏ���ł́A���肪�ǂ̒��x���m�Ȃ̂��Ƃ������Ƃf�����i�Ɍ�����Ƃ������Ƃ��A���_�Ƃ��ċ�������B
���������A�K�ɍs����A���X�̍���������̂́A���҂̎�@�̌��ʂ���ʉ����邱�Ƃ͉\�ƂȂ�B
10.9 Point and interval estimate
��Point estimates�Ƃ̓p�����[�^�𐄒肷��Ƃ��ɗp������P��̒l�ł���BInterval estimates�Ƃ͐���̓x�����̐��m����\��point estimates�̊T�O��ɗ��Ă��Ă�����̂ł���B
��E(X�o�[)���ʂ�X�o�[���ʂ�unbiased point estimates�ł��邱�Ƃ������B
��Interval estimates�̓p�����[�^�̏㉺�����������̂ł���APoint estimates�����ł͂��̐��肪�ǂ̒��x���m�Ȃ̂��m�邱�Ƃ��ł��Ȃ��B
10.10 Sampling distribution
���Ƃ����W�c����n�l�̃T���v���𒊏o���AX�o�[���v�Z����Ƃ����v���Z�X��1000��J��Ԃ����Ƃ���ƁA�T���v���̓��v(statistic:�Ⴆ�Ε��ϒl)�̓x���̕��z(frequency distribution)��1000�ʂ蓾���邱�ƂƂȂ�B�܂�AX�o�[�̓x�����z�����ϒl�̕W�{���z(sampling distribution)�ƂȂ�B
10.11 The standard error of the mean
���W�{�̕��ϒl�ƃp�����[�^(��)����ǂ̒��x����Ă���̂��A�܂�T���v�����O�G���[�̑傫�����Z�o����ꍇ�ɂ͎�(10.1)��p����B
����X�o�[�ŕ\����镽�ς̕W���덷(the standard error of the mean)�Ƃ́A�T���v���̕���(X�o�[)�ɂ�����T���v�����O�G���[�̕W�����ł���B
�˃����_���ɒ��o���ꂽ�T���v���̕��ς����߂�Ƃ����v���Z�X���ɌJ��Ԃ������ʁA���邱�Ƃ��ł���W����(��X�o�[��3.0)�B
10.12 Relationship of ��X�o�[ to n
���T���v���̐�(��)��4�{�����ƁA��X�o�[�͔����ɂȂ�B
��E(X�o�[)���ʂ́A�T���v���̕��ς̊��Ғl�̓p�����[�^�Ɠ����ł��邱�Ƃ������B�܂�A���v�̊��Ғl�͕W�{���z�̕��ϒl�ł���A�Ƃ������Ƃ��ł���B
10.13 Confidence interval
����W�c�̕��σʂ𐄒肷�邽�߂ɂ�X�o�[���ǂ̂悤�Ɏg���悢�̂��낤���B����n=225�̏ꍇ�A��X�o�[��1.0�ƂȂ�A�W�{���z�ɂ�����68���̕��ς��ʂ���1.0����Ă���ƌ������Ƃ��ł���B�܂�A�T���v���̕��ς̎��Ӌ��68���Ƀʂ̒l�����݂��Ă���A�M�����.68��X�o�[+/-��X�o�[�ł���ƌ�����(10.2)�B
���M����ԂƂ��Ă�.95���悭�p������(10.4)�B
10.14 Confidence intervals when �� is known: an example
��100��s��IQ�e�X�g�ŁA50000�l�̂��ǂ��̕���ID��\�������B
������100�A�Ё�15�A�M����Ԃ�.95�ŕ��͂������ʁA�T���v���̕��ς�105�ł���A.95CI=105+/-2.94�ƂȂ����B�܂�A�Ђ͍Œ�102.6, �ō�107.94�̊Ԃɑ��݂��邱�Ƃ����������B
����荂�����m�������߂�Ȃ�A�܂�M����Ԃ����߂�̂ł���A�T���v���̐l���𑝂₳�Ȃ��Ă͂Ȃ�Ȃ��B
10.15 Central limit theorem: A demonstration
�����S�Ɍ��藝(Central limit theorem)�Ƃ́A����ׂɒ��o���ꂽ�T���v���̕��ς̕W�{���z���A��W�c�̌`�Ɋւ�炸���K���z�ɋ߂Â��Ƃ������_�ł���B
�����S�Ɍ��藝�̑Ó������������߂ɁA�قȂ�3�̕�W�c(���K�A�����`�A�c:��=100; ��=15)��1����25�܂ł̃T���v�����ɂ���Ăǂ̂悤�ȉe�����A�ǂ̂悤�ɕω����Ă����̂���Figure 10.3�Ɏ������B����2�̈�ʐ���������邾�낤�B
�@��W�c�ɐ��K���������Ȃ��Ă��An���㏸����ɂ�ĕW�{���z���}���ɐ��K���ɋ߂Â��B
�An�̑����ɔ����AX�o�[�̕W�{���z�̕ϓ���(variability)�͌�������B�������A���̌����͕�W�c�ɐ��K���������Ȃ��Ă���10.3�ɂ���Đ��m�ɐ��������B
���Ⴆ��Panel D�̍��̃O���t�ł́A���ϒl��10000��J��Ԃ��v�Z����Ă���B���ꂪ1000000��J��Ԃ����Ȃ�A�W�{���z�͊��S�ɐ��K���𐬂����E�Ώ̂ɂȂ�͂��ł���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i����j
�f�B�X�J�b�V�������R�����g
�E�L���̏W���ł���ꍇ�A�T���v��������W�c��5%�i��������10%�j�ȉ��Ȃ�L���E�����̋�ʂ�S�z����K�v�������Ƃ����̂́A�T���v���̊������������قǁA�w��ɉ��肷���W�c�������ɋ߂��Ȃ邩��ł��낤���B
�E10.6�̃G���[��10%�ȉ��ł���ׂ��Ƃ����̂́A����10%�ȉ��ł���ׂ��Ȃ̂��낤���B
�E10.8��systematic sampling�̕���random sampling�������m�������܂�̂́Arandom���ƕ��Ă��܂��\�������邽�߁Bsystematic
sampling�ł́A��\�������Ⴍ�Ȃ�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�X�{�j
�y�[�W�g�b�v�ɖ߂�
2007/09/28
Chapter 10 �㔼,�@pp. 239 - 253
10.16 The use of sampling distributions
���W�{���z (sampling distribution) �͕�W�c����T���v���𒊏o�����Ƃ��J��Ԃ��s�����Ƃɂ���Đ��肳��邪�A���ۂɂ͕�W�c�����x����n�̃T���v�������W���A�M����� (confidence interval, CI) �𐄒肷�邱�Ƃ��s���Ă���B��W�c�̕��σʂ� .95CI ����O���\����5���ł���Ƃ�����B
10.17 Proof that�@(��x�o�[)^2 = ��^2/n
<�v�Z���̑O��>
�����ϒl�ʁA���U��^2������W�c����W�{ (X) ���J��Ԃ����o����ꍇ�A�W�{�̕��ϒl��
(X1 + �c + Xn) / n �ƂȂ�BX�o�[�̊��ҒlE (X�o�[) �́AE [(X1 + �c + Xn) / n]
�@�����ŁA�W�{X���S�ĕ�W�c�Ɠ������ς╪�U�������Ă���Ɖ��肷��ƁA�v�Z���͎��̂悤�ɂȂ�F�@
�@E (X�o�[) = (1/n) (��+��+ �c + ��) = (1/n) (n��) = ��
������ n = 1 �̕W�{���J��Ԃ����o�����Ƃ���ƁA��W�c�̕��z�ƁA�W�{���z�͓������Ȃ�B
(��^2/n =��^2/1 =��^2)
�������_�����o���ꂽ�T���v���̕��U�ɂ��āB�e�T���v���Q�̓����_���ɏW�߂��Ă���̂ŁA���֘A�ł���A���� (correlation) �⋤���U (covariance) �̒l���[���ł���B
�������A���ꂼ��̐��l�ɒ萔 (e.g., 1/2) ���|������ƁA���̕��U�͌��X�̐��l���g�������U�����̒萔�̓�悵���l (e.g., (1/2)^2) �Ŋ|�����l�ƂȂ�B
�E�E�E�Ȃ�
��<�v�Z��10.7> ���U����^2�̕�W�c���烉���_�����o���ꂽn�̃T���v���̕��ς̕��U�́A
(��x�o�[)^2 = ��^2/n
��(��x�o�[)^2 �́Avariance error of the mean �Ƃ���B���̕������̐��̒l��standard error of the mean�Ƃ���B<�v�Z��10.8>
10.18 Properties of estimators
���\���ϐ� (estimator) �̓T���v���Ɋ�Â����v�l�ł���A��W�c�̃p�����[�^�ɉ����ăG���[�̒l���܂܂��B(�悭������Ȃ�)
���Ⴆ�A��W�c�̕��σʂ̗\���ϐ��͕W�{�̕��ϒlX�o�[�ł���Ƃ�����B�������A���ϒl�ȊO�ɂ��A�����l��ŕp�l�ȂǁA���܂��܂ȗ\���ϐ����g�p�ł���B�������AX�o�[���ł��ǂ��ƍl������B���̗��R�Ƃ���unbiasedness, consistency, efficiency������B
10.19 Unbiasedness
�����肳����W�c�ɂǂ̂悤�ȓ���������ꍇ�ɂ����Ă��A�W�{�̕��ϒlX�o�[�͕�W�c�̕��ϒl�ʂ�unbiased estimator�ł���B�܂�A��W�c�̕��ς�100�ł���Ƃ��A���o�����W�{�̕��ϒl���ق�100�ƂȂ�Ƃ�����B
�����ϒl�ƈقȂ�A�o�C�A�X�̂���l������B�Ⴆ�Ε�W�c�ɂ������̕ϐ��̑��ւ������ς𐄒肷��ꍇ�A�W�{�̑���r�͏�Ƀς����Ⴍ�Z�o����Ă��܂��B���̂悤�ȏ�����negatively biased�Ƃ����B
�t��E (�ƃn�b�g) > �ƂƂȂ邱�Ƃ���A�ƃn�b�g�́Apositively biased�Ƃ����B
���W�{�̕��U��S^2 = ��(Xi - X�o�[)^2 / (n - 1) �ł���B
�P����n�Ŋ�����@���l�����邪�A��(Xi - X�o�[)^2 / n�̓�^2�̂Ƃ���negatively biased estimator�ł��邽�ߗp�����Ȃ��B�������A100�ȏ�̃T���v��������A(n - 1) / n �̒l�� 1 �ɔ��ɋ߂��Ȃ�̂ŁA�o�C�A�X�͏������Ȃ�ƍl���Ă悢�B
�� n - 1 ���g�p����鍪���͓��ɂȂ����An - 1 �Ƃ��邱�Ƃ�unbiased estimator�ɂȂ邱�Ƃ�������Ă���킯�ł͂Ȃ��B
������AS^2����^2�̗\���ϐ��Ƃ��Ďg�p���鎖�͐��w�I�ɏؖ�����Ă���B<�v�Z��10.9�A10.10>
��10.9��10.10�̌v�Z���ɏ�����Ă���ʂƃЂ̍��́As / [4 (n - 1)] �ł���B���̌v�Z������An�����ɏ����Ȓl�łȂ�������A�o�C�A�X�͏������ƍl������B
��Table 10.2 �ɁA���ꂼ���estimator ��parameter �̐���ɍۂ��A��W�c�̕��U�ɂ���ăo�C�A�X�������邩�ǂ����������Ă���B
10.20 Consistency
���o�C�A�X�̗L���ɂ�����炸�A��ѐ��̂��錋�ʂ��Y�o�����f�[�^�ł���T���v�����������Ȃ�ɂ�Ă�value of the parameter�ւƋ߂Â��B
10.21 Relative efficiency
���o�C�A�X���ѐ�����efficiency�̕����d�v�ł���B����efficiency�Ƃ͗\���ϐ������W�c�𐄒肷��ۂ̐��x���w���B�܂��Aefficiency�Ƃ͗\���ϐ��Ɋ֘A����T���v�����O�G���[���w�����Ƃ�����B
���W�{���z�̕��U��variance error�Ƃ��Ă���B
���Ⴆ�Ε�W�c�̕��σʂ𐄒肷��ꍇ�An�̃T���v���̕���X�o�[�⒆���l��unbaiased estimator�Ƃ�����B�������A���ۂɂ�X�o�[�̕����ǂ��Ƃ���闝�R�ɂ�X�o�[�̕����A���U�����������߁A���x�������ƍl������Ƃ����_������B
�@�E�T���v���̒����l�̕��U�̎Z�o���@�@<�v�Z��10.11>�@�@�@�@��X�o�[��2/3���x�̐��x
�@�E�T���v���̒����l��standard error�̎Z�o���@�@<�v�Z��10.12> �ˁ@X�o�[�̏ꍇ��1.25�{
�@�EX�o�[�ƒ����l�̕W�{���z�ɂ��Ă�Figure 10.5���Q�ƁB
�������Ŏ����ꂽ�悤�ɁA���ϒl��p�����������x���������߁A�����l�������ϒl��estimator�Ƃ��ėp������B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i����j
�f�B�X�J�b�V�������R�����g
�ERelative efficiency �ɂ��āA���ϒl��p�����@�����x�������i�����l���g�p�����������U���L�����Ă��܂��̂Łj���߁A�����l�������ϒl��estimator�Ƃ��ėp������B
�E���U�����߂�ۂ�n-1���g���鍪���Ŗ��m�Ȃ��̂͂Ȃ��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����j
�y�[�W�g�b�v�ɖ߂�
2007/10/13
Chapter 11 �O�� (pp.255-264)
11.1 Introduction
���啔���̎��ؓI�����i�s���Ȋw�j�ł́A��������E��Ԑ��肪�g�p����A��Ԑ���ł̍l�����̑�������������ɂ����Ă����S�I�Ȗ������ʂ����B
������ג��o�E�W�{���z�E�m���𗝉����邱�Ƃ���������ɂ͌������Ȃ��B
���ϑ��W�{�����W�c�ɂ��Ăǂ̂悤�ɐ����ł��邩�H
11.2 Statistical hypotheses and explanations
�����v�I��������̋N����F18���I�����AJohn Arbuthnot
�������(����)������O����ӂ݂�ƁA���v(�w)�ɂ���Ă��鎖�ۂ̊m��������o�����Ƃ͂ł��邪�A���v(�w)���ꎩ�͖̂{���I�Ɍ��ۂ̐�������߂�^���Ă͂���Ȃ��B
11.3 Statistical versus scientific hypotheses
���Q��ނ̋�ʂ��ׂ�����
�@�Ȋw�I�����F���_�I�ȍl���Ɋ�Â��đ�܂��ɗ\������錋�ʂɊ�Â��B
�A���v�I�����F����\�Ȗ���Ƃ����ڍׂȏ��Ɋ�Â��������B�����ꂽ���v�I�����͓Ƒn�I�ȓ��@�͂̌��ʐݒ肳���B���v�I�����͖��m�Ȃ�ϐ��̐��l�ɂ��Ă̋L�q�B
���@�A����ʂ��邱�Ƃ͏d�v�ł���A��ʐ��y�яd�v�����Ⴍ�A�ɍ��ׂȎ���ɂ����铝�v�I�����������邱�Ƃ͉\�ł���B
���Ȋw�I�����́A���ׂē��v�I�����K�v�Ƃ���킯�ł͂Ȃ��A���v�I�����ɂ��Ă����ׂĎ��p�I���邢��Ȋw�I���v�������炷�킯�ł͂Ȃ��B
11.4 Testing statistical hypotheses about ��
�����v�I�����͐^�U������ɂ����������B�������v��@�ł͉������_�؉\�ł��邩�A���p���ׂ����Ɋւ��Č덷��������B
���\11.2�@���S�Ă̓��v�I��������ɕK����4��step�F
�@�@�������q�ׂ�A�A�댯���ݒ�i��= .05�j�A�B�m�������߂�A�C����
11.5 Testing H0: �� = K, A one-sample x-test�@�c�@�\11.2�̎���
�@�@����(H0)�F�{�q��IQ���ϒl�́A��ʂ̎q��IQ���ϒl(��= 100)�Ɠ����ł���B
�@�A�댯���F�� = .05 �i�ʗႱ�̒l�j
�@�B����ג��o�ŗ{�q(n = 25)��IQ���ϒl = 96.0�B
�@�@����(H0)=100�ł���A�m��( p )�̓�=100�𒆐S��4�Ȃ�������ȏ�قȂ�W�{���ςƂȂ�m���Ɛݒ�B
�@�C�m��( p ) < ��( .05)�ł���A����(H0)�F��=100��.05�̗L�ӊm���Ŋ��p�����B
�@�@���@�W�{���� = 96.0�̏ꍇ�͂ǂ��Ȃ邩�H
��national test norms�ɂ���=15�ł���̂ŁAn=25�̎��̕��ϒl�̕W�����z�ɂ�����SD�͎�10.1����3.0�B
����11.1�����Ƃ�z�l�����߁A����𐳋K�Ȑ��\�Ō��邱�ƂŕW�{���ς�96.0���邢�͂���ȉ��ł���m�������܂�i�A�����������p�ł��Ȃ��ꍇ�B�j�B
11.6 Two types of errors in hypothesis testing
���������������ɂ��S��炸�A���̉��������p���Ă��܂����Ɓ���P��̌��(��)
���������������Ȃ��ɂ��S��炸�A���̉������̑����Ă��܂����Ɓ���Q��̌��(��)
�����������p���邱�Ƃ͂��̉������u�������Ȃ��v�Ƃ������Ƃ��ؖ����Ă���킯�ł͂Ȃ��B100%�̊m�M�������ĔF�߂��鉼���ȂǂȂ��̂ł���B
11.7 Hypothesis testing and confidence intervals
���M����Ԃ͂����炭�������̐������v��@�ɍł��𗧂�(Tukey, 1960, p.429)
����Ԑ���ɂ��A�ϐ�����̐��m�x���������F�ʂɂ��Ẳ������茋�ʂɂ��ėe�Ղɔ��f���������Ƃ��ł���B
��.99�̐M����ԓ��ɓ��v�I�����ɂ���ē��肳�ꂽ�ϐ��l���܂܂�Ȃ���A���̉�����.01�ɗL�ӊm���Ŋ��p�����Əq�ׂ�ɓ������B
11.8 Type-�U error, ��, and power
������(H0)���x���i���p�ł��Ȃ��j�Ɣ��f����̂͊ԈႢ�ł���i���Ƃ��Ύ��ۂ̓ʁ�100�ł���̂Ƀ�=100�ł���ƌ��_�Â��Đ������Ȃ�H0���̑����Ă��܂��j
����Q��̌��
11.9 Power
�������{���̓�=110�ł���Ƃ�����H������(H0):��=100�ł���ꍇ�ɂ́A�ʁ�100�ł���Ƃ��ĉ����͊��p�������Ƃ���c�B�ł́AH0�����p�ł���m���́H
�����ł���H0�����p����m�������v�I����̌��o��(power)
11.10 Effect of �� on power
������(H0)�F��=100�A�Η�����(H0)�F�ʁ�100��������(��=.10)�ꍇ�́A���o�͂̓�=.05�̎���苭���B���}11.2
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����j
�f�B�X�J�b�V�������R�����g
�E�L�Ӑ�����ł́A���ؖړI�ŗ��Ă��Η������ƋA�������͍������₷���B�u��P��̌��v�́A�A���������^�ł���̂Ɋ��p�����i�܂�A�L�ӂ��Ɣ��f�����j�ꍇ�A���Ɂu��Q��̌��v�͋A�����������p�ł���i�܂�A�L�Ӎ�������j�̂ɁA���p���Ȃ������ꍇ�B
���v�������ʂ𑼂̐l�Ƒ��k�������Ƃ����A�_�_���A�������Ȃ̂��Η������Ȃ̂��A��Ɋm�F�������ĂȂ��ƁA����������₷���̂Œ��ӂ������B
�EPower�i���o�́j�����ׂĂ����ƁA�W�{���s���������ŗL�Ӑ��������Ƃ��Ă��Ȃ���������ڈ��ƂȂ�B���Ɍ��s�̌����ʼn����𗧏�����Ȃ��Ă��A����̕W�{���m�ۓ��A�����f�U�C���̉��P�ւ̎Q�l�ƂȂ邩������Ȃ��B�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����A����j
�y�[�W�g�b�v�ɖ߂�
2007/11/30
Chapter 11 �㔼 (pp.264-276)
11.11 Power and the value hypothesized in the alternative hypothesis
���s���w�̌����ł́A�p�����[�^��1�̐��l���牼���̌���͂��Z�o���邾���ŏ\���ł���A�Ƃ������Ƃ͂܂��Ȃ��B�ʏ�A�������̈قȂ�p�����[�^�̒l��p���Č���ׂ͂�B����͂́A(a) reasonable�ȁA�����Ƃ��傫���p�����[�^�l�A(b) practical�ȋ�������A�ł��������p�����[�^�l�A(c) �ł�reasonable�ȗ\���� "best guess" �Ȓ��Ԃ̒l�A�ɂ���Č��肳��邱�Ƃ������B���̒l���g�p�����Ƃ��ɂ́AFigure 11.4�̃O���t���\�z�����B
�����ۂ̃ʂ̒l�Ɖ��肳�ꂽ�ʂ̍����傫���Ȃ�قǁA����͂͑���1.00�̒l�ɋ߂��Ȃ�B�܂��A�ǂ̂悤�ȃʂ̒l�ł����Ă��A�T���v���T�C�Y���傫���Ȃ�قnj���͂��傫���Ȃ�B
���ʏ�A�����I�Ȓ��ōő���̃T���v�����Ƃ�A���̃T���v�����ŏ\���Ȍ���͂����邩�ǂ��������肵�Ȃ����Ə��������ł��낤�B�����T���v�������ƂĂ��傫���ċA�������̌���͂����ɑ傫���̂ł���A����Ȃɑ傫�ȃT���v�������g���K�v�͖����B�A���A�M����Ԃ͑傫�ȃT���v�������g���Ώ������Ȃ�B
���� = .05�̂Ƃ��Ɍ���͂�.90�ȏ�Ȃ̂��]�܂����B
11.12 Methods of increasing power
���������̎菇�ł́A�ȉ��̂��Ƃ������Ă���B
�@(a) ����͂̓T���v���T�C�Y��������قǍ����Ȃ�
�@(b) ����͂̓���������i��F.05����.10�Ɂj�قǍ����Ȃ�
�@(c) ����͂́A�e�X�g�����p�����[�^�̐^�̒l�����肳��Ă���l���������ƍ����Ȃ�B
������������ł́AType I error��.10�܂ő傫�����Č���͂��グ�邱�Ƃ��l���������悢�B
11.13 Nondirectional and directional alternatives: Two-tailed versus one-tailed tests
���Η������ł���H1��nondirectional (two-tailed) �ɂ�directional (one-tailed)
�ɂ����肤��Bnondiretional�Ȃ��̂́A�ʂ�0�ł͂Ȃ����A0���ォ���������y���Ȃ����̂ł���B����A��
> 100�Ƃ����Η�������directional�ł���A�����҂̓ʂ�100�ȉ��ɂ͂Ȃ蓾�Ȃ��Ɖ��肵�Ă���B
�����̏ꍇ�A�ʂ�100�ȏ�ɂȂ�Ƃ��̂A�����������p�ł��邽�߁A���p���邽�߂ɂ�sampling
distribution�̉E���ɖ�����Ȃ�Ȃ� (Figure 11.5)�B
��Figure 11.3��Figure 11.5���r����ƁAdirectional�ȏꍇ�̕�������͂��������Ƃ��킩��B
���������s���O��directional�ȑΗ�������p����Əq�ׂȂ���ΐ���Ȃ��Bdirectional�ȑΗ�������p�����ꍇ�A���ۂ�Type
I error�̊m����.05�ł͂Ȃ�.10�ł���Bdirectional�ȉ�����������������ɂ͈ȉ��̂悤�Ȃ��̂�����B
�E�����̔F�m�\�͂̔��B��IQ��������
�E10�Ύ���8�Ύ������s�A�m�̏�B���������@�@�ȂǂȂ�
11.14 Statistical significance verses practical significance
���T���v���T�C�Y���ƂĂ��傫���ꍇ�A�ق�̏����̈Ⴂ�ł��L�ӂȍ��ɂȂ��Ă��܂���������Ȃ��B�u���v�I�ɍ�������v�Ƃ����̂͋��R�ŗ\�z�������������傫���Ƃ������Ƃ��Ӗ�����݂̂ł���A���̍����傫��������d�v�������肷�邱�Ƃ���������킯�ł͂Ȃ��B
���L�Ӑ�����͔��ɗ���ɂ���Ă���B�L�Ӑ�������s���Ƃ��ɂ́A�M����Ԃ����������ǂ��ł��낤�B�M����Ԃ���邱�ƂŋA������������Ċ��p���Ă��܂��\�������炷���Ƃ��ł���B
11.15 Confidence limits for the population median
����W�c�̒����l�̐M����Ԃ�random sampling��n���猈�肳���B
11.16 Inferences regarding �� mean when �� is not known: t versus z
������I�ȖړI�ŁA�������̊T�O����@��z-test�ŕ\����Ă����B�������A�����Ђ̒l���킩��Ȃ��ꍇ�At-ratio�ƌĂ��
(z-ratio�ł͂Ȃ�)�B����n�̒l���傫����Ђ̒l�͂ƂĂ����m�ɂȂ�t��z�̍��͂قƂ�ǂȂ��Ȃ�B�������An���������ꍇ�ɂ�t��z�͂��Ȃ�قȂ�B���K���z�Ƃ͈قȂ�At���z��1�����ł͂Ȃ��B���R�x�iv�j�ɂ����t���z�͈قȂ�B
11.17 The t-distribution
��t���z��0�ςƂ��Ă��čŕp�l��1�̍��E�Ώ̂Ȑ}�ł���Bz���z�̕��U��1�����At���z�̕��U��1���傫���it���z�̕��U��v/(v-2)�ł��邽�߁j�Bv���������Ƃ��ɂ�t���z�̐�x���傫���Ȃ�i�܂蕽��ɂȂ�j�B�]���āA���̂悤�ȏꍇ�ɂ�5%��|t| = 1.96���傫���Ȃ�B
��v�����Ȃ�傫���Ƃ��ɂ�t���z�͐��K���z�Ɠ����ɂȂ�iFigure 11.6�Q�Ɓj�B�܂��AFigure
11.7��t��critical value�Ǝ��R�x�̊W��\�������̂ł���Bv��������t�̒l��z�̒l�̋߂Â��B
11.18 Confidence intervals using the t-distribution
���Ђł͂Ȃ�s��p�����ꍇ�̕����M����Ԃ����L���Ȃ�B
11.19 Accuracy of confidence intervals when sampling non-normal distributions
��Figure 11.3�ɂ���ʂ�A�T���v������5�l�ł��M����Ԃ͂��Ȃ萳�m�ɂȂ�B
11.20 Chapter summary
���������͐������v�ōł��ǂ��g������@�ł���B�������ł͊ϑ����ꂽ�����A�A�����������傫�����ǂ����̉\���ׂ�B���̉\����5%��菬������A�������͊��p�����B���p����Ȃ��ꍇ�A����̌��͋N����Ȃ����A����̌�肪�N����\��������B����̌��Ƃ́A�{���͊��p���ׂ��A�����������p���Ȃ��Ƃ������̂��Ƃł���B
������̌��̊댯�����Ȃ��قǁA����̌��̊댯�������Ȃ�B�t�ɁA��
= .10�̎��ɂ́A�� = .05��.01�̂Ƃ���������͂������B����̌���Ƃ��Ȃ����Ƃ�����͂Ƃ����B����͂̓T���v���T�C�Y�������Ƒ�����B
�����K���z��1���������At���z�ɂ͂�������A���R�x�ɂ���ĕς��B
���L�Ӑ�����ł͈Ⴂ�̑傫���͂킩��Ȃ����A�L�Ӎ�������ƕ�����Ȃ���A�ǂ�Ȏ�ނ̗L�Ӑ������邩�ǂ����͂킩��Ȃ��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(�X�{�j
�f�B�X�J�b�V�������R�����g
�E����͂Ƃ͍�������Ƃ�����m����\���B
�E��x���傫���Ȃ� (leptokurtic) �ƃJ�[�u���}�ɂȂ�킯�ł͂Ȃ��̂��H�����̒�`���Ɛ�x���傫���Ƃ͕��ϒl�̕ӂ�ɏW�����Ă��镪�U��\���A����Ă��邱�ƂɂȂ�͂��ł��邪�A���̒�`���Ɩ{���ƍ���Ȃ��č��������B�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�C�j
�y�[�W�g�b�v�ɖ߂�
2007/12/21
Ch. 12. Inferences about the difference between two means.
12.1 Introduction
���@�������v�̍l�@�͈ȉ��̒i�K�ށB
�E�A���������q�ׂ�
�E�O����q�ׂ�
�E���v��@�m�ɂ���
�E�T���v���̕��z���`����
�E�L�Ӑ������߂�
�E�M����Ԃ��߂�
�E����������
�E�i��������j���̑����ʂɍl�����邱�Ƃ��q�ׂ�
12.2 Testing statistical hypotheses involving two means
���@Ch. 11�ł̓� = k�Ƃ����A�������ɂ��Ĉ��������A2�̕��ϒl�̍��ɂ��Ă̂ق�����苻���[���itreatment�����ʓI���������A�Ȃǁj�B
12.3 The null hypothesis, H0: ��1�|��2��0
���@12.2�ŋ���������ɑ���A�������̓�1 = ��2�������̓�1�|��2��0�ł���B
12.4 The t-test for comparing two independent means
���@����O���[�v�����ʂ�treatment���A����1�̕ʂ̃O���[�v���Ȃ������ꍇ�A2�̃O���[�v�͓Ɨ����Ă���Ƃ�����B�������A����O���[�v��pretest��posttest���ׂ�ꍇ��paired�ł������葊�ւ����邽�߂ɁA�Ɨ����Ă���Ƃ͂����Ȃ��i����ɂ��Ă�12.13�ň����j�B
���@�A�������̓�1�|��2��0�ł���A�Η������̓�1�|��2 �� 0�ł���B
���@���U�̓������Ɗe�T���v�������ꂼ��̕�W�c���烉���_���Ɏ��o����Ă��邱�Ƃ��O��ł���B
���@�A��������p. 285�̏�̎��Ōv�Z�����B�p�����[�^�͈��ł��邽�߁A�p�����[�^�ƃT���v����SD�̍��́A�T���v����SD�Ɠ����ł���B�]���āA���̎���Sstatistics��t�ŕ\�����B
���@z-ratio�ƈقȂ���t-ratio�̓p�����[�^�ł͂Ȃ��T���v���ɂ��Ăł���B�]���āAt-ratio�ł�sampling error�͕���ɂ����q�ɂ��e������B
���@t����̎���12.1�̒ʂ�B
12.5 Computing S�iX�o�[1�|X�o�[2�j
���@s2��SS/df�ŋ��߂���B
12.6 An illustration
���@���̎h�����c���̒m�\��L���邩�ǂ����ɋ���������Ƃ���B18���̗c���������Q�ŁA����18���������Q�ł���B2�N��ɂ���36���̗c���ɑ��Ēm�\�e�X�g���s�����B
���@Table 12.1�ł͋A�������͊��p����Ă��Ȃ��B�������A10%�����ɂ���Ɗ��p�����B�܂��At����̕���̓T���v���T�C�Y�ɑ傫���e�������B�T���v���T�C�Y���傫���Ȃ�Ε��ꂪ�������Ȃ邽�߁A�T���v���T�C�Y���傫���Ə����ȍ��ł�t�l���傫���Ȃ�B
���@t�l���L�Ӑ����̒l������A�������͊��p����邪�A�����Ȃ����Type II error���N����BType I error��Type II error�̓g���[�h�I�t�̊W�ɂ���B
���@p�l�ɂ��ẮA�Ȃ�ׂ����m�ɕ���̂��ǂ��ł��낤�Bp > .05�Ə�������.10 > p > .05�Ə����ق����]�܂����B
12.7 Confidence intervals about mean differences
���@95%�M����Ԃ̒���0���܂܂�Ă���ƁA�A�����������p�ł��Ȃ��B�����-.89����20.29�̊Ԃɂ��邽�߁A���p�ł��Ȃ������B
12.8 Effect size
���@���ʗʂ͍��̑傫���ׂ�̂ɗL���ł���B12.7A, 12.7B���ŋ��߂���B
12.9 t-test assumptions and robustness
���@t����ɂ�����3�̑O��́A���K���z���Ă��邱�ƁA�����U�ł��邱�ƁA���ꂼ��̃T���v�����Ɨ��ł��邱�ƁA�ł���B
���@���K���z�ɂ��ẮA���������p����ΐ��K���z�����Ă��Ȃ��Ă��قƂ�nj��ʂɕς��͂Ȃ����Ƃ������Ă���B�T���v���T�C�Y���傫����i15�ȏ�j�Atype I error�̈Ⴂ��1%�ȓ��ɂ����܂邾�낤�B�܂��AType II error�ɂ��Ă��A���K���z���Ă��Ȃ��Ă��e������Ȃ��B�]���āA���K���z�ɂ��Ă͗�����t�����p����ΕK�v�ȑO��ɂ͂Ȃ�Ȃ��B�Б�����̏ꍇ�ɂ́A�T���v���T�C�Y���������O���[�v�ł���20���͕K�v�B
12.10 Homogeneity of variance
���@t����͓����U���ɂ��Ă��挒�ł���Ƃ����Ă���B���ɁA�T���v���T�C�Y��2�Q�̊Ԃœ����̏ꍇ�ɂ͖��ɂȂ�Ȃ��BFigure 12.3�ɁA�T���v���T�C�Y�������Ƃ��ƈقȂ�Ƃ��̃O���t���f�ڂ���Ă���B
���@2�Q�̊ԂŃT���v���T�C�Y���傫���O���[�v���A���U���傫����W�c������o����Ă����ꍇ�ɂ́At�����Type I error�ɑ���conservative�ɂȂ�B����A�T���v���T�C�Y���傫���O���[�v�����U����������W�c������o����Ă����ꍇ�ɂ́AType I error��Ƃ��m�����������Ȃ�B
12.11 What if sample sizes are unequal and variances are heterogeneous: the Welch t' test?
���@�T���v���������U���قȂ�ꍇ�ɂ́AWelch t'-test��p���邱�Ƃ��ł���Bt'�̒l�͒ʏ��t�̕\����ǂݎ�邱�Ƃ��ł���B�����U�������肳��Ȃ��ꍇ�At'��t������⌟��͂��ア�B
12.12 Independence of observations
���@�Ɨ������O���[�v�Ƃ����̂́A2�Q��paired����Ă��Ȃ�������A���ւ��Ȃ�������A�֘A���Ȃ��A�Ƃ������Ƃł͂Ȃ��B��������̊W��2�Q�ɂ���̂ł���Adependent��t�����p����ׂ��ł���B����independence of observation�͏d�v�ł���B���ꂪ�Ȃ���AType I error��Type II error�̊m���͐��m�ł͂Ȃ��Ȃ�B
12.13 Testing��1�@=��2 with paired observations
���@���܂Ō��Ă���t����ƈقȂ�̂́A���ς̈Ⴂ�̕W���덷�Ǝ��R�x�ł���B
���@�T���v�����m�ɑ��ւ����邱�Ƃ����肳��Ă���i�����q����1�N��A�j�̎q�����Ƃ��̎o�������A�v�ƍȂȂǁj�B
���@paired t-test��independent t-test��������͂������B
12.14 Direct-difference method for the t-test with paired observations
���@�����Q�ɂ��Ĕ�ׂ�̂ł���A�����\�͂̊w����posttest�ł��������_����邱�Ƃ��\�z�����B���̂悤�ȑ��ւ��l������Ă���B�������邱�ƂŌ���͂��オ��B
12.15 Cautions regarding the matched-pair design in research
���@paired t-test��p��������Ƃ����āA���S��2�Q����������Ă���킯�ł͂Ȃ��B
12.16 Power when comparing means
���@���ʗʂ̌���́ipower for effect size�j�ɂ��ẮA.2�Ђ�small, .5�Ђ�middle, .8�Ђ�large�ƌ����Ă���B�l�X�ȏ�ʂɂ�������ʗʂɂ��Ă�Table 12.4�Ɍf�ڂ���Ă���B
���@����power�͎������v�悷��Ƃ��ɐ��肳��Ă���ׂ��ł���B
12.17 Non-parametric alternatives: The mann-whitney test and the wilcoxon signed rank test
���@Mann-Whitney test��2�̓Ɨ������Q�ɑ��Ďg�p����B���̕��@�́A���K���z���Ă��Ȃ��Ƃ��ɗǂ��g�p����Ă������At���肪���K���z���Ă��Ȃ��Ƃ��ł��挒�������邱�Ƃ��킩���Ă���́A���܂�g�p����Ȃ��Ȃ����B���ɊO��l������ꍇ�ɂ�Mann-Whiteney�͂��܂�悭�Ȃ����߁AWelch t' test��p�������������B
���@Wilcoxon signed rank test��paired sample�̂Ƃ��ɗp������BWilcoxon��t-test�����D�܂�Ă��邪�A����t-test�������N�Ōv�Z���ꂽ��A�T���v���T�C�Y�����ɏ������Ȃ�����A���ʂ͂قƂ�Ǖς��Ȃ��B
�f�B�X�J�b�V�������R�����g
�Et����ł̓T���v���T�C�Y���傫���Ȃ�ƁA�L�Ӎ����o�₷���Ȃ邱�Ƃ����������B
�Ep > .05�Ə��������]�܂����Ƃ��������A����p = �Ɛ��m�Ȓl�������ꍇ�������̂ł͂Ȃ����B�܂��Ap = .000�ƂȂ������͂ǂ̂悤�ɋL�q����ׂ����H
�E12.13�ŃT���v�����m�ɑ��ւ�����ꍇ�́Apaired���g���B����͂������Ƃ����̂͗L�ӂɂȂ�₷���Ƃ������ƁB
�E12.16�̂Q�ЁA�T�ЁA�W�Ђ̒l�͂ǂ����痈�Ă���̂��H�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�C
�y�[�W�g�b�v�ɖ߂�
2008/ 01/11
Ch. 13 Statistics for categorical dependent variables: Inferences about proportions
13.1 Overview
���@�����Љ�Ȋw�̕���ł́A���� (proportion) �ɂ��Ă�RQ�������B�{�͂ł͊����ɂ��Ẳ������ɂ��Ă̐�����@�ɏœ_�Ă�B�����́Acategorical, nominal�ȕϐ����r����Ƃ��ɗp�����邱�Ƃ������B
13.2 The proportion as a mean
���@�T���v������n�̂Ƃ��A�������̓������������T���v����ni�Ƃ���B���̏ꍇ�An�̒���ni�̊�����p = ni / n�ŕ\�����Bp�̓i��W�c�ɂ����邠�����̓��������������ۂ̊����j��estimator�ł���i�܂�A�T���v������̐��肪p�j�B
13.3 The variance of a proportion
���@������J�e�S���[�ɂ�����1�Ƃ��ꂽ���ۂ̊������Ƃ���ƁA����dichotomous variable��SD��13.3���̒ʂ�ɂȂ�B���̂悤�ȕϐ��͐��K���z�ɂ͂Ȃ�Ȃ��̂ŁASD�͕`�ʓI�ɂ͗p�����Ȃ����Ap�̕W���덷����������@��1�i�K�ɂ͂Ȃ�B
13.4 The sampling distribution of a proportion: The standard error of p
���@�p�x���z���ǂ�Ȍ`�ł��낤�ƁAsampling distribution of the mean�̓T���v���T�C�Y���傫���Ȃ�Ɛ��K���z�ɋ߂Â��iFigure 10.3�j�B�Ⴆ�A���������������_����100���̃T���v�������̓x�ɑI��ōs���ƁA������p�̒l�͐��K���z�ɋ߂Â��A����p�̒l�̓ɋ߂��Ȃ�B����sampling distribution��proportion�̕W���덷�ƌĂ��B
13.5 The influence of n on ��p
���@100���̑����400����������ǂ��Ȃ邾�낤�BFigure 13.2�ɂ��ƁA4�{�ɂ���ƃ�p�͔����ɂȂ�B
13.6 Influence of the sampling fraction on��p
���@��W�c����T���v���Ɏ���������if�j�̓�p�ɂǂ��e������̂��낤���B��W�c��5%�ȏ���T���v���Ƃ��Ď�����ꍇ�ɂ́A���ʂɂقƂ�LjႢ�͖����B���ۂɂ�N�͂قږ�����ł���B
13.7 The influence of �� on ��p
���@��p�̓̒l�ɂǂ̂悤�ɉe�������̂��낤���B�W���덷�̍ő�l�̓�.5�ł���Ƃ��ł���B�T���v���̕��z�̓�.50�̂Ƃ��Ɋ��S�ɍ��E�Ώ̂ɂȂ�A�����łȂ���skewness�������B
13.8 Confidence Intervals for ��
���@n��������Ɛ��K���z�ɋ߂Â��B�������A�ǂ̒��x��n���K�v�Ȃ̂��낤���B�T���v���T�C�Y�ɂ��Ă͗l�X�ȃK�C�h���C�������邪�A�����̊�͑e������B95%�M����Ԃ邽�߂̃T���v���T�C�Y�̓ɑ傫���e�������B�}13.4�ɂ��ƁAp��.40����.60�̎��ɂ�50�l�ȉ��ł��������A.20�ȉ���.80�ȏ�̎��ɂ͔��ɑ傫�ȃT���v���T�C�Y���K�v�ɂȂ�Bbimodal�ȂƂ��ɂ�Ghosh (1979)�̕��@���ƂĂ����m�ŁAp��n�̒l��I�ԂƂ��Ɏg�p�ł���B
13.9 Quick confidence intervals for ��
���@�}13.5��p����Α�̂̐M����Ԃ�������B�Ⴆ��p��.9��n��10�̎��ɂ�58%����98%��95%�M����Ԃł���B
13.10 Testing H0 : �� = K
1. �����铝�v�I�ȋA�������́A��������������Ă���̊�����K�Ɠ����ł���A�Ƃ������̂ł���B
2. �A�������̌��ɂ́An����W�c���烉���_���ɑI�ꂽ�A�Ƃ����O����݂̂ł悢�B
3. �A��������z����Ō������B
4. 13.9���̒l�����p��Ɣ�r�����Bn��p�̐��K�������肳��Ȃ���A�J�C����goodness-of-fit test���p������B
5. 13.8A-B���Ń̐M����Ԃ����߂���B�T���v���T�C�Y���\���ɑ傫�����K�������������A95%�̐M����Ԃ́}1.96��p�ŋ��߂���B
13.11 Testing empirical versus theoretical distributions: The chi-square goodness-of-fit test
���@�J�C��挟���2�ȏ�̊ώ@���ꂽ�������L�ӂɈقȂ�̂��ׂ邽�߂̃e�X�g�ł���B�t�^��Table D�ɃJ�C���̊��p�悪������Ă���B�J�C����p����ۂ̎��R�x�́A���̃J�e�S���[���}�C�i�X1�ł���B
13.12 Testing differences among proportions: The chi-square test of association
���@2�̂��̂̊֘A�ׂ�ꍇ�i��F�^�o�R���z�����ǂ����ƐS���a�Ƃ̊֘A�j�A���R�x�� (row-1) �~ (column-1)�ɂȂ�B����2�Ɋ֘A�������ꍇ�A�c�̗���̊e�Z���̊����͂��܂���Ȃ����낤�B�A�����������p���ꂽ��A2�̕ϐ��̊ԂɂȂ�炩�̊W��������Ƃ������Ƃł���B
13.13 Other formulas for the chi-square test of association
���@�J�C��挟����s���̂ɂ͑��́A�����ƒ��ړI�ȕ��@������B
13.14 The ��^2 median test
���@9�i�K��rating�ŁA�����l����̓��_�������������j���ňقȂ邩�ǂ������J�C��挟��Œ��ׂ邱�Ƃ��o����B�������At����̕�������͂������B������median test��3�ȏ�̃O���[�v���r���邱�Ƃ��o����B
13.15 Chi-square and the phi coefficient
���@�J�C���̓��v��test of association��phi �i�Ӂjcoefficient�̒l�ɗe�Ղɕϊ��ł���i�C�`�[���̂悤�ȓ�i�@�̃f�[�^�ŎZ�o����Pearson product-moment coefficient��phi coefficient�ƌĂ��c���삳���ch. 7�̃n���h�A�E�g���j�B
13.16 Independence of observations
���@�J�C���͑��̊ϑ��ƓƗ����Ă���contingency table�ł���ǂ�Ȃ��̂ɂ��g�p�ł���B�����ł����Ɨ����Ă���Ƃ́A���ݔr���I�ł���Ƃ������Ƃł���i�����l�������̃J�e�S���[�ɓ������肵�Ă��Ă͂����Ȃ��j�B
13.17 Inferences about H0: ��1 = ��2 when observations are paired: McNemar's test for correlated proportions
���@�f�[�^��paired�̏ꍇ�ɂ́AMcNemar's chi-square test���g�p���邱�Ƃ��ł���B
�f�B�X�J�b�V�������R�����g
�E Skewness�̌������B��(positive or negative)�ɂȂ肪���Ȃ̂ŁA������x��������Ɣc������K�v������B
�E �ԓ��median test�̍��ł��q�ׂ��Ă��邪�A�ꍇ�ɂ���Ă�t����̕�������͂��������Amedian
test��3�O���[�v�ȏ���r���邱�Ƃ��ł���ȂǁA���ꂼ��̓������l��������ŁA���m�Ȏg���������K�v�ł���Ɗ������B�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@����
�y�[�W�g�b�v�ɖ߂�
2008/01/25
Ch. 14 Inferences about correlation coefficients
14.1 Testing statistical hypotheses regarding ��
���@�T���v���ɂ����鑊�W���ir�j���L�ӂ��ƌ����ɂ͂ǂ�����悢���낤���B�܂�H0�̃ρi�ꐔ�ɂ����鑊�ցj = 0�͂ǂ̂悤�Ɍ��ł���̂��낤���Br��0��������H0�͊��p���ꂸ�A0�łȂ���Ί��p�����̂��낤���H
���@����ɂ͌덷�������̂ł��邽�߁A�������ł͂����Ȃ��B�ς��{����0�ł�r��.5��.6�̂��Ƃ�����B�T���v���T�C�Y���ƂĂ��������Ƃ��ȊO�ɂ͂����炭����Ȃ��Ƃ͂Ȃ����낤���A�ł��\���͂���i�R�C���̕\��10��A���ŏo������A�Ƃ����Ӗ��ł̉\���j�B�܂�A�ς�0�ł�r�̓v���X�}�C�i�X1�͈͓̔��̒l����蓾��B�]���āA�T���v������̒l�ł���r����ςɂ��Ă̐�ΓI�Ȋm�M�������Ƃ͂ł��Ȃ��B����́A���v��p����Ƃ��ɂ͏�ɕt���܂Ƃ����ł���Ba risk of making an incorrect decision is always present!
���@�D�P���̑̏d�̑���X�ƁA�o���̏dY�̊W��658�l�̐V�����ɑ��Ē����������ʁA���ւ�.212�ł������B.212�Ƃ����l��0����傫����������Ă���킯�ł͂Ȃ����A�T���v���T�C�Y�͔��ɑ傫���B�ł́A����덷��L����x�܂ނ悤�ȓ��v�����W�c�̕ϐ����ǂ̂悤�ɐ��肷��悢�̂��낤���H�{�͂ł́A����𑊊ւɑ��ĉ��p����B
14.2 Testing H0: �� = 0 using the t-test
���@t������s���Ƃ��̎��R�x�́Apairs of score��n�Ƃ����Ƃ��A�� = n-2�ł���Bt����ł̂�����pp. 350-351�̒ʂ�Br��critical value�̃O���t��p. 352��Figure 14.1�Ɍf�ڂ���Ă���Bn���������r��critical value����������B�܂��A�����������Ƃ��ɂ͂��傫��r�̒l���K�v�ƂȂ�B���̐}�́A����r��critical value�ɑ���T���v���T�C�Y�̑傫�������肷��Ƃ��ɂ��g�p�\�ł���BAppendix��Table J���Q�Ɖ\�ł���B
14.3 Directional alternatives: "Two-tailed" vs. "one-tailed" tests
���@�� = 0 �Ƃ����A�������͕Б�����ł���������ł��\�ł���B��������̏ꍇ�̓� > 0�ł��� < 0�ł��A�����������p�ł���B������ > 0�ƃ� < 0�̂ǂ��炩���s�����ł���ꍇ�ɂ͕Б������p���邱�Ƃ��ł���i��̑傫���Ƒ��̑傫���̑��ւ̏ꍇ�Ȃǁj�B
���@�Б������p����ꍇ�ɂ͂�������l���Ȃ���Ȃ�Ȃ��B�Ȃ��Ȃ�A����1000���̃T���v����r��-.9�̂Ƃ��ł��A�ρ�0�Ƃ����Б�����ł̓ς�0�Ƃ������ƂɂȂ��Ă��܂�����ł���B�������A�K�Ɏg���ΕБ�����͂�茟��͂�����B
���@��>0�Ƃ����Б������p����Ƃ��ɂ́A��>0�Ƃ����m�����K�v�Ȃ킯�ł͂Ȃ��B�ς����̒l�ɂȂ�Ƃ������Ƃ�unreasonable�ł���Ƃ������Ƃł悢�B�������A���ւ̏ꍇ�ɂ͗�������̕�����葽���g�p����Ă���B
14.3 Sampling distribution of r
���@�ςɂ�����r�̕��z�́A�ς�0�łȂ�����͐��K���z�ɂȂ�Ȃ��B5�g�̈ꗑ���o�����̐g���̑��ւ�.95�̏ꍇ�A.99�̑��ւ̏ꍇ�����邵.50�̏ꍇ�����肤��i�v���X�}�C�i�X1�ȓ��̒l�������Ȃ����߁A�����̂ق��������傫���Ȃ�j�BFigure 14.2�ɃO���t���f�ڂ���Ă���B
���@���z���䂪��ł���ꍇ�A�ʏ�̐M����Ԃ̐���ł͐��m�Ȓl���Z�o����Ȃ��B�T���v���T�C�Y��������قǐ��K���z�ɋ߂Â��BFigure 14.3�̓T���v���T�C�Y��10������160���̂Ƃ��̃O���t�ł���B
14.5 The Fisher Z-transformation
���@Fisher�̓ς�n�Ɋւ�炸�Ar���قڐ��K���z�ɂȂ�悤�ɕϊ������lZ���l�Ă����B�����Z�ϊ��Ƃ����i�X�{���FExcel�ŊȒP�ɏo���܂��B����=FISHER()�j�BFigure 14.4��z�ϊ��̃O���t���f�ڂ���Ă���B
14.6 Setting confidence intervals for ��
���@Z�ϊ��ɂ���āAr�̐M����Ԃ��o���ۂ̖�肪�������ꂽ�B95%�M����Ԃ̓�z�Ɂ}1.96�������AZ���ɑ��������̂ł���i�X�{���F�ȒP�ɏo����悤�ɂȂ��Ă���Excel�̃V�[�g������j�B
14.7 Determining confidence intervals graphically
���@�ς�95%�M����Ԃ����߂�ɂ�Figure 14.6���g�p�\�ł���B
14.8 Testing the difference between independent correlation coefficients: H0: ��1 = ��2
���@�ꏏ�Ɉ�Ă�ꂽ�ꗑ���o�����ƕʁX�Ɉ�Ă�ꂽ�ꗑ���o������IQ��95%�M����Ԃ��߂��ꍇ�A����2��r�͗L�ӂɈقȂ�̂��낤���H���̂悤�ȏꍇ�ɂ�z�����p����B�v�Z����p. 360�̒ʂ�i�X�{���F���͂����Excel�Ɏ������čs���܂����j�B
14.9 Testing differences among several independent correlation coefficients: H0: ��1 = ��2 = �c=��J
���@14.8�ł̂�����2�̑��W���̏ꍇ�݂̂Ɏg�p�ł��邪�A3�ȏ�̑��W���̏ꍇ���v�Z�\�ł���B����p. 361�̒ʂ�B14.8�ł�14.9�ł����W����z�ϊ����Čv�Z���邪�A3�ȏ�̏ꍇ�ɂ̓J�C��挟��ƂȂ�B
14.10 Averaging r's
���@2�ȏ��r�ς������ꍇ�ɂ�Fisher��z�ϊ����s���Bz�ϊ������l�ς�����ϊ������ɖ߂��K�v������i�X�{���FExcel�̊��ł�=FISHERINV()�j�B
14.11 Testing differences between two dependent correlation coefficients: H0: ��31 = ��32
���@2�̑��W�����Ɨ����Ă��Ȃ��ꍇ�ɂ�14.10����p����B
14.12 Inferences about other correlation coefficients
���@���̏͂̎c��́A7�͂�8�͂ŏЉ�ꂽ�ق��̑��W���Ɋւ���L�Ӑ�������ȒP�Ɉ����B��������Ƃ��āA�A�������������ւƂ����Ƃ��Ɖ��肵�Ă����B
14.13 The point-biserial correlation coefficient
14.14 Spearman's rank correlation
14.15 Partial Correlation
14.16 Significance of a multiple correlation coefficient
14.17 Statistical significance in stepwise multiple regression
���@next best�ȏ]���ϐ����L�ӂɏd���W���������邩�ׂ�B
14.18 Significance of the biserial correlation coefficient
14.19 Significance of the tetrachoric correlation coefficient
14.20 Significance of the correlation ratio
14.21 Testing for nonlinearity of regression
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�X�{�j
�f�B�X�J�b�V�������R�����g
�����ւ̐��������肵�ė\���ł���ꍇ�ɂ͕Б������p���邱�Ƃ�����Ƃ���Ă��邪�A���炩�ɕБ��������肦�Ȃ��ꍇ�������āA���������p����悤���B
���W�{���������Ȃ邱�Ƃɂ���ėL�ӂȑ��ւ��o�₷���Ȃ�B�_�����ł́u�L�ӂȑ��ւ��������v�Əq�ׂ�ɂƂǂ܂炸�A���̒l����߁i�������ւȂ̂��A�����x�Ȃ̂��A�Ⴂ���ւȂ̂��j���q�ׂ邱�Ƃ��K�v���낤�B�܂��A�\�ł����95%�M����Ԃ����Ă����Ƃ���ɎQ�l�ɂȂ�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i����A����j
�y�[�W�g�b�v�ɖ߂�
2008/02/08
Chapter 15 One-factor analysis of variance
(pp. 377-395)
15.1
��analysis of variance
(ANOVA) ��J�� (J > or = 2) �̕��ϒl�̊Ԃ�sampling error�ɂ����̈ȏ�̈Ⴂ�������ǂ����͂��铝�v��@
15.2 �Ȃ�t������J��Ԃ��g�p���Ȃ��̂�
���� = .05��t�������x�s���ƁA���� .05�ł��邪�A2��ȏ��t������s���ꍇ�Atype-I
error�̉\���� .05���������Ȃ�B���̐��������Ȃ�قǁAtype-I error�̉\���������Ȃ邱�Ƃ����ƂȂ�B
���Ⴆ�AJ = 5�̂Ƃ��A�S�Ẵy�A�̑g�ݍ��킹��10�ʂ�ƂȂ� (k = 10)�Bp = 1 - (.95)10 = 1 - .60 = .40 �ƂȂ�B
��ANOVA�́u���肳���J�̕��ϒl�̂����A�ǂꂩ��ł��A���̑��̂ǂꂩ��̒l����sampling
error�ɂ����̈ȏ�قȂ��Ă��邩�v��₤���̂ł���B�����Ō������A��������
H0 = ��1 = ��2 = ��3 = �c = ��J
��t����ł͂Ȃ�ANOVA���g�p���闘�_��: (1)
type-I error���ɂ����A(2) �A�����������������p����� (�������ɕۂ����)�A(3) ������3�ȏ�̕ϐ��̉e�������肷�邱�Ƃ��ł���B
15.3 ANOVA�̐���
���Ⴆ��9������3�Q����ꍇ�Atreatment
factor��3���x�� (levels) ����Ƃ�����B���ꂼ��̋��͎҂�replicate�Ƃ����邽�߁A9 replicates for each of
the three levels of the treatment�ƋL�����Ƃ��ł���B���̗�̂悤�Ɋe�O���[�v�Ɋ܂܂��f�[�^���������ꍇ�Abalanced
design�Ƃ�����B
15.4 ANOVA�̌v�Z�@total sum of squares (SStotal)
���A�����������肷��ۂɁAsum of square (SS) �����p�����BSStotal��treatment effects��sampling error�Ȃǂ̑S�Ă̗v�� (sources of variation) �𑍍��������̂ł���B��v����ANOVA��SStotal�͓�̗v���ɕ��ނ����: between group means��within the groups�ł��� (SStotal = SSBetween + SSWithin)
15.5 sum of squares between (SSB)
��sum of squares between (SSB) �̓O���[�v�̕��ϒl�Ԃ̈Ⴂ�ɂ���Đ�����B��j �̓O���[�vj�̕��ϒl(��j) �ƑS�̂̕��ϒl (��) �̍��������Ă���B������j = ��j - ����treatment�̌��ʂ������Ă���B
��SSB �͌v�Z��15.4�ɂ���Ď�����Ă���B
15.6 sum of squares within (SSW)
��Group 1��SSW�̓�ixi12 = SS1�BJ�̃O���[�v��SSW��SS1 + SS2 + �c + SSJ
�܂��́ASSWithin = SStotal - SSBetween
��ANOVA�ł�F-test��p���Ă���B�v�Z�菇���}15.2 (p. 381) �Ɏ�����Ă���B
SSB��SSW���v�Z����A���ꂼ�ꂪ�X�̎��R�x (vB, vW) �Ŋ����AMSB��MSW���Z�o�����BMSB/MSW��F�l�Ƃ��Čv�Z����A���̒l��critical
F-ratio����������A�����������p�����B
��F�l�̃��X�g��Appendix��Table
F���Q�Ƃ̂��ƁB
15.7 ANOVA�̌v�Z��
���A���������������ꍇ�ASSB��SSW�̗\���l�͓�����: E(SSB) = E(SSW) = ��2�ƂȂ�
��critical value��central F-distribution�ɂ�����1-��th�p�[�Z���^�C�����ʂł���B
���Ƃ���63���̗c����3�Q�ɕ�����Ă���ꍇ�ɁA�� = .05�ł���Ȃ�A�ϑ����ꂽF�l�����R�x2��60�ł���F-distribution�ɂ�����95th
�p�[�Z���^�C���̒l���������Ȃ���Ȃ�Ȃ��B
15.8 ANOVA�̗��_
��ANOVA���_�ɂ��ƁAJ�̈قȂ�populations������A���ꂼ�ꂪ����������������U���������ꍇ�ɁAH0���x�������B�܂�قȂ�W�c�ł���Ɖ��肵�Ă���J�����ۂ͈�̕�W�c���璊�o���ꂽ�T���v���Q�ł��邱�Ƃ������B
15.9 Mean square between groups, MSB
����W�c�̕��U�̗\���l��mean square between�ƌĂ� (�v�Z��15.8A, p. 385)�B���Ȃ݂ɁA��̕�W�c����J�̃T���v�������o���ꂽ�ꍇ�A�����J�̃T���v���̕��U�̕��ϒl����2/n =��X-2
����W�c�̕��ϒl�ɂ��ċA������ (H0 = ��1 = ��2 = ��3 = �c = ��J) ���x�������ꍇ�AJ�̃T���v���̕��ϒl�Ԃ̍������2�����肳��� (unbiased estimate�ƂȂ�B�܂�A���Ғl�����肵�悤�Ƃ���ꐔ�ƈ�v����)�BnsX-2 = MSB����2�Ƃ�sampling error�ɂ�鍷�����Ȃ��A���x���J��Ԃ����Ƃɂ��sampling error�̕��ϒl��0�ƂȂ�B�����A������������Ă���ꍇ�ɂ�E
(MSB) >��2�ƂȂ�B
15.10 Mean square within groups, MSW
���A���������x�������ꍇ�AMSB��MSw�̗�������W�c�̕��U��unbiased estimate�ƂȂ�B�������AMSw��MSB�ƈႢ�A�A���������x�������ꍇ�����p�����ꍇ�ɂ��s�̊��Ғl�ƂȂ�B���������āA�A�����������p�����ꍇ�AMSB��MSw�����傫�Ȓl���Ƃ�ƍl������B
15.11 F����
��MSB/MSW�ɂ���ĎZ�o�����F�l��1�ɋ߂��ꍇ�A��������2�̐���l�ƂȂ�ƍl������B�ł́A1�����ǂ̒��x�傫���Ȃ�A�����������p���鎖���ł���̂��낤���H���̓�����15.7�ł��������ꂽ�Ƃ���AF = MSB/MSW��critical-F���������Ȃ����ꍇ�ł���B
15.12 balanced design��ANOVA
���e�O���[�v�Ɋ܂܂��replicates�̐� (n) ���������ꍇ�́A�������Ȃ��ꍇ�ŏd�ݕt�����K�v�ƂȂ�悤�ȏꍇ�ɂ���ׂČv�Z���e�Ղł���B
����v�Z�̕��@��pp. 386-388���Q�Ƃ̂���
15.13 A statistical model for the data
��ANOVA�ł́A�ǂ̃f�[�^�����`���f���Ŏ�������̂ł��邱�Ƃ����肵�Ă���B
�v�Z��15.10 Xij = �� + ��j + ��ij
Xij�̓O���[�vj�̐l��i�̓��_
���͕�W�c�̕��ϒl
��j��treatment j�̉e��������
��ij�͓��_Xij��error�������A���_Xij�̎c�� (residual) �ł���: ��ij = Xij - �� - ��j
��ANOVA�̖ړI�́A3��treatment�ɈႢ�����邩�A3�̕��ϒl�̊Ԃ�sampling
error�Ƃ��������傫�ȈႢ�����邩�����肷�邱�Ƃɂ���B
��sampling error�̋N���闝�R: (1) ���s��ꂽ�����̌��ʂ͕ʂ̃T���v�����g�p���Ď��{�������������Ƃ͈قȂ錋�ʂƂȂ�A(2)
���͎҂��悤�Ɉ������ꍇ�ł����Ă��A���ꂼ��̐l�����قȂ�����������Ă���A(3) ���͎҂𑪒�g�p�Ƃ���ꍇ�ɂ�errors of
measurement (�e�X�g��@�⎿�⍀�ڂȂǂɂ��G���[) �����ƂȂ�A(4) �C��⎞�Ԃ⎾�a�ȂǁA��������Ă�������v���Ƃ͕ʂ̉e��
15.14 Estimates of the terms in the model
�����ۂɊϑ��ł���f�[�^��J�O���[�v�̏]���ϐ��ł���n�̊ϑ��l�ł���A���A��j��A��ij�͖��m�̃p�����[�^�ł���B�����̐����least-squares
criterion�ɂ���čs���A����l����^�A��j^�A��ij^�ŕ\�L�����B(^ �͋L���̏�ɕ\�L�����)
�����肳���p�����[�^�̍��v�̓[���ƂȂ�Ɖ��肳��Ă���
(��1 + ��2 + �c + ��j = 0)
����^ = X.�o�[
��j^ = Xj �o�[ - X.�o�[
��ij^ = Xij - Xj�o�[ denoted my eij
Xij =
��^ + ��j^ + ��ij^ �ɑ������Ɓ@�ˁ@�v�Z��15.11 (p. 389) �ƂȂ�B
15.15 Sum of squares
��F����ɂ����ĕ���ƕ��q�͋A���������x�������ꍇ�A���U�������p�����[�^��2�̓Ɨ��\���ϐ�
(independent estimator) �Ɖ��肳���B���̃Z�N�V�����ł�SStotal����̍\���f
(SSB��SSw) �ɕ�����邱�Ƃ������B
���v�Z��15.11�̗��ӂ���X.�o�[���Ђ��A��悵���肷�邱�Ƃɂ��A���ӂ��������悤�ɂ��邱�Ƃ��o���邻�̌��ʂ�15.12�Ɏ�����Ă���B�ŏI�I�ɂ�SStotal = ��n��j^2 + ����eij2 = SSB +
SSW�ƂȂ�ASStotal��SSB��SSw�ɕ�����邱�Ƃ��������B
15.16 Restatement of the null hypothesis in
terms of population means
���A������ (��1 + ��2 + �c
+ ��j = 0) �ɂ����āA��1 = X1�o�[ - X.�o�[�ł��邱�Ƃ���A
��1�̊��Ғl��E (��1^) = E (X1�o�[ - X.�o�[) = E (X1�o�[) - E (X.�o�[) = ��1 - �� = ��1
�ˁ@��W�c�̋A����������1 = ��2 = �c =��j
15.17 ���R�x
��Degrees of freedom between groups, vB = J - 1 (�O���[�v�̐����}�C�i�X1)
���S�ẴO���[�v�̎��R�x�𑫂���vW = (n1- 1) + (n2 - 1) + �c (nJ - 1) �ƂȂ�B
�܂�Adegrees of freedom within
groups, vW = n.- J
balanced design�̏ꍇ�ɂ� vW = J (n - 1) �ƂȂ�B
��total degrees of freedom, vtotal = n. - 1�ł���Bn ��������balanced design �̏ꍇ�ɂ� vtotal = Jn - 1
15.18 Mean Squares: The expected value of MSW
�����R�x�Ŋ���ꂽSS��mean square (MS)�A��������variance estimate�ƌĂ�
��one-way ANOVA�ł�mean square
between (MSB = SSB / vB) ��mean square within (MSW = SSW / vW)�̓���d�v�ł���B���������x���J��Ԃ����ꍇ�A���Ғl�� E (MSB) �� E (MSW) �Ŏ������B
��J�̕�W�c���������U��2�����̂ł����MSW�̊��Ғl����2�ł��� (�v�Z��15.18, p. 394)�B
��MSW�͕�W�cJ�̕��ϒl����Ɨ����Ă��� (mean free�ł���)�B�e�O���[�v��������W�c���璊�o���ꂽ�ꍇ�ł����Ă��A�e�O���[�v���قȂ镽�ϒl�����ꍇ�ł����Ă��AMSW�̊��Ғl����2�ł���B
15.19 The expected value of MSB
��MSW�ƈقȂ�AMSB�͕�W�cJ�̕��ϒl�ɉe������B�S�ẴO���[�v�̕��ϒl���������A�����������藧�̂ł���AMSB�̊��Ғl����2�ƂȂ�B�������A�A�����������藧���Ȃ��ꍇ�AE (MSB) =��2
+ n����2
���A�����������p�����ꍇ�AE (MSB) > E (MSW) = ��2�ƂȂ�B��MSB�AMSW����Z�o�����F�l��p���āA�ǂ̂悤��type-I error�����ɋA�����������p�����̂��ɂ��ẮAsection 15.25���Q��
�y�[�W�g�b�v�ɖ߂�
2008/02/29
15.20
Some distribution theory (p. 395-98)
��16�͂ł́A���R�x�P�̃J�C����̕��U���݂邪�A���ŕ\���ƈȉ��̂Ƃ���F
�@(X-��)
2/��2 = z2�`��12
X������l�C�ʁ����K���z�����ϗʂ̕��ρC��2�����U
X�`NID (��,��2)�wij�͓Ɨ������ϗʂŁA���K���z���Ă��邱�Ƃ�\���B
��n�̓��_������ׂɒ��o���ꂽ�Ƃ��A�����̕��U�͈ȉ��̂悤�ɂȂ�B
�@(X1-��)2/��2+(X2-��)2/��2+...+(Xn-��)2/��2�`��n2
��n��z���_�ɂ�鑍�a�́A���R�xn�̃�2�l�̓�n2�ŕ\����Av = n�ɂȂ�B
X1����Xn�܂Ő��K���z�̓Ɨ���������l�ł���Ap.396�O�����̎��ɂ���ĂR�ʂ�ŕ\����B
��J = 3, n = 10�̂Ƃ��A�����a�͈͂ȉ��̂Ƃ���\�킵�A��2�l�̎��R�x��9�ƂȂ�B
�@SSw = ��(Xi1-�|X�ް1)^2 +��(Xi2-�|X�ް2)^2 +��(Xi3-�|X�ް3)^2
���܂��A�R�O���[�v���疳��ׂ�10���̓��_�𒊏o�����ꍇ�A���R�x�̓�9+9+92
�@�܂��272�ŁA�ȉ��̂悤�ɕ\�킳���B
�@SSw/��2�`��272
�������aSSw�UVw�Ŋ������Ƃ��̕��ϕ���MSw��
SSw/ Vw/��2�`��vw2/ Vw �܂��� MSw/��2�`��272/ 27
�����肩�����̂���ϗʂ���n�̓��_��ג��o����ꍇ�A
���K���z���Ă���̂ł���AX�ް�`NID (��,��2/ n)�ŕ\�킳��A���z�� (X�ް-��)
/���2/ n�ł݂邱�Ƃ��ł���B
���̂Ƃ����ς�0�ł���A���U��1�ƂȂ�B���ʂƂ��āA���R�x��1�̃�2�l��(X�ް-��)2/��2/ n = n (X�ް-��)2/��2�`��12
�������A�����������p�ł��Ȃ��i�L�ӂłȂ��j�ꍇ�́A
�@��n (X�ްj-X�ް�D)2 /��2�`��J-12
������ E (X�ް1) = E (X�ް)
= E (X�ް3) = E (X�ްj)
=�������藧���A��W�c�͓���̕��σʂ��������ϑ��ϗʂ̕��� X�ްj���璊�o���ꂽ�W�{�ł��邱�Ƃ������i��n��10��,�ϗʂ͂R�j�B
���ϗʂ̐�(J)�������邱�ƂŁA�ȉ��̓����Ń�2�l�͐����B
�@��10 (X�ްj-X�ް�D)2 / 2��2= MSB /��2�`��22/ 2
���A���������^�ł���i�L�ӂł͂Ȃ��j�ꍇ�A16. 6 (Section 16.5���Q�Ƃ̂���)�̓�������A�Ɨ������Q�̕ϗʂ��ꂼ������R�x�Ŋ��邱�Ƃɂ��AF���z�������B
[{��10 (X�ްj-X�ް�D)2 / 2��2 } /����(X�ްij-X�ްj)2] / 27��2�`F2, 27
�������ł̋A�������ł́A�ϐ�1, 2... J�ɂ͓��v�I�ȈႢ�͂Ȃ����Ƃ������Ă���B
�@SSB/ VB/ SSW/ VW�`FVB, Vw �܂���MSB/ MSW�`FVB, Vw
15. 21 The F-test of the null
Hypothesis: Rationale and Procedure (p.398)
�����U���͂̂��߂̕��z���_���������ƁF
�E���K���z�����W�c���疳��ׂɒ��o���ꂽ�R�̃T���v���Q������B
�EF�l�� F = MSB / MSW�ŋ��߂���B
�E��̌������ɌJ��Ԃ����ꍇ�AFig. 15.4�̂悤��F���z�������Ȑ����`�����B
�EF�䂪5%����ՊE�l���v�Z����ƁAF�l��3.36�̂Ƃ�
�����ɁA�T���v���Q�̕��ς��������Ȃ� (��1����2����3)�Ƃ��A�T���v����F���z��non-central�̔䗦����葽�����߂Ă���A�A�����������p�����B
�����������p�����Ƃ́AF���z����������E���ֈړ����Ă���AF�䂪�傫�����ڂ��Ă��邱�Ƃ�\�킷�B��ł� F2, 27�̂Ƃ�3.37�łQ�̋Ȑ���F���z����Acentral��non-central�łǂ���̔䗦�����������ׂ�B
���䗦�̍��������Acentral�Ȃ�A���������̗p�^non-central�Ȃ�A�������͊��p�B
��F���z�\�́A�����̕t�^�ɂ��Ă���A���ꂼ��5%, 1%�����ł̗ՊE�l���Q�Ƃł���B
�E�Q�Ƃ��ׂ�F���z�́A���R�x�ɂ���Ď�����镪�q�ƕ���i��F2, 27�j�ɂ���đΉ������Ċm�F����B
�� .95F2, 26= 3.37�i�T���v�������P������ƁA�ՊE�l�������ɏオ��j
����Ɠ����T���v�����o�@�i�R�Q����X�����j�Ŏ����������Ȃ��A����ꂽF���z��6.51���Ƃ�����H
�E.95F2, 27= 3.37�F�A�������̂Ƃ���̌��ʂ�100��̂���5��ɖ����Ȃ����Ƃ������B
�E.99F2, 27= 5.53�F�A�������̂Ƃ���̌��ʂ�100��̂���1��ɂ������Ȃ����Ƃ������B
������ꂽ6.51�Ƃ���F�l����́A�ɂ߂č��������݂ŋA���������^�ł͂Ȃ����Ƃ�������B
���A�����������p���邩�ۂ��̗ՊE�l��95%�Ƃ��邱�Ƃ͜��ӓI�ł�����A�ꍇ�ɂ���Ă�90%, 99%,�������� 99.9%�Ő��������邱�Ƃ��N���肤��B
�E�������A����50%��ՊE�l�ƒ�߂��Ƃ���A�����œ���ꂽ���ʂ���I���˂����_�Ɠ����ɁA��������_�������x�ɓ������ƂɂȂ�B
15.22
Type-I versus Type-II errors:��and��
�����Ƃ�����ꂽF���z�������Ă��A��ΓI�ɋA�����������p�ł���Ƃ͌���Ȃ��B
���A�����������p�����ꍇ�A�Η��������������Ȃ��\�����ǂ̂��炢�܂߂Ă���̂����ӂ��ׂ��ł���B
�E.95F2, 27= 3.37�����l�ƒ�߂��ꍇ�A5%�̌������z�������ʉ��߂��������B
�E����� .99F2, 27= 5.53�܂ŋA��������^�Ƃ���̂ł���A��������_���̑�����댯��1%�̊m���܂ŗ}����B
���ȉ���Fig. 15.5�Ɏ����悤�ɁA���߂̌��ɂ͓��ނ������āA���̊m�����傫��������A���������邱�Ƃ������Ƃ����B
�E�ꍇ�ɂ���Ă͗ՊE�l�𑀍삷��i���������Ȃ������ł́A���10%�ȏ�ɐݒ肷�邱�Ƃ����肤��j�B
������̌��́A���̊m�����T���v�������ɉe�����āA�����Ɣ�����A�����������p�ł��Ȃ��ꍇ�̂��ƁB���̂Ƃ�1-���͓��v�̌����
(power)�������A�m���߂�K�v������B
�E����͂����������Ƃ������ɍl�����A�����v�����Ŕ��ɏd�v�Ȗ��ł���B
�������R�X�g�i�T���v�����O�A�����ɂ����鎞�ԁj��₦�A�{���̌��ʂ�������邩������Ȃ��B
Fig.
15.5
|
H0 �͐^�ł��� |
H0 �͎����ɔ����� |
| H0 ���p |
�A���������^�ł���̂ɁA���p����
�i����̌��j |
�A�����������p���A����Ɍ��͂Ȃ�
�i�L�Ӑ�������j |
| H0 �̑� |
�A�������͐^�ł���A����Ɍ��͂Ȃ�
�i�L�Ӑ����Ȃ��j |
�A�����������p���ׂ��Ȃ̂ɁA�̑�����
�i����̌��j |
�����l��.05�Ƃ����ꍇ�A1-���ł̊��Z�l��.20�C����Ń��l��.10�ɂ����ꍇ�́A���Z�l��.50�ƂȂ��Ă��܂��B
�E����̌���Ƃ��댯��}���������A�ǎ��I�Ȍ��ʉ��߂Ƃ�����B
�����ʂ̂Ȃ����u���A���ʓI�Ɗ��߂Ă��܂����Ƃ������B
�������ړI�ɂ�邪�A���p�����ł͑���̌��������N���������[���ȏꍇ������B
��������ʓI�ȏ��u��A���Q�ƍl������v�����A���߂����Ă���댯������B
Fig.
15.6 �@������1-���̔䗦�������Ă���B
���.05����.01�Ɉ��������邱�ƂŁA����͂�������B
15.23
A summary of procedures for one-factor ANOVA (p. 402)
��J�ŕ\�킳���O���[�v�Ԃ̕��ϔ�r�������Ȃ��B���ꂼ���n�̓Ɨ���������l���܂܂�Ă���B
�E���`���f���ł͎��̂悤�Ȑ������@���O��ɂ���F
�@�P�D����
�@�@�A������(H0)�F��1 =��2 = ... =��j (H0�F��1 =��2 = ... =��j)
�@�@������(H1)�F��j��j2��0
(��ׂĂ���ϗʂ̕��ς͓����ł͂Ȃ�)
�@�Q�D�O��
�@�@�@��ij�`NID (0,����2)�ϗʂ͓Ɨ��A�����K���z���Ă��邱��
�@�R�D���蓝�v��
�@�@�@F = MSB / MSW
�@�S�D�W�{���o�̋敪
�@�@�@�A���������^�ł���Ȃ�AF���z�͋K��̎��R�x���������� (central) F���z���Ƃ�B
�@�T�D�ՊE�l�F 1-��FVBVW
�@�@�@F�l�����Œ�߂����荂����A�A�������͊��p����A�L�ӂƔ��f�����B
15.24
Consequences of failure to meet the ANOVA assumptions: The �grobustness�h of
ANOVA
���ꐔ���ʃ��f���ɗR�����邽�߁AANOVA�̕ϗʂ͓Ɨ����āA���K���z���Ă��邱�Ƃ��O��ɂ���B
�E���`���f���Ƃ́A�R�v�f����Ȃ�P���ȑ��a (Xij =��+��j+��ij)���瑪�肳���B
�@�@��:�l�̏㏸���ʏ�Ƃ���鑪��@
�@�@ j:������v������̌��ʁE�e��
�@�@��:�l���⑪��덷�A���̑�
�@�����Ƃ��ΐ��k�X�̗��K���ʂɂ��ω����l������ꍇ�A�Q�v���ŕ��͂�p����ׂ��B
��ANOVA�ł̂R�̑O��ɔ�����ꍇ�F
�@�i�P�j�ϗʂ����K���z���Ă��Ȃ��B
�@�i�Q�j�O���[�v�Ԃœ����U���Ă��Ȃ��B
�@�i�R�j�ϗʂ��Ɨ����Ă��Ȃ��B
���O��ɔ������ꍇ
�E�����̌����ŁA���ʓI�ȑO��̒E������Ă��邪�A�����Ȏ葱���Ő��m�Ȍ��ʂ���Ă��邱�ƂŌ����̊挒����������Ă���B
�E�ȉ��̑[�u���Ƃ�B
�@�P�D�̑������A����������A���ۂɎg����F�l�̗ՊE�_�����߂�B
�@�Q�D�ϗʂ̓����U����K���������Ă���Ƃ��́A���ۂɋ��߂�F���z�̗L�ӊm�������B
�@�R�D�v�悳��Ă����L�Ӑ����Ǝ��ۂ̗L�ӊm�����ׂ��Ƃ��A���܂�ς�肪�Ȃ��Ƃ���̂ł���A�葱�����挒�ł���Əq�ׂ�B
�� t����ł̐��K���E�����U���̑O��ɑ���挒���́AANOVA�ɂ���ʉ��ł��邱�Ƃ��m�F����Ă���B
�EGlass, Peckham, & Sanders
(1972)�ɂ��O������ĂȂ�ANOVA�ł̌��B
�P�D���K���z���ĂȂ����Ƃɂ�����E����̌����\���͋ɂ߂ĒႢ�B
�i�������T���v���̘c�x�������A�ϑ��������Ȃ��A�Б�����ł����Ȃ��ꍇ�������j
�Q�D���������œ����U���Ă��Ȃ��Ă��A����̌�������A����͂Ȃ��\���͏��Ȃ��B
�@��r�O���[�v�������A�����Ή����Ă���ꍇ�A�ʏ���T���߂Ȍ��ʂ��o��B
�@�����傫���A��r�O���[�v�����Ȃ��ꍇ�A�L�Ӑ����Â�(?)�ɏo��B
�@�����U��������t�����Welch�@������悤�ɁA�s�ލ����ȕϗʓ��m�̔�r�Ɏg����ANOVA������(Sec. 15.25)�B
�R�D�ϗʂ̓Ɨ����͐��m�ȗL�ӊm�������߂�̂ɕK�v�B�ϗʂ��Ɨ����Ă���Ƃ������Ƃ́A��ׂĂ���ϗʂ��݂��ɉe�����Ă��Ȃ����Ƃ����A�w���@�̒����Ńf�B�X�J�b�V������O���[�v�E�J�E���Z�����O�Ȃǂ������Ȃ��ƁA�ϗʂ̓Ɨ����ɂ��e������B�Ɨ������������ϗʂ��r����ƁA����̌����N�����₷���Ȃ�B
15.25
The Welch and Brown-Forsythe modifications of ANOVA: What
does one do when��2�fs and n�fs differ?
��15.20�̌����ɂ���Ƃ���AWelch�̖@�����p����A�ꕪ�U���������Ȃ��ϗʂR�ȏ�ł�ANOVA��p���邱�Ƃ��ł���B
�EF�l�̗ՊE�_�́A
�@���ꂪ�O���[�v�̐�����P�� (J-1),
�@���q�� 1/VW = [3 / (J2-1)]��j [(1-wj/ u)2 / (nj-1)]�ŋ��߁AF���z�\ ((?) Table F)���Q�Ƃ��邱�Ƃŕ�����B
�E�ǂ��炩�Ƃ����ABrown-Forsythe�̏C����������������(15.21)�B
�@���O���[�v�����Q�̏ꍇ�AWelch��t�l��Brown-Forsythe��F*�l�͓������Ȃ�B
15.26
The power of the F-test
���s���Ȋw�A�Љ�Ȋw����̒����ł͏[���Ȍ���͂�����ꂸ�A�{���͈Ⴄ�͂��̌��ۂ��ł��Ȃ����Ƃ�����B
�E���������������Ȃ��ȑO�ɁA����͂̂��߂̌��ʗʂ�\�����邱�Ƃ�W���I�Ȏ葱���ɂ��ׂ��B
���v���ЂƂ�ANOVA��F�l�ɂ�錟��̌����(1-��)�́A�ȉ��̂Ƃ���̎葱���ށF
�P�D���ς̈Ⴂ�̑傫����\�킷�̂ɁA�d�݂Â���ꂽ�e��nj��j2�ɂ���đ����Ă���B
�@�����Ŏ�����j�Ƃ́A��ׂ�ׂ��ϗ�j�ɑ��鑍���ς̍��̂���
(��j-��)�B
�Q�D�ϗ�X�̕��σʂƌ��ʃ�j�ő���s�\�Ȍ덷�ϗʂ́A�v���ЂƂ̂Ƃ���W2 =����2
�R�D���R�x�̕��q�̓O���[�v����P�������� (vB = J-1)
�S�D���R�x�̕���́A�v���ЂƂł���Α�������v���̐��ň������l(vW = n.-J)
�T�D����̌����\���̓��Ŏ����B
������͂𐔒l�����邽��15.22�̎���non-centrality
parameter (?)�����肷��i�ӂŕ\�L�j�B
�@����n���ύt�����ꂽ�f�U�C���ł���A�P��������15.23�̌������g����B
�@���ϗʂ̐���2�ł���A�ӂ͌��ʗʇ��ƌ����狁�߂���(15.24�̎�)�B
15.27
An illustration
����������f�U�C���ŁA40�����̃O���[�v�Ńe�X�g���_����(��)���A�����Q= 90�CGroup
2 = 95, Group 3 = 100�̂Ƃ�����͂����߂�ƁA
�E�e�O���[�v�̌��͓����Ȃ̂ŁA15.23�̌����ɒl��������=
1.72
�E���͂��̂܂܂ŃO���[�v���Q�̏ꍇ�A����͂���= 2.11
���ӂ���[���߂���A�t�^��Table G����1%�^5%�����ł̌���͂��Q�Ƃł���悤�ɂȂ�iTable�̎g�����͈ȉ��̂Ƃ���j�B
�P�DvB�ɉ����āA�Y����figure���݂���B
�Q�D���l�̊��5%�܂���1%�̂����ꂩ�I�ԁB
�R�Dp.407�̎�����ӂ����߂�B
�S�D����l�̑�������O���[�v�̐����������l(n.-J)�����߁A�^�e���ɍ��킹��B�����āA�P.��figure�ƂŌ�_���݂���B
�T�D��ł́A��= 1.72, Ve = 117�̋Ȑ����Q�Ƃ��A(1-��)�̌���ׂ͂�Ƒ��
.65�Ō������Ă���B���̌��ʂ���́A����̌��������N�����\���������B
15.28
Power when��is unknown
�������̌����ŁA����ɂ��Ђ����O�ɋ��߂��Ȃ����Ƃ�����B���̏ꍇ�A�W�����ł̕��ύ����l���ɓ���邱�Ƃ��ł���B
����D�����Qgroup 1���ł��Ⴍmean��0�Ƃ����ꍇ�A�ł����ʓI�ƌ����܂��group 3��1SD�E�ɁAgroup
2�͗��Q�̐^��0.5SD�E�ɂ���ĕ��z���� (Fig. 15.7)�B
�E�O���[�v�Ԃ̌����قȂ�An1��n3��20�An2��40�Ƃ����ꍇ�A15.22�̎��֑�����A��=
1.83�Ƌ��߂���B
�ETable G����A���q2,����77�i���悻�̒l80���Q�Ɓj��
1%�����ł� .57�̌����݁B
15.29
A Table for estimating power when J = 2
������͂̂��߂̌��ʗ�(1-��)����ɏ������ꍇ��(.1��)����傫���ꍇ��(1��)�Ŏ����ƁA��r����O���[�v(J)���Q�O���[�v�ł���ATable 15.4�Ŏ����悤�ɂȂ�B
�@���T���v���T�C�Y�ɉ����āA����͍͂��܂�B
15.30
The non-parametric alternative: The Kruskal-Wallis test
���N���X�J���E�E�H���X�̌���ł̓T���v�����O�E�G���[�ɂ�錋�ʂ̈Ⴂ����r�ł���B
�@���T���v���̐��K�������肳��Ȃ��Ƃ��ɗp����B
�EANOVA�ŕ��͂����Ƃ��A�ϐ��Ԃ̌�n�ɂ��܂�ɂ��Ⴂ�����肷����Ƃ��B
�E�N���X�J���E�E�H���X�̌���͏����one-way ANOVA�悤�Ȕ�r�������Ȃ��B
�@�����́A�Q�̌��茋�ʂő傫�ȕω��͂Ȃ��B
��Welch�@��Brown-Forsythe���g���A����͂̍�����ANOVA���̂̊挒������A�N���X�J���E�E�H���X�̌���͋ɒ[�ɊO��l���o�Ȃ�����A�قƂ�Ǘp�����Ă��Ȃ��B
���ق��ɂ��A���z�̒����t�߂ł̈Ⴂ���m���߂���̂ɁA�Ԏ��撆���l���肪���邪�A�N���X�J���E�E�H���X�̌���قǂɂ͌���͂������Ȃ��B
�f�B�X�J�b�V�������R�����g
�E�@Fig. 15.5�Ɋւ��āA���́A��P��̌���Ƃ��m���̂��ƂŁA�����̗��Ă������iH1�j���������Ȃ��̂ɁA�������ƌ��_�t���Ă��܂��m���B���́A��2��̌���Ƃ��m���̂��ƂŁA�������������̂Ɂi�A�����������p�����ׂ��Ȃ̂Ɂj�A�������Ȃ��Ƃ������Ƃ��m���̂��ƁB
�E�@�ێ�I�ɂȂ肷���āA���̑�2��̌��iType II error�j�̕����[���ȏꍇ������̂ŁA���̌���Ƃ��Ȃ��m���i����́F�P�|���j�ׂĂ݂邱�Ƃ���B�Ⴆ�A����͂�.80�Ƃł�A100�̉�������100�āA80��͂��̎�̌���Ƃ��Ȃ��Ō��o�ł��邱�Ƃ��Ӗ�����B���̌���͂́A�T���v�����𑝂₷�Əオ��̂ŁA�ǂꂮ�炢�T���v�����𑝂₷�ׂ������������邱�Ƃ��ł���B
�E�@�ǂ���̌����Ƃ��Ȃ��悤�Ɍ��_�����߂ɂ́A�L�Ӑ����isignificance criterion�j,���o�́ipower�j�A���ʗ� (effect size)�A�W�{�� (sample size)��4�̃p�����[�^�iCohen, 1988�j���l�����Ĕ��f���邱�Ƃ��]�܂����B
�E�@�t�^��Table G�ipower�F�P�|���j�̓ǂݕ�����������B�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i����A�C�j
�y�[�W�g�b�v�ɖ߂�
2008/03/14
Chapter 16 Inferences about variances
���ǂݑւ����@�搔�̍��ׂɂ� ^ ���C�L���̉E�Ɍ���鉺�t�������̍��ׂɂ�
# ��\�L������B
16.1 Introduction
���@�����҂͕��ς⊄���⑊�W���ɋ��������邱�Ƃ��������Aquestions of variability�i�ϗe���j�ɋ��������邱�Ƃ�����B������J�C��敪�z�Ō��Ă݂�B
�i��j�j�q�̕������w�̏n�B�x�e�X�g�ɂ�����l�������q�����傫��
16.2 Chi-square distributions
���@��W�c�����K���z���Ă��ĕW�������ꂽz-score�����W�c���Ɖ��肵�Ă݂�B���̕W�������ꂽ�l����悳��iz#i ^2�j�A��#i ^2�� (?) �����_���ɑI�ꂽ�Ƃ���B���̂Ƃ��A��#i ^2 = z#i ^2�ɂȂ�B������قږ����ɌJ��Ԃ����Ƃ��̃O���t��p. 423��Figure 16.1�ł���i���R�x��1�j�B
���@z���z��t���z�Ɠ��l�ɁA�J�[�u�̉��̕��������v�����1�ɂȂ�B��#i ^2��1���傫���̂�32%���ł���B�t�Ɍ����ƁA�p�[�Z���^�C�����ʂ�68�ʂ̏ꍇ�A��#i ^2��1�ɂȂ�B�p�[�Z���^�C�����ʂ�95�ʂɂȂ�̂̓�#i ^2��3.84�̂Ƃ��ɂȂ�B
16.3 Chi-square distributions with �� > 1: ��#2 ^2 and ��#3 ^2
���@���R�x��2�̂Ƃ��Ƃ����̂́A1��z���_��I�Ԃ̂łȂ��A2�̓��_�����̐��K���z����z���_���烉���_���Ɏ��o���Ƃ��ł���i��#2 ^2 = z#1 ^2+ z#3 ^2�j���ꂪ���x���J��Ԃ�����p. 424��Figure 16.2�̂悤�ȃO���t�ɂȂ�B
16.4 The chi-square distribution with �� degrees of freedom, ��#�� ^2
���@���R�x���˂̂Ƃ��́A�ˌ�z���_�̓��𑫂������̂���^2�̒l�ɂȂ�B�J�C��敪�z�͎��R�x�ɂ���Č`���قȂ�iFigure 16.3�j�B�J�C��敪�z�̓����͈ȉ��̒ʂ�B
(a) ���R�x���˂̂Ƃ��̃J�C��敪�z�̕��ς̓˂ɂȂ�B�Ⴆ�A���R�x��12�̂Ƃ��̃J�C��敪�z�̕��ς�12�B
(b) ���R�x���˂̂Ƃ��̃J�C��敪�z�̍ŕp�l�́A�˂�2�ȏ�ł����-2�̒l�B
(c) ���R�x���˂̂Ƃ��̃J�C��敪�z�̒����l�́A�˂�2�ȏ�ł���Α�� (3��-2)/3 �B
(d) ���R�x���˂̂Ƃ��̃J�C��敪�z�̕��U��2�ˁB
(e) ���R�x���˂̂Ƃ��̃J�C��敪�z�̘c�x�́�2/v�B�J�C��敪�z�͑S��positively skewed�����A���R�x���オ��ɂ�č��E�Ώ̂ɋ߂��Ȃ�B
(f) ���R�x���ƂĂ��傫���Ȃ�ƁA�J�C��敪�z�͐��K���z�ɋ߂Â��i���ς��˂�SD����2�ˁj
16.5 Inferences about the population variance: H#0 = ��^2 = K
(a) �������A�������́A��W�c�̕��U��K�Ɠ����ł���Ƃ������ƁB
(b) �O��́A�ϐ�X�����K���z�����Ă��ă����_����n�����o����Ă���Ƃ������ƁB
(c) �A�������������鎮�͎�16.4�̒ʂ�B
(d) �A���������̑������A�T���v���̕��z�̓J�C��敪�z�Ɠ����ł��邱�ƂɂȂ�B
(e) ���p��̓�/2��1- (��/2)�̃p�[�Z���^�C�����ʁB
(f) 1-���̐M����Ԃ͎�16.5�̒ʂ�B
16.6 F-distributions
���@2�̂��̂̕��U���قȂ邩�ǂ����ׂ�Ƃ��ɁAF���z��m���Ă������Ƃ͗L���ł���i�Ȃ��Ȃ�A��������H#0 : ��#1 ^2 = ��#2 ^2 ������B�j�B
���@���R�x��10�̂Ƃ��Ǝ��R�x��5�̂Ƃ����l���Ă݂�i��F���R�x��5�̂Ƃ��A�J�C���l�̓����_���ɂƂ���5�̓Ɨ������l�̓��̑��v�j�B����2�̃J�C���̒l�̔��F��ɂȂ�i��16.6�̒ʂ�j�B
16.7 Inferences about two independent variances: H#0 :��#1 ^2 = ��#2 ^2
(a) ��̕��U�������ł���Ƃ���������������ق����A��W�c������l�Ɠ������U�����A�Ƃ��������̌�������ʓI�ł���B2�̕��U�������ł���Ƃ����A�����������������Ƃ���B
(b) n#1 �̃T���v���������_���Ɏ��o����Ă����Ƃ���B�܂��An#2 �̃T���v�������o����Ă����Ƃ���B���ꂼ��̃T���v���̕�W�c�̕��ϒl�́A�A�������Ƃ͖��W�ł���B
(c) �����������ɂ�F���p����B
(d) �A���������̑������Ƃ��AF�l�̓�#1 = n#1 -1�ƃ�#2 = n#2 -1��F���z�ł���B
�Η��������̑������Ƃ��As#1 ^2/s#2 ^2�̓�#1 ^2/��#2 ^2�ƃ�#1 = n#1 -1�ƃ�#2
= n#2 -1��F���z�����������̂ł���B
(e) ���p���p. 430�̎��Ɏ������Ƃ���B
(f) �M����Ԃ͎�16.9�Ɏ������Ƃ���B
16.8 Testing homogeneity of variance: Hartley's F#max test
���@�����U����������e�X�g�͊������BHartley's F#max test�͂ƂĂ��ȒP�ł���i�A���O���[�v�Ԃ̃T���v���T�C�Y�������Ƃ��Ɏg�p����j�B�A�������́A���ꂼ��̃O���[�v�̕�W�c�̕��U�͓������A�Ƃ������̂ł���B
���@F#max = s^2#largest / s^2#smallest �ł���AAppendix��Table H�Ɋ��p�悪�f�ڂ���Ă���B�O���[�v��3�ȏ�̎��ɂ́A�M����Ԃ͂��܂�Ӗ����Ȃ��B
16.9 Testing homogeneity of variance from J independent samples: The Bartlett test
���@Bartlett�̌���̓��O���g���K�v������BBartlett�̌���́A�O���[�v�ԂŐl�����قȂ�ꍇ�ł��g�p�ł���B
���@�A�������͂��ꂼ��̃O���[�v�̕�W�c�̕��U�͓������A�Ƃ������̂ł���B�J�C��挟���p���Č�����s���ip. 434��16.11���j�B�O���[�v��3�ȏ�̎��ɂ͐M����Ԃ͂��܂�Ӗ����Ȃ��B
16.10 Other tests of homogeneity of variance: The Levene and Brown-Forsythe tests
���@Levene�̌����ANOVA�Ɠ��l�ŁA�ϑ��l�����ς���ǂꂭ�炢����Ă��邩�Ƃ������Ƃł���BLevene�̃e�X�g�͐��K���z�̑O��Ɋ挒���ƍl�����Ă������߂悭�g�p����Ă������A���ۂ͊挒�ł͂Ȃ��BLevene�̌���́A�f�U�C����balanced�ȂƂ��݂̂ɐ��m�ɂȂ�B
���@���l�̂��̂�Brown & Forsythe���m���������̂�����B�����Levene�̌���Ɠ��l�����A���ς̑���ɒ����l����̈�E��p����B��W�c����x��c�x�̓_�Ő��K���z�����E���Ă��Ă��A���m�Ȓl���Z�o�ł��邱�Ƃ�������Ă���B
���@�������A�T���v�������O���[�v�ԂňقȂ�ƁALevene�̃e�X�g�Ɠ��l�̖�肪�N����i�B���̂悤�ȂƂ��ɂ́A�O���[�v����2�̏ꍇ�ɂ�Welch t'��p���A�O���[�v����2�ȏ�̏ꍇ�ɂ�Welch F'��Brown-Forsythe F*��p����Ƃ����B�T���v�������O���[�v�Ԃł��܂�ς��Ȃ��Ƃ��ɂ́A�T���v�������������Ȃ�܂Ń����_���ɃT���v�����Ă����āABrown-Forsythe test���s���Ɨǂ��B�c�x�����ł����Brown-Forsythe��p���A���z�����K���z���炠�܂��E���Ă��Ȃ��悤�ł���ABartlett�̌����p����̂��ǂ��ł��낤�B
��SPSS�ł�Levene���f�t�H���g�Ō����Ǝv�����ABrown-Forsythe���o����̂��낤���H
16.11 Inferences about H#0 :��#1 ^2 = ��#2 ^2 with paired observations
���@�A��������H#0 :��#1 ^2 = ��#2 ^2 �ł���B���K���z�ł��邱�Ƃ��O��B����̎���p. 437��16.12���B
16.12 Relationships among the normal t, ��^2, and F-distributions
���@t���z, ��^2���z, F���z�͐��K���z�ɗR�����Ă���B
���@���R�x��������̍ۂ�t���z�͐��K���z�ł���Bt�̓�悪F�ɂȂ�it��F���������R�x�̂Ƃ��j�B�܂��AF���z�ƃ�^2�̊W�́A��^2�����R�x�Ŋ��������̂�F�ɂȂ�Ƃ������̂ł���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�X�{�j
�f�B�X�J�b�V�������R�����g
�ELevene�̌���ȂǁA���K���ɑ��Ċ挒�ł���Ǝv���Ă��錟��@�ł��A����̂悤�ɂ����ł͂Ȃ����Ƃ�����̂ŁA���R�̂��Ƃł͂��邪�A������s���O�ɂ�������Ɛ��K�����ᖡ�������B
�E�O���[�v��3�ȏ�̎��̐M����Ԃɂ͂Ȃ��Ӗ��������̂��ɂ��Čl�I�ɂ͋���������B�@�@�@�@�@�@�@�@�i����j
�y�[�W�g�b�v�ɖ߂�
2008/04/07
Chapter 17 Multiple Comparisons and Trend Analysis
<�ǂݑւ����@�搔�̍��ׂɂ� ^ ���C�L���̉E�Ɍ���鉺�t�������̍��ׂɂ�#
��\�L������B
17.1 Introduction
���@F�����J�S�ẴO���[�v�̕��ς��������A�Ƃ��������̌��ł���BJ��3�ȏ�̏ꍇ�ɋA�����������p���ꂽ�ꍇ�́A�u�S�Ă�J�̕�W�c�̕��ς��������킯�ł͂Ȃ��v�Ƃ������ƂɂȂ邽�߁A�S�ẴO���[�v�ԂŗL�Ӎ�������ƌ����킯�ł͂Ȃ��B���̂悤�ȏꍇ�ɑ��d��r���p������B
���@���d��r���p������悤�ɂȂ�O��t���肪�p�����Ă����B�������At����͂����̃O���[�v�����邩���l�����Ă��Ȃ��B�O���[�v����3�ȏ�̏ꍇ�AType I error��.05�����傫���Ȃ�B
���@���d��r�ɂ͂��낢��Ȏ�ނ����邪�A���̏͂ł͂悭�g�p�����7���Љ��B
17.2 Testing all pairs of means: The studentized range statistic, q
���@���d��r��p����T�^�I�ȏ́A���ꂼ��̕��ϒl�𑼂̑S�Ă̕��ϒl�Ɣ�r�������ꍇ�ł���B���̃y�A�̐��́AC = J (J-1) /2�ɂȂ�i�O���[�v����12�̎��ɂ�66�y�A���o����j�B���̂悤�ȑS�Ẵy�A�ɂ����Ĕ�r����Ƃ��ɂ́Astudentized range statistic, q��p����B�������̑��d��r�̕��@�͂����p���Ă���Bt������J��Ԃ��̂Ƃ͈Ⴂ�Aq�̓O���[�v�����l���ɓ���Ă���B
���@q��2�̕��ϒl�̍����A���ς̕W���덷�Ŋ��������̂ł���iq�̊��p�l��Appendix��Table I�ɂ���j�B
17.3 The Tukey method of multiple comparisons
���@Tukey�̕��@�́A�܂��ł����ϒl���قȂ�y�A���r���邱�Ƃ���n�߂�BAppendix��Table I����A���ϒl�̐��A���R�x�A����ǂݎ��B�����ł����A�ł����ϒl���قȂ�y�A���L�ӂłȂ�������A���̑��̃y�A�̔�r�͕s�K�v�ł��낤�B�����L�ӂł���A2�Ԗڂɕ��ϒl�̍����傫���y�A�ɂ��čs���B
���@�T���v���T�C�Y�������ꍇ�ɂ́ATukey�̕��@�͎�v�Z�ł��\�ɂȂ�B����́A�A�����������p�ł���ŏ��̍���T�����Ƃɂ���čs���Ahonest significant difference (HSD)�ƌĂ��B
17.4 The effect size or mean differences
���@���ʗʂ�p. 449��17.6���ŋ��߂���B���ʗʂ͕��ϒl�Ԃ̍��̒��x��\�����̂ł���B
17.5 The basis for Type-I error rate: contrast versus family
���@���d��r�ł́AType-I error�����ꂼ��ɒ�߂邩�icontrast-based�j�A����Ƃ�1�̃��Ƃ��Ē�߂邩�ifamily-based�j�Ƃ����I��������B�{�͂ŏЉ��7�̑��d��r�̂����A5�̓���1�ɒ�߁A2�͌X�Ƀ����߂�B��قǏЉ��Tukey�́A1�Ƀ����߂���̂ł���B
���@����2�̂ǂ��炪�悢���ɂ��Ă͈ӌ���������Ă���B�X�Ƀ����߂��������͂��������AType-I error�̊댯���傫���Ȃ�B1�̃����߂�ƁAType-I error�͏��Ȃ��Ȃ邪�AType-II error���������₷���Ȃ�B���҂����́A�X�Ƀ����߂���𐄏����Ă���B
17.6 The Newman-Keuls method
���@Newman-Keuls (NK) method��Tukey�ƂƂĂ����Ă��邪�ANK method�͌X�Ƀ����߂Ă���B
���@�ŏ��̒i�K��Tukey�Ɠ����ŁA�ł����ϒl�̍����傫���y�A�ɂ��Ē��ׂ�B�����ŗL�Ӎ���������A�S�Ă̋A�������͎x�������B�����A�����������p�����A���̔�r���s����B���̍ۂ�q�̊��p�l�́Ar = J-1����ɍs����i�܂�O���[�v����1���炵�čs���悤�Ȍ`�ɂȂ�j�B�����ł��A�����������p�����AJ-2, J-3�Ƃ����悤�Ɍ��肪�������Ă����B
17.7 The Tukey and Newman-Keuls methods compared
���@Tukey��Newman-Keuls�̈Ⴂ�́A���̈Ⴂ�ł���B�ŏ��̒i�K�̌���ȊO�́ANK�̕�����茟��͂����i�ŏ��̒i�K�ł̌���͓͂������j�B
17.8 The definition of a contrast
���@contrast-based��family-based��type I error����ʂ��邽�߂ɁAcontrast�̒�`�Asimple contrast��complex contrast�̋�ʁA������planned��post-hoc contrast�̈Ӗ���m���Ă����K�v������Bcontrast�Ƃ�2��subset�̕��ϒl�́A���ς̍��ł���ithe mean difference between two subsets of means�j�BTukey��NK�@�̏ꍇ�ɂ͂��ꂼ���subset�ɕ��ς�1�����Ȃ���������Ȃ����A3�ȏ�̕��ς�����ꍇ������B
17.9 Simple versus complex contrast
���@2�̕��ϒl�̍���simple contrast�i��������pairwise contrast�j�ł���BJ = 2�̎��ɂ�contrast��1�݂̂����AJ = 3�̏ꍇ�ɂ�3��contrast������B�A�������́A�S�Ă�contrast��0�ł���A�Ƃ������̂ł���B���̋A��������t����ȂǂŒ��ׂ邱�Ƃ��ł���B
���@complex contrast��3�ȏ�̕��ϒl���܂ނ��̂ł���Bimplicit�ȋA�������́A�A�������́A��#3����#1�ƃ�#2�̕��ϒl�Ɠ������A�Ƃ������̂ł���B
17.10 The standard error of a contrast
���@����Ȍ㈵�����d��r��t ratio���g�p���錟��ł���B�܂�Acontrast�̐���l�Ɛ��肳�ꂽ�W���덷�̔�ł���Bcontrast�̕W���덷�͎�17.8�ŎZ�o�����B
17.11 The t-ration for a contrast
���@contrast��t ratio�́A���肳�ꂽcontrast�Ƃ��̕W���덷�̔�ł���Bt ratio�����v�I�ɗL�ӂ��ǂ����́A�g�p���鑽�d��r�̕��@�ɂ��B���d��r�́A���ꂼ��قȂ鐧���������߁A���p�l���قȂ�B���̍ہAplanned��post hoc���A�Ƃ�����r���d�v�ɂȂ�B
17.12 Planned versus post hoc comparisons
���@���d��r�̕��@�Ԃŋ�ʂ�����ۂɂ́Aplanned��post hoc���A�Ƃ����Δ䂪�d�v�ł���Bplanned�ł́A�f�[�^���W�߂�O�ɉ�����������Ȃ���Ȃ�Ȃ��B��r�I������subset�̍ۂɂ́Aplanned�̂ق���post hoc��������͂������Bplanned�̗��_�I�����́Aone-tailed t test�Ǝ��Ă���B
���@post hoc�̑��d��r�͓��ʂ�specification�Ȃǂ͕K�v�Ƃ��Ȃ��BTukey��NK�@��post hoc�ł���B
17.13 Dunn (Bonferroni) method of multiple comparisons
���@Dunn��t�̊��p�l���߂邽�߂�Bonferroni inequality���g�p�����i�S�̂̃��́A���ꂼ��̃��𑫂������̈ȉ��Ƃ������́j�B�Ⴆ�A�� = .01��5����s�����ꍇ�A����Type I error��.05�ȉ��ł���Ƃ������̂ł���B���̏ꍇ�Aplanned�̌���łȂ���Ȃ�Ȃ��B
���@���̕��@�͂ƂĂ�flexible�ŁAsimple, complex��contrast�������ł��g�p�ł���B
17.14 Dunnett method of multiple comparisons
���@Dunnett�̕��@�́A1�̕��ς�J-1�̕��ςƔ�r����Ƃ��p�̂��̂ł���B�]���āAJ-1�̃y�A������Ɖ��肵�Ă���i�����Q������ȊO�̎����Q�Ƃ��ꂼ���r����悤�ȏꍇ�j�BDunn��Dunnett������⌟��͂��Ⴂ�B
17.15 Scheffe method of multiple comparisons
���@Scheffe�͍ł��悭�g�p����鑽�d��r�@�ł���A�ƂĂ�flexible��post hoc�ȕ��@�ł���B�����family of contrast�ɑS�Ă�simple & complex contrast���܂߂���̂ł��邽�߁At�̊��p�l�����̑��d��r�@�����傫���i���ɃO���[�v���������ꍇ�j�B�O���[�v���������̂ł���ATukey��NK�@���ǂ��ł��낤�B
17.16 Planned orthogonal contrast
���@planned orthogonal contrast (POC) �́A���ϒl�̍��ɂ��Ă̍ł�����͂�����e�X�g�ł���B�T���v�����������O���[�v�̃f�U�C���ł���A2��contrast�́Acontrast coefficients�̑��v��0�̏ꍇ�ɂ͒������Ă���BPOC�ł́A�S�Ă�contrast���������Ă��邱�Ƃ������ƂȂ�B
17.17 Confidence intervals for contrast
���@Tukey�ł̐M����Ԃ�17.14���̂悤�ɕ\�����B�܂��A�l�X�ȑ��d��r�ł̐M����Ԃ̌��ʗʂ�Figure 17.1�Ŏ�����Ă���B
17.18 Relative power of multiple comparison techniques
���@���d��r�ł̗D�ʂɂȂ镽�ϒl�̍��́A���@�ɂ���ĈقȂ�B
(a) POC�͍ł��������l�ŗL�ӂɂȂ�
(b) NK��POC�́A�אڂ���ordered�ȕ��ςł���A�����l�ŗL�ӂɂȂ�
(c) Tukey��NK�̍ŏ��̔�r�͓����ł���
(d) planned�ł���ATukey��Dunn����⌟��͂�����
(e) Dunn��Dunnett���������p�l������
(f) Scheffe�͍ł��������p�l��K�v�Ƃ���
17.19 Trend analysis
���@trend analysis��planned orthogonal comparison�Ɨގ����Ă��邪�A�ʏ�͗v����J�̘A���������x�������肷��Ƃ��Ɏg�p�����i�N��A�w�N�AIQ�Ȃǁj�BTrend analysis�ł́A�Ɨ��ϐ�X��Y�̊Ԃɒ����́A�������͔��̊W������̂��ׂ邱�Ƃ��o����B�������ł���A�ł����Ă͂܂肪�ǂ���A�̐����������Ƃ��ł���iFigure 17.2�j�B
���@trend analysis�ł͑��֔�i��^2�j��p���ċȐ��I�ȉ�A����̐������ׂ邱�Ƃ��ł���ii.e. r^2�͒�������̉�A�̂݁j�B
17.20 Significance of trend components
���@p. 465��Table 17.5�ł́Aquadratic�̕����݂̂��L�ӂɂȂ��Ă���i������Ȃ�Ȃ̂��A�Ƃ������Ƃ܂ł͓ǂݎ��܂���ł����c�j
17.21 Relation of trends to correlation coefficients
���@������trend�ƃs�A�\���̑��W���ɂ͕��s�I�ȊW������B
17.22 Assumptions of MC methods
���@�{�͂ň������S�Ă̑��d��r�́At�����ANOVA�Ɠ����O����i���K���A�����U���A�Ɨ����j�B���d��r�͐��K���ɂ͊挒�����A�����U���ɂ��Ă͊挒�Ƃ͂����Ȃ��B�]���āA�T���v���T�C�Y���������ꍇ�ł������U���ɂ��Ă͊m�F���Ă������Ƃ��K�v�ł���B�����U������������Ȃ��ꍇ�ɂ́AWelch quasi-t'��Brown-Forsythe test���g�p�ł��邵�A�܂�Bonferroni�̏C�����s����B
17.23 Multiple comparisons among other statistics
���@Marascuilo (1966) ��large sample method�ɂ����āA��17.7������ʓI�Ȏ����`�����i��17.21�j�B
p. 470�ɁA�ǂ̑��d��r��p����悢���A�Ƃ����t���[�`���[�g���f�ڂ���Ă���
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�X�{�j
�f�B�X�J�b�V�������R�����g
�E���d��r�@�̎�ނɂ���ĕ��ϒl�̗L�Ӎ����ǂ̂悤�ɈقȂ�̂����w�Ԃ��Ƃ��o�������A���g�̌����̖ړI��f�U�C���A�f�[�^�ɉ����Ďg�������Ă����K�v�������߂Ċ������B
�E�l�I�ɂ�planned��post hoc�̎g�������ȂǁA�s���m�ȓ_�����������̂ŁA����̉ۑ�Ƃ������B
�y�[�W�g�b�v�ɖ߂�
2008/04/18
Chapter 18: Two- and Three-Factor ANOVA: An Introduction to Factorial Designs
Glass, G. V., & Hopkins, K. D., (1996). Statistical methods in education and psychology. Boston, MA: Allyn & Bacon.
<�ǂݑւ����@�搔�̍��ׂɂ� ^ ���C�L���̉E�Ɍ���鉺�t�������̍��ׂɂ�# ��\�L���Ă���B
18.1 Introduction
���z�u���U���͂Ō�����鉼����3��
1. Whether the J means of factor A are equal in the population
2. Whether the K means of factor B are equal in the population
3. Are there certain combinations of the two factors that produce different effects from what would be expected from the two factors considered separately?
��1�C2�͂��ꂼ��̗v����ʌɈ���main effect�ł���A�ꌳ�z�u���U���͂ɂ����鉼���Ɠ����B3�_�ڂ̉������z�u���U���͂ŏd�v�ƂȂ�v��A�Ɨv��B�́u���ݍ�p (interaction)�v�Ɋւ�����̂ł���B���̌��ݍ�p��2�̗v�����P�Ƃō�p����̂��A����Ƃ�2�̗v�������݂ɉe���������̂��������Ă���B
���z�u���U���͕͂����̗v��������multiple-factor ANOVA�ł͍ł��V���v���ȃf�U�C���ł���A�v���̐��������Ȃ�Ƃ�蕡�G�ȃf�U�C���ƂȂ�B
18.2 The meaning of interaction
��treatment�̉e���̗L���ɉ����A�ǂ̂悤�ȑΏۂɉe��������A�ǂ̂悤�ȑΏۂɂ͉e�����Ȃ��̂���������ۂɗp������ (e.g., Is the new method more effective for high- than for low-ability students?)�B�������ꂼ��̑Ώۂɑ���e���ɈႢ������ꍇ�ɂ�interaction������Ƃ�����B
Interaction examples
�E�قȂ鍑�Ђ̊w����test-wiseness��2��ނ̎���`���łǂ̂悤�ɈقȂ邩������
�E�P��w�K�ɂ����āA�Љ�o�ϓI�ɒႢ�ƒ�ƒ����ƒ�̊w�������㋭���ƒx�������w�K�����{���邱�Ƃɂ��ǂ̂悤�ȈႢ�������邩������ (Figure 18.1)
�E�����̖����Ɛ��k�̖����̈Ⴂ��adaptive behavior�ɋy�ڂ��e�������� (Figure 18.2)
18.3 Interaction and generalizability: Factors do not interact
��absence of interaction��generalizability�̐������������B�����2�v���Ɍ��ݍ�p���Ȃ��Ƃ������Ƃ���̗v������������̗v���̑S�Ẵ��x���ɂ����Ĉ��̉e�����y�ڂ��Ă��邱�Ƃ���������ł���B
���������ϓI��IQ�̊w�K�҂�ΏۂƂ��ĕ����̋����@�̌��ʂ��r�����ꍇ�A���̌��ʂ�low-IQ��high-IQ�̊w�K�҂ɂ���ʉ��ł��邩��t-test��one-way ANOVA����ł͌��ł��Ȃ��B������Figure 18.3�Ɏ������悤�ɕ�����IQ���x���Ŕ�r���邱�Ƃɂ���ʉ����\�ƂȂ�̂ł���B
18.4 Interaction and generalizability: Factors interact
��Figure 18.4�ɂ����̂悤�ȏꍇ�At-test��one-way ANOVA���g�p����ƁAtreatment�ɗL�Ӎ����o�Ȃ���������Ȃ��B�������A���̗�͈قȂ�\�͂̊w�K�҂ɑ��Atreatment�̉e�����قȂ邱�Ƃ������Ă���B
��interaction null hypothesis�́u�v��A�̉e���͗v��B����Ɨ����Ă���v�܂�A�u�v��A�͗v��B�̑S�Ẵ��x���ɂ����Ĉ��̐�����ۂ��Ă���v�ł���BA�~B interaction���L�ӂł͂Ȃ��ꍇ�ɂ́A�v��B�̑S�����ɂ����ėv��A�̉e������ʉ��ł��邱�Ƃ������B
18.5 Interpreting main effects when interaction is present
��treatment factor��Experimental��Control��2�������肷��ꍇ�A�A�������́uE��C�̕��ϒl�ɍ����Ȃ��v�ƂȂ�BFigure 18.5�Ɏ������悤�Ȍ��ʂ̏ꍇ�A�S�̂̕��ϒl�ɗL�Ӎ�������Ƃ������ʂƂȂ�B�������Agender��v���Ƃ��ē����ƁAE��C�ɍ�������̂͏����݂̂ł���A�j���ɂ����Ă�E��C�ɍ����Ȃ����Ƃ�������B�܂�Ateatment-by-gneder�f�U�C����p���邱�Ƃɂ��A���ݍ�p�����邱�Ƃ�������Atreatment�̉e����sex-linked trait�ł��邱�Ƃ�������̂ł���B
18.6 Statistical significance and interaction
�����ݍ�p�ɂ��Ă̓��v�I�L�Ӎ���F-test������߂����B�\18.1 (Figure 18.4) �̃f�U�C���ł�3�̉�����������Ă���B�A������1��2�͎���ʁA�A������3�͌��ݍ�p�ɂ��Ẳ����ł���B
18.7 Data layout and notation
��<��> 3�̎w���@ (factor A) �Ɛ��k�̐��� (factor B) ��v���Ƃ����������B3�~2�����ł��邽�߁A6�ʂ�̑g�ݍ��킹���z�肳���B����6�ʂ�̑g�ݍ��킹���lj� (observation X) �ɋy�ڂ��e����������B
Notation
��2�v�����邽�߁A���ꂼ��̃Z���̕��ϒl�̕\�L�ɂ�2�̉��t�����l���K�v�ƂȂ� (�\X�ް #jk)
���s���S�̂̕��ϒl�������Ƃ��͏W�c (aggregation) �������h�b�g�������� (��: �\X�ް#1 �E)
�S�̂̕��ϒl�� �\X�ް�E�E �ƂȂ�B����͑S�Ă�n�E�E �̊ϑ��f�[�^�Ɋ�Â��B
����ʓI�ɓ�v���̕��U���͂̊ϑ��l��X#ijk �Ŏ������Bj�͗v��A�Ak�͗v��B�Ai�͊e�Z���Ɋ܂܂��ϑ��l�̒ʂ��ԍ��B
18.8 A model for the data
���z�u���U���͂ł�2�̗v���̎���ʂ�������F��#j (effect of the jth level of factor A: ��#j = ��#j . - ��) �ƃ�#k (effect of the kth level of factor B: ��#k = ��.#k - ��)�B18.1�Ɏ������悤�Ȍ��������藧�B
�����֗��ōL�͈͂ɓK�p�\�ȃ��f���͏������G�ɂȂ��Ă���F����18.2
18.9 Least-squares estimation of the model�@���ǂ�������܂���ł���
��least squares�̊��: (a) �l��18.2�̌����ɓ��Ă͂܂邱�ƁA(b) X#ijk ���܂߂����̐��l��estimated values for nJK errors���K�肷��A(c) sum of squared errors���ŏ��ł���ꍇ��least-squares�����肷��ʁA��#j �A��#k �ƃ���#jk �A���Z�o�����ꍇ�B
��least-squared method: �����l�Ɨ\���l�̍���2��a���ŏ��ɂȂ�l�����߂���@�B
��sum of squared errors�̍ŏ��l�́A�\18.2�Ɏ�����Ă���12�p�����[�^�̌����ɓ��Ă͂߂邱�Ƃɂ��Z�o�����B
18.10 Statement of null hypotheses
���z�u���U���͂ł͗v��A�Ɋւ���A�������͎��̂悤�Ɏ������
H#01 : ��#1 . = ��#2 . = �c = ��#j .
����#j . ���ʂƓ������ꍇ�A��#j . - ��= 0 �ƂȂ�B�A�����������藧�ꍇ�A��#j �̓�#j . - �ʂƓ������Ƃ���A�S�Ẵ�#j ��0�ƂȂ�B(�v��A�ɂ��Ă̋A��������p. 495�̎��ɂ܂Ƃ߂��Ă���B)
���v��B�̋A���������A�v��A�Ɠ����B
����v���̏ꍇ�A����ʂɂ��Ă̋A�����������p�����g�ݍ��킹�������l������B
���A�����������p���ꂽ�ꍇ�A�ʂ̉���H#1 �����藧�Bp. 496. ���̉����͋A�����������p���ꂽ�ꍇ�ɂ̂ݐ��藧���̂ł��邽�߁A�A�������̊��p�ɂ���Ď����I�Ɏx�������B
���z�u���U���͂ɂ����Ď���ʂ̂ق��ɂ�����̉����A���ݍ�p�ɂ��Ẳ������c��B���ʂ��O���t�Ɏ������Ƃ��ɁA2�̐������s�ɕ`����Ȃ��ꍇ�A���ݍ�p�����邱�Ƃ��l���炦��B
�����ݍ�p�̋A������H#0 �ƁA�t�̉���H#1 �ɂ͕����̏q�ו������� (�� Table 18.3)
18.11 Sums of squares in the two-factor ANOVA
���ꌳ�z�u���U���͂Ɠ��l�ɁA�z�u���U���͂ł�sum of squares, degrees of freedom, mean squares, expected mean squares and F-ratio���g�p����B
���z�u���U���͂ł�: (1) variation resulting from difference among the J means for factor A, (2) variation resulting from difference among the K means for factor B, (3) variation due to the interaction of A and B, (4) variation of the observations #within cells��4��variation sources������B
Total sum of squares
���e�l�ƁA�S�̂̕��ϒl�Ƃ̍������v�������� (18.4)
Sum of squares for factor A
��nK�Ƀ�#j ��sum of the squared least-squares estimates���|�����l (18.5)
Sum of squares for factor B
��nJ = n.#k �ƃ�#k ��sum of the squared least-squares estimates���|�����l (18.6)
Sum of squares for the A �~ B interaction
������18.7
Sum of squares #within cells
��SS#w �Ŏ������ (18.8)
��SS#total = SS#A + SS#B + SS#AB +SS#w �Ȃ̂ŁA18.9�̓�����p����ق����e�Ղł���B
18.12 Degrees of freedom
���z�u���U���͂̂��ꂼ���SS�͎��R�x�Ŋ��邱�Ƃɂ��mean square�ɕϊ����鎖���ł���BSS�̎��R�x�́ASS����number of independent linear restrictions placed on these estimates���Ђ������l���琬��least-squares estimates�̐��ł���B
�����R�x��
| SS#A |
J - 1 |
| SS#B |
K - 1 |
| SS#AB |
(J - 1)(K - 1) |
| SS#W |
JK (n - 1) |
18.13 Mean squares
��MS�͎��R�x (v) �ɑ���SS�̊���: MS = SS / v
| MS#A |
SS#A / (J - 1) |
| MS#B |
SS#A / (J - 1) |
| MS#AB |
SS#AB / (J - 1)(K - 1) |
| MS#W |
SS#W / JK (n - 1) |
18.14 Illustration of computation for the two-factor ANOVA
�����̐߂ł́A���ۂɃf�[�^������ɂ���SS��MS���v�Z���Ă���B�f�_��T�X�R�A�Ɋ��Z���ꂽ�B
Sums of Squares
���X�e�b�v1�ŗv��A�̊e������effect����悳��A���̍��v�Ƀf�[�^�����|�����SS#A ���Z�o���ꂽ�B�X�e�b�v2��SS#B �l�ɎZ�o���A�X�e�b�v3��SS#AB ���v�Z���ꂽ�B
Degree of freedom and Mean Squares
���eSS�����R�x�Ŋ����MS���v�Z���ꂽ�B���ʂ�Table 18.4�Ɏ�����Ă���B
F-tests
����̎���ʂɂ��Ă̋A�������ƁA���ݍ�p�ɂ��Ă̈�̉������x�������ꍇ�A4��MS-value�̊��Ғl�̓�^2�Ɠ������Ȃ�B�����A�����������p�����̂ł���AMS-value�͍����Ȃ�AF-ratio�̒l�������Ȃ�B����F-ratio�ɂ���ċA���������x������邩�ǂ��������肳���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i����j
�f�B�X�J�b�V�������R�����g
�y�[�W�g�b�v�ɖ߂�
2008/05/09
Chapter 18, pp. 503-524
<�ǂݑւ����@�搔�̍��ׂɂ� ^ ���C�L���̉E�Ɍ���鉺�t�������̍��ׂɂ�# ��\�L���Ă���B
18.15 Expected Values of Mean Squares (p. 503-6)
��2�v���̕��U���͂̌v�Z�����̐����������Ȃ��A���̖ړI��F���z�e�X�g�̗��_�I�����𖾂炩�ɂ���B�P�v���̕��U���͂ł́A���ϕ������ǂ̂��炢�R�̋A�������̐^���������ɂ���Ċ��Ғl�����炩�ƂȂ�B
E (MS#w)
�����ϕ���w�̊��Ғl�́A���o���ꂽ���z�̕��ς���݂���B�Q�v���̕��U���̓f�U�C���ł���A��W�c����̕W�{�ɂ���ē���ꂽ���U�Ŋϑ�����A�ǂ̒��o�Z������������̕��U��^2 ��������B
��������W�c����n���o�����Z��J, K �̕��U����^2 �Ɖ��肵���ꍇ�AMS#w�͎�18.12�̂Ƃ���ƂȂ�B
���ϐ��������f�U�C���ł���A��18.13�̂Ƃ���B
�����Ғl�Ƃ��Ă�MS#w �܂�E (MS#w)�́A�p�����^�[�̌덷���肪�Ȃ��Ɖ��肵�A ��#��^2 (�܂��͒P���Ƀ�^2) �ŕ\�킳���B�Ɨ������Q�v���̃f�U�C��(Table 18.4)�ł́AMS#w��73.325�i��W�c���瓯���^�C�v�̊w�Z���m���璊�o�����Ƃ��̕��ϕ����j�ƎZ�o�����B���̒l�����ς�荂�����Ⴂ�����炩�ł͂Ȃ����A�덷���Ȃ����̂Ƃ����B
E (MS#A)
���P��̎�������� MS#A ���v�Z����A���Ғl�͕�����18.15��苁�߂���BMS#w�ƈقȂ�A�P��Ƃ������͍��������ϐ��ł���B
��nK = n#j., ��^2 =��#��^2 �͌���18.3 A-B (?)�̒��̌덷���̕��U�ł���AMS#w�ɂ���ċ��߂���B
����#j��j�̃��x�������v��A�̎���ʂ�\�킵�A��#j = ��#j. - �ʂ̂Ƃ��A
��#��^2 = ��#j ��#j2 / (J-1) �ƂȂ�B
��Table 18.4�̏ꍇ�� ��#��^2 �̐^�̒l��75�A��#1.=50, ��#2.= 54�̂Ƃ���= 1/2*(50+54)�A
J =2�An = 32�Ȃ̂ŁA�������� E (MS#A) = 843 �ƂȂ�B
�����ۂ̌v�Z�ł�E (MS#A)�����߂邱�Ƃ͕s�\�ł���A�d�v�Ȃ̂�E (MS#A)�ŕ\�킳�����̂��A�A���������̑��^���p���邩�ɊW���Ă���Ƃ������ƁB
�A���������^�ł���Ƃ������Ƃ́A��#1 = ��#2 = ... �Ƃ������Ƃ���A
E (MSA) = ��#��^2 + nK��#��^2 = ��#��^2 + nK (0) =��#��^2 �Ƃ����W�������B
�A�����������ł���Ƃ������Ƃ́A��#��^2 > 0 �ł���
E (MS#A) = ��#��^2 + nK��#��^2 > ��#��^2
E (MS#B)
��MS#B�̊��Ғl��18.16�̎��̂Ƃ���ł���i�O���[�v��J��K�ɒu�������j
���v��B�̎���ʂɂ��Ă̋A���������^�ł���Ƃ��AH#0: ��#k��#k^2 = 0
E (MS#B) = ��#��^2 + nJ��#��^2 = ��#��^2 + nJ (0) =��#��^2 �Ƃ����W�������B
���t�ɋA�����������p����̂ł���AMS#B��MS#w �����傫���͂��B
E (MS#AB)
��MS#AB�̊��Ғl��18.17�̎��̂Ƃ���B
�v��A�AB�̌��ݍ�p�ɑ���A�������́AH#0: ��#j��#k ( ����#jk )2 = 0 �ŕ\�킳��AMS#AB�̓�#��^2 �Ɠ����B�A�����������p����Ȃ�AMS#AB�̓�#��^2 �����傫���B
18.16 The Distribution of the Mean Squares (p. 506-9)
��18.4�̂悤�Q�v���̃f�U�C���ŁA2 x 3 = 6�Z���ɂ��ꂼ��32���i�v192�j�̒��o�ŁA����͔������� (replication of the experiment) �̊ϑ��ƌĂ��B
���ǎ��������Ȃ����ƂŁA2��A�R��c�ƁA�قȂ镽�ϕ������̂邱�Ƃ��ł���B
���ł́A�����̒ǎ��ɂ���ē����镽�ϕ����̕W�{���z�Ƃ́A�ǂ̂悤�ɂȂ�̂��H
���₢�𖾂炩�ɂ���O�ɁA18.2�̕��������f�������肳��Ȃ��Ă͂Ȃ�Ȃ��B
��JK�Z���𒊏o������W�c�͓����Ɖ��肵�A���U�������ł��邱�ƁB
����W�c�����K���z�����肵�Ă��邱�ƁB
The Distribution of MS#w
�����K���̉�������̂ł���A������Z���ɑ���n�̊ϑ��́A���K���z������#jk ���疳��ׂɒ��o���ꂽ���̂ł���A�Z���̕��U (S# jk^2) ���덷���܂܂Ȃ� (��^2 = ��#��^2) ���Ƃ��O��ƂȂ�B
�� S# jk^2 /��#��^2 ��n-1��Ƃ���J�C���敪�z�Ƃ��������Ȃ�B
�i�v��JK�ɂ���ċ��߂��镪�U�����l�j
The Distribution of MS#A
��MS#A �̕��z�́A�A���������^�ł���Ƃ��A
MS#A /��#��^2 �` ��#j-1^2 / J-1 �����藧�B
���A�����������p�����Ƃ��AMS#A /��#��^2�͔�S (non-centered) �J�C���敪�z�ƌĂ�A�����Ȑ������ς̍����i�E�����ւ́j���z������(Figure 18.9)�B
The Distribution of MS#B
��MS#B �̕��z���AMS#A�Ɠ��l�A�A���������^�ł���Ƃ��A
MS#B /��#��^2 �` ��#k-1^2 / K-1 �����藧�B
The Distribution of MS#B
���A���������^ (H#0: ��#k��#j ����#jk^2 = 0) �ŁA�v��A�AB�̌��ݍ�p���Ȃ��ꍇ�A
MS#AB /��#��^2 �` ��#(J-1)(K-1)^2 / (J-1)(K-1)�@�����藧�B
���A�����������p�����ꍇ�AMS#AB /��#��^2�͔�S�J�C���敪�z�ƂȂ�B
����Ȍ��ʂŏW��ɂ�����ASection 16.6�ŏЉ���Ƃ���A���ꂼ��̎��R�x��Ƃ���F���z�����߂�B
���A���������^�̂Ƃ��AMS#w�ɑ���MS#A�̔䗦�́A���R�x J-1�� JK (n-1) �ɂ��F���z���Ƃ�B�����ŁA�Q�v���̔��������ł�Figure 18.10 �̍����Ɏ������悤�ȁu�T�^�I�v�Ȋϑ��ƂȂ�A�E�����ւ̈�E��90-99�p�[�Z���^�C���̕��z�܂Ō���Ȃ��B
����A�A�����������p�����ꍇ�AMSA��MSw���傫���Ɨ\������A�T�^�I��F���z�̋Ȑ���`���Ȃ��i99�p�[�Z���^�C���̕��z����j�B
���v��B�܂���A�AB�̌��ݍ�p�ɂ��Ă̋A�����������p�����Ƃ������Ƃ́A���ϕ����̕��z��F���z�̉E�����ֈʒu����B�܂��A�����Œ��ڂ��ׂ����ƂƂ��āA��SF���z�ŗՊEF�l�i�^�e�̓_���j��Power�i��2��̌���Ƃ��Ȃ��m���j�������Ă���B
18.17 Hypothesis Test of the Null Hypotheses (p. 509-13)
�������ł́A���ϕ������狁�߂���R�̔䗦�iF��ƌĂ��j�ɂ��Ĉ����B
�@�@F#A = MS#A / MS#w�CF#B = MS#B / MS#w�CF#AB = MS#AB / MS#w�C
�������ł�F������A�P�v���̕��U���͂ɏ]���B
�@�E�܂��A�A�������̊��p��ƂȂ郿�l�̐������߂�B
�@�E�댯���J-1, JK(n-1) ��F���z��100 (1-��) �p�[�Z���^�C������S�Ă̐����܂�
�@�EF#A = MS#A / MS#w�̒l���댯�l#1-��F# j-1, #JK (n-1)�̒l����ꍇ�A�A�������͊��p����A�����菬������̑�����B
��jTable 18.4�̎����ł́A2 x 3�̃f�U�C���Ō�192
�@�v��A�F
�����R�x��1, 186
�@�@�����p���5% (��P��̌���20���1��)
�@�@�� #.95F#1, #186 �` 3.92 �̂Ƃ��A�������͊��p�ƒ�߂�B
�@�@��F#A = 4.954�ƎZ�o����A��l��荂���������߁A�A�������͊��p�B
�@�@��X#1��X#2�̕��ς�5%�����ŗL�ӂɈقȂ��Ă���ƌ��_�B
�@�v��B�F
�@�@�����p��� #.95F#2, #186 �` #.95F#2, #120 �` 3.07
�iF���z�\�ɑΉ����鎩�R�x���Ȃ�����X�I�� n = 120�Łj
��F#B = 7.711�ŋA�������͊��p����A����� #.999F#2, #186 �` 7.32��������邽�߁A0.1%�����ŗL�Ӂi�A���������^�ƂȂ�m����1�^1000�����j
��Figure 18.12�ɂ���ĕ���X#jk�̑��ݍ�p�ׂĂ���B���_���m�肷�邽�߂ɂ́A�v��A�AB�̎���ʂ�F���肵���悤�ɒ��ׂ�K�v������B
�@�E���ݍ�p���Ă��Ȃ��i�A���������^�ł���j�Ȃ�AF#AB�͌��߂�ꂽ���R�x�Łi��S�ł͂Ȃ��jF���z�����Ă���͂��B
�@�@��F#AB = 21.980 / 73.325 = .300�ŗՊE�l (= 3.07) ������邽�߁A���ݍ�p���Ă��Ȃ����Ƃ��m�F�����B
��Fig 18.12��Mean Plot���AFigure 18.13�̃n�R�q�Q�E�O���t�̕����A�݂������Ԃ�ǂ������Ă���i�����w�Z�̏�ʌQ��negative skewness���Ă���A�Ƃ��j�B
18.18 Determining Power in Factorial Designs (p. 513)
��Section 15.26�`29�̂P�v���ɂ�镪�U���͂ƁA�ϐ�����Ă��镡���v���̃f�U�C���ł́A����͂̎Z�o�͂悭���Ă���B
�E��`���ėp�����铝�v�l (nK, J, ��#j, ��#��^2) �͕ς��Ȃ��B
��j4 (�N��w) x 3 (�s������) �̃f�U�C���A�e�Z���Ɍ�12����
�E18.18B�������A�@��#��= 1.414
�@�EvB = 2 ����A�t�^��Table G�Ɋ�Â�v#e = 132
�@�E�\������錟��͂� .56
18.19 Multiple Comparisons in Factrial ANOVA Designs (p. 514-15)
���P�̗v���ɂQ�i�K�����Ȃ��̂ł���A���d��r (MC) �͗]���ȍ�Ƃł���B����A�v���̎���ʂ̒��ɂR�ȏ�̃��x�����܂܂��Ƃ��́A�ǂ̃y�A�ňقȂ��W�c����̕W�{�ɂ�镽�ρi�L�Ӎ�������j�Ƃ�����̂�MC�������Ȃ��K�v������B
��Chapter 17�̌Œ�v���ɂ��MC�̎菇�Ř_���I�ɐ����ł���B�B��̈Ⴂ�͎�������(marginal mean)��p���A��ׂĂ��镽�ςɂ͊ϑ������l������Ă��邱�ƁB
��Table 18.4�̗�ł͗v��A�͂Q���x���Ȃ̂ŕs�v�B�v��B�͂R���x���ŏ���ɂ��敪�Ȃ̂Ńg�����h����(Section 17.19)���D�܂����B
�@�E�v��B�̑ΏƂɊ܂ޕ��ς̒�`�͑O�͂� (��17.7, Sec 17.8)
�@�E�ΏƂł݂���W���덷�� 17.8A�̎���Section 17.10
�@�Et�l�̗ՊE�l���߂鎩�R�x��v#e = 186
�@�E�g�����h���͂ł�contrast coefficient �͕t�^��Table N���狁�߂���B
��J = 3�Ȃ̂ŁAX�̕��ςR��p. 514���̕\������` (-1, 0, 1) ��������B�@
�E���ꂼ������������ʁA^�Ճn�b�g#linear = 5.928, S#^���ް = 1.514
t = 3.915
�@�@�� v = 186�̗ՊE�l��0.1%������3.37�܂ł�����A���`�g�����h���͂��疾�炩�ȗL�ӂ��݂�ꂽ�B
�E�m�F�ŋȐ��g�����h���͂������Ȃ����ꍇ�At = -.294�ƂȂ�5%�����ł��L�ӂƂ͂Ȃ�Ȃ������B
�������A��ׂĂ���R�̕��ςɘA���������肳��Ȃ��ꍇ�i��F�����w�Z���k�̒��o�ł͂Ȃ��A�ٖ����Ԃ̃O���[�v���Ƃ�����j�AK�̕��ύ��̗L�Ӑ����݂�B
�@�����@�ɂ�POC, Dunn, Dunnet Scheffe�@�Ȃǂ�����B
�@���X�`���[�f���g���ɂ�铝�v��@�ł���ANewman-Keuls��Tukey������B
18.20 Confidence Intervals for Means in Two-Factor ANOVA (p. 516-17)
���������ςƃZ�����ς̐M����Ԃɂ��ẮASection 11.18�̎菇�ɏ]���B
�@�@S#x = ��MS#e / "n" �i�����ł�n�͊ϑ�����������j
��jTable 18.4
�@�@S#x = .874
�@�@#.975t#186 = 1.973
�@�@.95CI = (50.12, 53.57)
�@�����̂��Ƃ���A�����������Ȃ��������w�Z�ł̕��ϓ_�́A95%�̐M����Ԃ�
52.87�`56.32�_�̂ǂ����ɗ��������B
�@���v��B���AS#x ( = .1.070), t�l�̗ՊE(1.973)��c�����邱�ƂŁA�M����Ԃ��킩��B
���Z�����ς̐M����Ԃ͌��ݍ�p�̉��߂ɂ��𗧂��A68%��̐M����Ԃ��g���̂��K�B
18.21 Three-Factor ANOVA (p. 517)
���Q�v���̕��U���͂̊T�O�𗝉�����A�R�ȏ�̗v�����܂f�U�C���𐳂����z�u���āA���߂ł���悤�ɂȂ�B�V���ɉ����T�O�Ƃ��Ă͂R�v���̌��ݍ�p���l������B
���ϐ������ꂽ�f�U�C���ł���A�S�v���̑g�ݍ��킹�������ő����B
�@�E�R�v���̌��ݍ�p�́A�Q�v���̌��ݍ�p�ƓƗ����Ă���A�O�҂����҂ւ̈��ʊW�͂Ȃ��B
�@�ETable 18.6�ɂQ�v���E�R�v���̌��ݍ�p�̈Ӗ����������Ă���B
18.22 Three-Factor ANOVA: An Illustration (p. 517-19)
���e�X�g�p�t�H�[�}���X�ɂ�������F
|
T1 |
T2 |
|
M |
F |
M |
F |
| A1 |
10 |
10 |
10 |
10 |
| A2 |
10 |
10 |
10 |
10 |
| A3 |
10 |
10 |
10 |
10 |
�iA1�j�s�������̂��߂̋����@
�iA2�j�����I�ȋ���
�iA3�j�s���ɂ����鋳��
�iS�j���ʁiM / F ���疳��ׂ�10�������o�j
�iT1�j����\�̓e�X�g
�iT2�j���w�\�̓e�X�g
���s�ΐ���ʂ̃��f����p.518�O���̂V�̎��ŕ\�킳��A���Ɍ�����Ă���e�������킹�����v��0�������B
��Table 18.6
�Epanel I�͑S12�Z���̊ϑ����ʂƁA�v��A�̎���ʂ����
�Epanel II�́A�e�v���̎���ʂƁA������Q�v���̑g�ݍ��킹���ׂĐ���
18.23 Three-Factor ANOVA Computation (p. 520-21)
���R�v���̕��U���͂ɂ��v�Z���@ (panel III)
Step 1)��#j �̗\���l��p���āA�v��A�̎���ʂɂ�镽���a (SS#A) �����߂�B
2), 3) ���l�Ƀ�#k �ƃ�#l �̗\���l�ŗv��T��S�̕����aSS#T, SS#S�����߂�B
4), 5), 6)�ʁX�ɂQ�v���̕��U���͂��R���Ȃ����悤�ɁA����#jk�A����#jl�A����#kl
�̗\���l��p���āA�Q�v���ɂ����ݍ�p�̕����a(SS#AT, SS#AS, SS#TS)�����߂�B
7) �R�v���̕����a(SS#ATS)�����߂�B
8) �Z�����̕��ϕ���(MS#w)�����߂�B
�@��MS#w�Ɋւ�鎩�R�x(v#w)�����߂�B
Results
��panel IV�ɂ݂���悤�ȕ��U���͕\�ŕ\������B
�@�E����̗�ł́A�v��A, T, S����P�Ƃ̎���ʂ͂Ȃ������B
�@�@���R��anxiety condition �ɂ͓��v�I�ȗL�Ӎ��͂Ȃ��B
�@�@������Ɛ��w�̃e�X�g���ʂɂ��A�S�̕��ς���̗L�Ӎ��͂Ȃ��B
�@�@�����ʂɂ��L�ӂȈႢ���Ȃ��B
�@�E�v��AT��AS�̑g�ݍ��킹�ŁA���ݍ�p�͂Ȃ������B
�@�@���v��A�ɂ́A�R���x���ǂ���Ⴂ���Ȃ��Ƃ������Ƃň�ʉ��ł���B
�@�E�B��A�v��TS�ԂŌ��ݍ�p���݂�ꂽ�B
�@�@���j���ԂŁA�e�X�g���ʂ����e�i����E���w�j�ɂ���ĈقȂ�(Figure 18.14)
�@�@�@�����q�͌���e�X�g�ŁA�j�q�͐��w�e�X�g�ň��������(?)�B
18.24 The Interpretation of Three-Factor Interactions (p. 521-22)
���R�v������̌��ݍ�p�͗L�ӂł͂Ȃ������B
�@������̗�ŁA�ł����ړI�ɉ��߂ł�����@��anxiety condition ����ʓI�Ɉ����A
�c��Q�v��TS�̌��ݍ�p�����ł݂��ꍇ�B
�����ƂȂ��Ă�����ݍ�p�ɂ͗v��A����̉e���͂Ȃ��̂��H
�@�����łɂR�v������̌��ݍ�p���Ȃ����Ƃ��킩���Ă��邽�߁A�v��A��������Â����Ă���ƍl���Ȃ��Ă悢�B
������Figure 18.12�ŕʂ̗v��(grade level)�������A�w�N�Ԃň�т������ʂłȂ���A���̂Q�v���{G�̂R�v���Ō��ݍ�p���Ă��邱�ƂɂȂ�B
18.25 Confidence Intervals in Three-Factor ANOVA (p. 522)
����n�⎩�R�x�́Amean, s#x, t�l�̕W���덷�ɊW����B
���ϑ����̓Z���≺�ʃO���[�v�̕��ς̐M����ԂɁA
�@s#x�͗v�����x���̕��ςɊւ���M����ԂɕK�v�ł���B
��s#x�̋��ߕ��́Ap. 522�̎��ɂ���Ƃ���ŁA������ "n"�Ƃ́A���̗v���̃��x�����ɂ��B
�@���v��A: nKL, �v��B: nJL�C�v��C: nKJ�Ƃ��������
��jTable 18.6 �ł�A(3) x B(2) x C(2)
�v��A = 10 x 2 x 2 = 40
�v��B / C = 10 x 3 x 2 = 60
�@�����ꂼ������ɑ������ƁA�v��A�� s#x = .826�C�v��B�EC��s#x = .674
�@���v��A�̐M����Ԃ́A���̗v���Q���1.23�{�傫���Ƃ炦��K�v����B
�@���Z�����ς̐M����Ԃ�10�̌��Ɋ�Â����߁A����ɍL�� (s#x = 1.65)�B
18.26 How Factorial Designs Increase Power (p. 522-23)
������v������ݍ�p�ɂ��ĊS�̊O�ɂ������Ƃ��Ă��A�ł������̂���v���̉e���̌���͂����߂��ł����v�����܂߂邱�Ƃ��]�܂����B
��jTable 18.7 �P�v���̃f�U�C��
�@�@�E�v��A��MS�����̗v���ɉe������Ă��Ȃ��B
�@�@���ϐ������ꂽ�f�U�C���ł͏�ɁA����ʂƊ֘A����ȊO�͑S�Č덷�ϗʂƂȂ�B
�@�@�EF�䂪Table 18.4�Ɣ�ׁA�ቺ�Ap�l���オ���Ă���B
�@�@���덷�ϗʂ��Q�v�������傫���Ȃ邽�߁B
18.27 Factrial ANOVA With Unbalanced Designs (p. 523-24)
���v���̐������߂�ɂ�����A��n���ψ�łȂ��ꍇ�A�����a�̋��ߕ������G�ɂȂ�B
�����^�̃f�U�C���ł́A����̒������{���Ȃ�����A�e���̍��݂���F������\��������B
�@���Z�����̌��̈Ⴂ�����Ȃ������قǖ��ɂȂ�Ȃ��B
�������҂����ӂ��Ȃ���Ȃ�Ȃ����Ƃ́A���v�ň�����肪�A���炩�ɂ��������ƍ����Ă��邱�ƁB
���ł��T�d�ȃf�U�C���Ă�I�тA����e���ɂ��đ��̃��f���ł͖��炩�ɂ��Ȃ������������o���邱�Ƃ����߂���B
18.28 Chapter Summary (p. 524)
�E���U���͎͂��p���������A�{�͂ł͂Q�v���ȏ���������B
�E���ݍ�p�ł̑Ώ�
�����ݍ�p���Ȃ��ꍇ�́A�e�v���ł̈�ѐ�
�E���ݍ�p�ł̉��߂ɂ�����\�����@
�E�P�v���̃f�U�C����茟��͂����܂�ꍇ
�E�O��Ƃ���邱��
���Z���̓Ɨ����A����ׂȒ��o�A���K��
���ϐ��̂Ƃꂽ�f�U�C���ł̐��K���E�����U���ւ̊挒��
�E�ϐ����Ƃ�ĂȂ����͂ł̉��߂̕��G��
18.29�ȍ~�͏ȗ��@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����j
�f�B�X�J�b�V�������R�����g
��unbiased�Ƃ͕s�ΐ���̂��ƂŁA�ϑ���n�ł͂Ȃ��An-1���g���ĕ��U�����߁A��W�c�̕��U�ɂ��߂����������ꍇ�̗p��ł���B
���Ђ��}�̓ǂݎ����K�����ibox��25~75%�܂ł�\���A���̒����̍ő�l��box�̒�����1.5�{�j
��central�͋A���������^�̂Ƃ��Bnoncentral�͋A�����������p���ꂽ�Ƃ��B
����v������v���̂ق����L�ӂɂȂ�₷���B�iF�l���傫���Ȃ�A����ɂƂ��Ȃ��āAp�l��������ip.523�j�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�X�{�A����j
�y�[�W�g�b�v�ɖ߂�
2008/05/23
Chapter 19, pp. 535-547
<�ǂݑւ����@�搔�̍��ׂɂ� ^ ���C�L���̉E�Ɍ���鉺�t�������̍��ׂɂ�# ��\�L���Ă���B
19.1 Introduction (p. 535)
���{�͂ł̎�ȖړI
(1) �ϗʌ��� (random-effect) ���܂߂����U���̓��f���̗��_�I�w�i
(2) �������ʂ̕��U���̓��f���̊T��
���v��������q�\���ɂȂ��Ă���f�U�C���ł́A���x�ȕ��U���͂̓K�p�ɂ��Ă�
19.2 The Random-Effects ANOVA Model (p. 535-37)
���ϗʌ���(random-effect)�́A�Œ肳�ꂽ����(fixed-effect)�ɂ�镪�U���f���ƈقȂ镔�������邪�A�ގ��_�������̂�15, 18�͂ł̒m�������̗̏͂����������邾�낤�B
���Œ���ʂƕϗʌ��ʂ̈Ⴂ
�E�Œ胂�f���F��ȊS��J���W�c�Ƃ���n�̊ϑ��ւ̎���ʂ̐��v
�@�@���������x���C���������Ƃ����W�cJ�Œ������J��Ԃ��ꍇ
�E�ϗʃ��f���FJ���x���ł̒��o���A�������J��Ԃ����тɈقȂ�ꍇ
�@�@����K�͂ȃf�[�^�̎�œK�p�ł���
�@�@���ϑ����ׂ�n�̒��o���A���̓s�x�A����ׂɑI���
���Œ���ʃ��f��(��#j = ��#j - ��)�������ł���悤�ɁA�ϗʌ���(a#j = ��#j - ��)���e���͂���B
�EJ��#j �̊��S�ȃf�[�^�Z�b�g�Ȃ�A�J��Ԃ��ɂ��Œ肳�ꂽ���ʂ��݂���B
�E�ϗʌ��ʃ��f���ł́Aa#j �̌��ʂ͔C�ӂ̃T���v���ɂ�鐄�v�����݂��Ȃ��B
��Bennet (1972) �ɂ��ϗʌ��ʃ��f���̐����F
��j���t�̈Ⴂ�ɂ�鎙���̓lj�͈琬�ւ̉e�� �� �ϗʃ��f���̓K�p
�E�C�ӂ̒��o���畽��(��#j)���A���U(a#j)�A�\������镽��(��#j�n�b�g)����̕��U�����߂�
���ϗʌ��ʃ��f�����T�O�I�ɐ�������ɂ́A
�@ ���������Ƃ���鋳�t�̕�W�c���O��ɂ���
�A �lj�̓e�X�g�ŗ^���链�_(��)�̕��ς���#j
�B i�Ԗڂ̐��k��j�Ԗڂ̋��t����^�����链�_��X#ij �Ƃ���
�C �B�ɑ��āA�S���k�ɋ��tj���^���链�_���̕��ς���#ij �Ƃ���
�� �����܂��A19.1, 19.2�̓�����������
�� 19.2�̎�����A�ϗʌ��ʂ̕��U���̓��f���̓�����������(��19.3)
��j
�E��W�c����̕��� (��) = 30 (�S�Ă̋��t���S���k�̓lj��e�X�g���̓_�����ꍇ��)
�E���t9����^����ꂽ���k�̓��_���ς�4�_�������� (a)
�E���k49��(?)�́A���t9�̓��_���ς��8�_�Ⴉ���� (��)
�� 19.3�̎��ɑ�������
�@X#49 = �� + a#9 + ��#49 = 30 + 4 -8 = 26
�������ł̊S�̓�#j �̂��
�� a#j �Ƃ́A�ϑ������ϗʂ̃�#j�����W�c�̕��σʂ̕��������������l���������߁A
�@ a#j �̕��U (��#a^2) ���ړI���̂��̂ƂȂ�B
19.3 Assumptions of the Random ANOVA Model (p. 537-38)
��19.3�̎��������O��Ƃ��āA
1. �ϗ�a#j �͓Ɨ����Ă���A���K���z���Ă��邱��
2. ��#ij �̌덷���������l�ɁA�Ɨ������K���z���Ă��邱��
�������A���ň����Ă���u���t�̉e���v�ɂ��Ă̌����ŁA�ϗʌ��ʃ��f�����f�[�^�̐��m�ȋL�q�����Ă���̂ł���A
1. ���σ�#j �͕�W�c�̕��σʂ̎��ӂŐ��K���z���A���U�̓�#a^2 �Ŏ������B
a#j �̌��ʂ� a#j ʯ� = X#j�ް �| X.�ް �Ŏ�����
2. ���tj�ɂ��S���k�̕��ϓ��_X#ij �̓�#j ���ӂŐ��K���z���A���U�̓�#��^2�Ŏ������B
�S�Ă̒lj�ɂ͏�L�����Ă͂܂�A������U�������肳��Ă���Ƃ���
�@��#ij �� e#ij = X#ij - X#j.�ް �ɂ���Đ��肳���
19.4 An Example (p. 538-39)
�������Ŗ��Ƃ���Ă���̂́A���t�ɂ��lj��e�X�g�̓��_���U��#a^2�̈Ⴂ�ƁA�������t�ɂ�鐶�k�̓��_�̈Ⴂ��#��^2�B
���Q�i�g�̒��o�Ńf�[�^�����W (Table 19.1)
�EJ�̃��x���Ɋ�Â����v����ׂɒ��o����
�@�� ��ł́A���t5������
�E�e���x���i���t�j����n�̊ϑ��𒊏o����
�@�� ���_�I�ɕ�W�c����͖��������A
�����ł�20�`30�A����̗�ł͐��k7���𒊏o
���P�v���̕ϗʌ��ʃ��f���̏ꍇ�A�v�Z���@�͌Œ���ʂ̕��U���̓��f���Ɠ���(15��)�B
�EJ�̕��ςɂ�镪�U���畽�σ�#j �̕��U��#a^2 �����߂��A
�EX#ij �̕��U�����#��^2 �����߂���
19.5 Mean Square Within, MS#W (p. 539)
���Œ���ʃ��f���ł́AJ�̓��_�T���v�����番�Us#j^2 �����߂��A����͕s�Ε��U��#��^2 (�܂��̓�^2) ������
�E��n�͓��������߁A�����J�̕��U�̕��ς͕s�Ε��U�ɍœK�Ȑ�����@������ (15.8)�B
�@�� �T���v�����ł̕��U�̕��ς� MS#W (mean square within)�ƌĂсA���ߕ���19.4�̎��̂Ƃ���B
��MS#W �͎��̂悤�Ȑ���������B
1. MS#W �̊��Ғl�͕s�Ε��U��#��^2�Ɠ����� E (MS#W) =��#��^2 �ƕ\�킷�B
2. MS#W�̕��U�́AJ�̃O���[�v�ɑ���n�̖���ג��o�Ɋ�Â��Ă���A
�ȉ��̎��ŋߎ��l��������B
MS#W �`��^2 ��#j (n-1) ^2 / J (n-1) = (��#��e^2 / ��#e) ��^2
��16.4�Ŏ������Ƃ���A��#��e^2 = ��#e ��K�p�����19.5�̎��̂悤�ɒP��������A
E (MS#W) =��#��^2 ���ؖ��ł���B
19.6 Mean Square Between, MS#Between (p. 539-40)
��15, 18�͂ň������ϐ������ꂽ���U���̓f�U�C���̏ꍇ�A�ϑ��������ς����������MS#Between ��0 �ƂȂ����B
�� J����O���[�v�Ԃ�MS#Between �́A��n�ɂ���ďd�ݕt����ꂽ���ύ��ɂ���Ă̂��肳���B
��19.6�̎��Ŏ������悤�ɁAMS#BETWEEN ��J����T���v�����ς���̕��U (s#x^2) �� n�{�������̂ł���AMS#Between �̊��Ғl��19.7�̎��̂Ƃ���ɂȂ�B
��MS#Between�͒��ׂ����v���̕��U��#a^2��n�{���邱�Ƃ�MS#W�ɂł���ȏ�̐��v���\
�@�� ��������#a^2 = 0 �̂Ƃ��́AMS#Between ��MS#W �͋��ɓƗ����ă�#��^2 �̒l���Ƃ�B
���T���v���Ɋ�Â�MS#Between �̕��z��19.8�̎��Ŏ����Ƃ���B
�@�� J-1�̎��R�x�Ɋ�Â�������l���A�萔 (��#��^2 + n��#a^2) / (J - 1) �Ŋ|�����l
�@�� �Œ���ʃ��f���ƈقȂ�A��#j �ɈႢ���������Ƃ��Ă��p����萔�͓���
��Table 19.2��Table 19.1�̃f�[�^��p���āAMS#BETWEEN��MS#W �̋��ߕ����T���������́B
�@�� MS#BETWEEN = 164.55, MS#W = 33.81
19.7 The Variance Component (p. 540-42)
���T�O���[�v�Ԃ̑����� (X�ް.) ��31.94�ŁA��#a^2 = 0 �̂Ƃ��A�lj��e�X�g�̓��_�͕�W�c�����肵�����σ� ( = 31.94) �̎��ӂɐ��K���z����͂��B
�@�W������ ��MS#W = ��33.81 = 5.82
��MS#BETWEEN �̊��Ғl��19.7�̎��ɂ������Ƃ���B
�@�s�Ε��U��#a^2 ��MS#Between��MS#W ��p���āA19.9�̎��̂Ƃ��苁�߂���B
��Table 19.9��F����ɂ��A���t�ɂ�铝�v�I�L�Ӎ����݂�ꂽ�B
�@�� �v���̕��U���� (variance component) �͕s�Ε��U�̋��ߕ��ɂ���������#a^2 = 18.68
�����t��v���Ƃ����W�c�Ɋ�Â����ς̕��U��#a2 �͕��U�����ɓ������A���捪�����W�c�̕W���� (= 4.32) �����߂邱�Ƃ��ł���B
�����ɃT���v�����O�E�G���[�ɂ��AMS#W ��MS#BETWEEN �����傫���ꍇ�A��#a^2�̗\���l�͕��̒l���Ƃ�B�������A���U�͕��̒l���Ƃ邱�Ƃ͂Ȃ����߁A0�ɓǂݑւ���B
19.8 Confidence Interval for�Ѓ�^2 /��#��^2 (p. 542-43)
���P���z�u�̕ϗʌ��ʃ��f���̏ꍇ
(1) �ǂ�����ă�#a^2 /��#��^2 �̐M����Ԃ����̗\���l���� (��#a^2 ʯ� /��#��^2ʯ�) �Ɉʒu����̂�
(2) �ǂ�����ă�#a^2 = 0 �̉������������̂�
����#a^2 /��#��^2 �ɂ�����1-���̐M����Ԃ́A19.10�̎��̂Ƃ���ɋ��߂���B
��Table 19.1�ł̃f�[�^�Ń�#a^2 /��#��^2 �ɂ�����95%�����̐M����Ԃł���AF���z�\����97.5%�����ł̗ՊE�l��T���A�����2.5% (�c��̗L�ӊm��?)�ł�F�l��19.11�̎��ɑ�����ċ��߁A��A�̕��ϕ����AF�l��19.10�̎��ɑ������B
�@�E�Ⴉ��́A95%�̐M����Ԃ� .071�`5.65
�@�@�� �l�̏㉺�����L���A��G�c�ȗ\���ł���Ɖ���
�i��#a^2 �̓�#��^2��1�^10����5�{����l�̂ǂ����ɕ��z�j
�@�@�� ���肩���m�ȗ\����ɂ́AJ��n�̗������傫���Ȃ��Ă͂����Ȃ�
���P�̗v���̂����郌�x����������W�c���Ƃ��Ă���Ƃ������Ƃ͍l���Â炢�B
�@�� �ϗʌ��ʃ��f�����g�����ƂŁA��#a^2 = 0 ���ǂ����̐����͂̂���_�ɖ𗧂�
�E�葱���Ƃ��āA�A����������#a^2 = 0 �𗧏��邱�Ƃ� ����^2 = 0 �ł��邩���ׂ�̂Ɠ���
�@ ��) Table 19.2: �Q�̕��ϕ��� (Between, Within) �Ŋ���Z�����Ƃ���19.12�̎�
�@�@�� F = 164.55 / 33.81 = 4.87 �i#.99F#4, #30- > 4.02 �Ȃ̂ŁA1%�����ŗL�Ӂj
19.9 Summary of Random ANOVA Model (p. 543-44)
���i�ύt�����ꂽ�j�P�v���̕ϗʌ��ʃ��f���ŁA��ȃ|�C���g�� Table 19.3 �ɂ���Ƃ���
�E�Œ���ʃ��f���F �덷���� (��#ij) ���A�Ɨ�����0 �𒆐S�Ƃ��鐳�K���z(NID)���Ă���
�E�ϗʌ��ʃ��f���F ��#j ���A�Ɨ�����0 �𒆐S�Ƃ��鐳�K���z(NID)���Ă���
�@�� ���K���Ɠ����U�������肳��A���ƃÂ̍\���v�f���݂��ɓƗ����Ă��邱��
�����K�������肵�Ȃ��ꍇ�̌Œ���ʃ��f���ɂ��āi15�́j�A����قǏd�v�Ȗ��͂Ȃ��A���U���قȂ�ꍇ�ł��A���������ł������قǐ[���Ȗ��Ƃ͂Ȃ�Ȃ������B
�@�E�ϗʌ��ʃ��f���ł����l�̂��Ƃ������邱�Ƃ͂��܂�m���Ă��Ȃ��B
�@�@�� �v�����x���̐�J��������قǂɁA���̐[�����͂Ȃ��Ȃ��Ă����B
19.10 The Mixed-Effects ANOVA Model (p. 544-47)
���Œ���ʂƕϗʌ��ʂ�g�ݍ��킹���������f���́A���ؓI�����ŗL�p��������
�E���Ȃ��Ƃ��P���̌Œ�E�ϗʌ��ʃ��f�����܂ނƂ��p������
�@�� �ŏ��łQ�v������
��jTable 19.4 (Roney, 1975)
10���̋��t�A7�����̐��k��ג��o���A3��ނ̎w���@�������Ȃ����ꍇ
�E�Q�̗v���i�w���@�A���t�j���ꂼ��Ŏ����
�@�� ���ʂ���A�R�̎w���@����W�c����̒��o�Ƒ�����ׂ��ł͂Ȃ�
�@�� �������{�҂̈Ӑ}�ł́A�Q�̎w���@�����ꂩ�œ����Q���D�ʂ��������肾����
�@�� �������A���t10���ɂ��e�����݂��A��ʉ��ɖ�����������
�E���_�Ƃ��āA���������w���@�ɂ͑��ΓI�ɗD�ʂȁi�Œ肵���j���ʂ��݂��A
�@����ג��o�ɂ���Ċϑ��������t10������́A�ϗʌ��ʂɂ��e�����݂�ꂽ�B
�����̂悤�ɁA19.13�̓������O������ƂȂ�\�����f�����A�������ʃ��f���ƌĂԁB
�EX#ijk �͂Q�v�����m��j�Ek�Ԗڂ̌�_�ɂ���Z���̊ϑ�
�E�� �͑S�ϑ����W�c�Ƃ���S�̕���
�E��#j ��j�Ԗڂ̌Œ���q���x���ł̉e���x (��#j �|��)
�Eb#k ��k�Ԗڂ̕ϗʈ��q���x���ł̉e���x (��#k �|��)
�E��b#jk �͑O�̂Q��g�ݍ��킹�����ݍ�p [ ��#jk �| (�� +��#j + b#k )
�E��#ijk ��j�Ek�Ԗڂ̃Z���ɂ݂���c������
������19.13�̍������f���ɂ́A�O��ł͂Ȃ�������Ƃ��Ď��̂��Ƃ���������
1. �v�����̌��ʂa�����ꍇ�A0�ƂȂ�B
2. �v��b�̑S�̕��ς�0�Ɉʒu����i���o�������t10�������̕�W�c�Ɋ܂߂āj�B
3. ���ݍ�p��b��S�č��킹���Ƃ��A0�ƂȂ�B
4. ����j�̕�W�c�́A���ς�0�Ɉʒu����B
�� ���̐���ɂ��A�Œ���ʂƑ��ݍ�p�Ƃ��f�[�^�Ԃō��킹���Ƃ����E����邪�A
����̐���̕��ς��������o�����ꍇ��0�Ƃ͂Ȃ�Ȃ�
����b��0�ɂȂ邱�Ƃ͂Ȃ��B
�E�قȂ�����ɂ���Ă��ꂼ��K������ג��o���ꂽ��b�ް#1., ��b�ް#2.�ł��邽��
�E�o���̕��ύ��̕��U�́A���ݍ�p�̐������܂�
�@�� �������f���ł̕��ϕ����̊��Ғl���������邱�ƂŁA���Ԃ�]���ł���
19.11 Mixed-Model ANOVA Assumptions (p. 547)
���������f���ɂ��19.13�̎��ɂ́A�ȉ��̑O����B
1. �ϗʌ��ʂ͒ʏ�A���ς�0�Ɉʒu���鐳�K���z�������B
2. ���ݍ�p��k��j�̕��ς��Ƃ���0�ňʒu���鐳�K���z�ƂȂ�B
3. �덷�������܂����K���z�������A�v��b�⑊�ݍ�p��b�Ƃ͓Ɨ��������U�����Ƃɂ������ϒl��0���Ƃ�B
���Œ���ʂ̎���ʂɂ��ċA��������������Ƃ��A�S�Ԗڂ̑O��Ƃ��āu���ʐ��v�����݂���B��W�c����̕��U�Ƒ��ւ��������Ƃ��A���ʐ��������B
4. ���ʐ��̐����́A������W�c���番�U���Ă���Œ���ʂ̕��z�����o������Ƃ킩��B
�@�� �S�Ă̕ϐ��y�A�������̑��ւ�`���Ă���͂�
�����ʐ������肳��Ȃ��Ƃ��A�Œ���ʃ��f���ł�F���茋�ʂ��ɂ��Ȃ�A����̌��������N�����\���������Ȃ邪�ACollier et al. (1967) �ɂ����������P�[�X�͂܂�B
�@�� p�l����萳�m�ɎZ�o����C������������
Null Hypothesis�i�A�������j
| �A������ |
|
������ |
�@1. �Œ���ʃ��̑��a��0
�@2. �ϗʌ���b�̕��U��0
�@3. ���ݍ�p��b�̕��U��0 |
��
��
�� |
���a��0�ł͂Ȃ�
���U��0�ł͂Ȃ�
���U��0�ł͂Ȃ� |
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����j
�f�B�X�J�b�V�������R�����g
�E�Œ���ʃ��f���́A���͂Ɏg�p����v���̐����i��ʂɂ͌Q������Ȃǁj���L�������Ȃ��ꍇ�ɗp���A�ϗʌ��ʃ��f���́A���̗v���̐����i��ʂɂ͔팱�ҁj���A��W�c����̐�����z�肷��ƁA�����l������ꍇ�Ɏg�p����B(�Q�lpp.535-536)�B���Ƃ��A���ʂƂ����v���͂��̐����i�j�q�Ə��q�j�͌����Ă���̂ŌŒ���ʃ��f�����g�p���邪�A�{���̗�̂悤�ɁA���k�̓lj�͂ɋy�ڂ������̉e��������ꍇ�̋�����v���ɂ����ꍇ�A�����͖����ƍl������̂ŁA��W�c���烉���_���ɒ��o�����ƍl������ϗʌ��ʃ��f����p����BSPSS�ł�univariate�̕��͂ɌŒ�v���ifixed
factor(s)�j�ƕϗʗv��(random factor(s))����ʂ��ē��͂���悤�ɂȂ��Ă���B
�E���肩���m�ȗ\���邽�߂ɂ̓T���v���T�C�Y�Ƌ��ɃO���[�v���������Ȃ���Ȃ�Ȃ��Ə����Ă������̂������[���B�A���A�T���v�����ƃO���[�v���̗����𑽂����邽�߂ɂ́A�c��ȎQ���҂��K�v�ɂȂ�Ȃ����낤���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i����A�X�{�j
�y�[�W�g�b�v�ɖ߂�
2008/06/06
Ch. 19 �㔼�ipp. 547�`�j
19.12 Mixed-model ANOVA computation
���@MS��df�̎Z�o���@�́A�Œ胂�f���ł��A�ϗʃ��f���ł��Amixed ���f���ł������ł���BF�䂪�v�Z�����Ƃ��̂݁A�Œ胂�f����mixed���f���͈قȂ�B
���@�A���Amixed factor�ł̌Œ���ʁiMethod�j��MS�̊��Ғl��3��������Ȃ��Ă���̂ɑ��A�Œ胂�f���ł�2�������琬�藧���Ă���ip. 506��Table 18.5��p.545��Table 19.4���r����ƁA���ꂪ���炩�ł���j�B�������A�����_�����q�̎���ʁA���ݍ�p�A�덷�ɂ��Ă�MS�̊��Ғl�͓������B
���@�ϗʈ��q�̋A�������ׂ邱�Ƃ́A�����q���Œ肳��Ă���Ƃ��̋A�������ׂ�̂Ɠ������B
Variance Components
���@variance component�̃�ʯ�^2�i�����_�����ʂɂ������W�c�̐����́A���ϒl�̕��U����j�́A�ϗʈ��q�ɂ��ĕ���邱�Ƃ������B
19.13 Multiple comparisons in the two-factor mixed model
���@���d��r�͌Œ���q�ɂ̂ݗp�����Ach. 17, 18�ŏЉ�����@�Ɠ����ł���B�A���AMS�̌덷�݂̂���╡�G�ɂȂ�iMS�̌덷���ϑ����Ŋ�����j�B
19.14 Crossed and nested factors
���@�����܂Ō��Ă������q�͑S��crossed�ł��邪�i�����q�ɂ����đS�Ă̐�����combination������j�A���̈��q�̒��ɓ���q�ɂȂ��Ă���ꍇ������B�Ⴆ�A�S�Ă̎������@���S�Ă̊w�Z�Ŏg�p�����Ƃ��ɂ́A���@���w�Z��crossed�ł���B�������A������@�͊w�Z1, 2�݂̂Ŏg�p����A�ʂ̕��@���w�Z3, 4�Ŏg�p�����ꍇ�ɂ́A�w�Z�͕��@�̓���q�inested�j�ɂȂ��Ă���B
���@�܂�A���qA�̊e���������qB��1�̐����ł�������Ȃ��ꍇ�A���qA�͈��qB�̓���q�ɂȂ��Ă���B
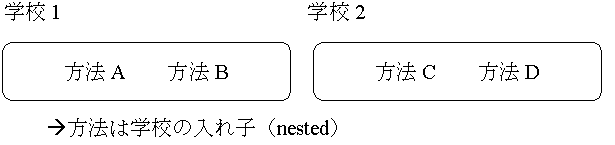
���@����q�̈��q�͂قڏ�ɕϗʈ��q�ł��邪�A�ϗʈ��q����ɓ���q�ł���킯�ł͂Ȃ��B
19.15 Computation of sums of squares for nested factors
���@�\19.5�ɂ��Ă̌v�Z�Ⴊ�f�ڂ���Ă���B
19.16 Determining the sources of variation in the ANOVA table
���@����q�̈��q�́Across������q�Ƃ̂��ݍ�p����B
19.17 Degrees of freedom for nested factors
���@����q�̏ꍇ�ɂ́Adf�͓���q�̐��~����q�̒���df�ł���B5�l�̐搶�����ꂼ��2�̊w�Z�ɂ���ꍇ�ɂ́A2�~(5-1)��8�ɂȂ�B
19.18 Determining expected mean squares
���@MS�̊��Ғl���v�Z���邽�߂ɂ́A2�̃��[��������B
(1) MS�̊��Ғl�̍\���v�f�icomponents�j�͓���̌��ʁ{(a) ����̌��ʂƕϗʌ��ʂ̌��ݍ�p�A(b) �������̌��ʂɓ���q�ɂȂ��Ă��郉���_�����ʁB
(2) �\���v�f�̌W���́A���̍\���v�f�ɑ����Ă��Ȃ��S�Ă̈��q�̐���������v�Z�����B
19.19 Error mean squares in complex ANOVA designs
���@F����̕���ɂ́A���q�Ɋ܂܂�Ă���A�ΏۂƂ���ϐ��ȊO�̂��̂�S�Ċ܂ށie.g., A���ΏۂƂ���ϐ��̏ꍇ�AF = (A + B + C) / (B +C)�j�B�A���������^�̂Ƃ��A����ƕ��q�͓����p�����[�^����̓Ɨ���������l�ł���B
19.20 The incremental generalization strategy: inferential "concentric circles"
���@Table 19.5�ł�method�̌��ʂ͗L�ӂł͂Ȃ����A�����f�[�^���g�p���Ċw�Z�̕ϐ�������Table 19.4�ł͗L�ӂł���i�܂�A�w���Ƌ��t�Ɉ�ʉ��ł�����ʂ͗L�Ӂj�B�Ȃ����̂悤�Ȃ��Ƃ��N�������̂��낤���H����́A�������ꂽ�ϗʈ��q�͈ÂɌŒ���ʂƂ��Ĉ����Ă��邽�߂ł���B�܂��A�M�����Ȃ��悤�Ȍ��ʂ��o��Ƃ�������i�ϗʌ��ʂƂ��Ă���v�����������ꍇ�ɂ͗L�ӂ����A�Œ���ʂƂ��Ĉ������ꍇ�ɂ͗L�ӂɂȂ�Ȃ��A�Ȃǁj�B
���@���̂悤�ȏ�concentric circles��p���邱�Ƃʼn���ł���B�܂��Areplication error�ȊO�̑S�Ă̈��q���Œ���ʂƂ��Ĉ����B�����ŗL�ӂ������ꍇ�Ɍ���A�����q��ϗʌ��ʂɂ���B
���@�Ⴆ�ATable 19.5�ł̏ꍇ�ɂ́A�܂��w����ϗʌ��ʁA�w�Z�Ƌ��t���Œ���ʂɂ��A�����ŗL�ӂł���A���t��ϗʌ��ʂƂ���B����ɂ���āA���k�Ƌ��t�̕�W�c�ɂ��Č��ʂ���ʉ��\���ǂ�����]���ł���B�����ł��L�ӂł���A�w�Z��ϗʌ��ʂɂ���B
���@Figure 19.2�ł́Auniverse #0�ł����random source of variation�͖����A�f�[�^���p�����[�^�Ƃ��Č��Ȃ����߁A���k�A���t�A�w�Z�ɑ��Ă̐������o���Ȃ��B����͋L�q�I�Ȍ����Ƃ�����Buniverse #1��ANOVA��t-test��\���B�w�Z�Ƌ��t���Œ肷�邱�ƂŁA���ʂ�����̋��t�Ɗw�Z�ɂ����鐶�k�̕�W�c�Ɉ�ʉ��ł��邩�ǂ����ׂ邱�Ƃ��o����B
19.21 Model simplification and pooling
���@Table 19.5�̂悤�ȏꍇ�ɂ́A�덷��df���������̂œ���̌��ʂ��傫���Ȃ��Ă��邩������Ȃ��B���̂悤�ȏꍇ�ɂ́AANOVA���f�����������A�P�������邱�Ƃ�F�䂪1�����̂��̂����f������폜���邱�Ƃ��ł���B
���@Table 19.5��Mt:s��F���1�����ł���B�]���āAMt:s�̃�ʯ�^2��0�ƌ��Ȃ����Ƃ��o����B�]���āA��������f������폜���邱�Ƃ��ł���B�덷��df��������̂ŁAF�̊��p�l�͉�����B�������AM�~s�̌��ݍ�p�͗L�ӌX���Ȃ̂ŁA���f������폜���Ȃ������ǂ��i�폜����ƁA���p�l���}���ɏ㏸���邽�߁j�B
���@�A���A���f����P���������ꍇ�ɂ́A�P��������O�ƌ�̕��͂��ڂ��A�ǂݎ�����߂ł���悤�ɂ���ׂ��ł���B
19.22 The experimental unit and the observational unit
���@observational unit��experimental unit�̋�ʂ����Ȃ���Ȃ�Ȃ��Bobservational unit�́A�����ɂ����Ď��ۂɓ����f�[�^�̂��Ƃł���Bexperimental unit�Ƃ́A���̗v���Ƃ͓Ɨ����Ċ��蓖�Ă�����̂ł���B
���@�Ⴆ�A�����ɂ����treatment�������_���Ɋ��蓖�Ă��A���̋������ɂ͕������̐��k������Ƃ���B�팱�ғ��f�U�C���ł́Aexperimental unit�͐��k�ł���Aobservational unit�̓e�X�g�Ȃǂ̓��_�ł���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�X�{�j
�f�B�X�J�b�V����&�R�����g
�ETable 19.7 �ŁAA, B, C�̃��f�������邪�A�R�̗v���i���t�C�w���@�C���k�l�j�܂ł��ׂ����l�������A���f��C�������Ƃ��]�܂����ƍl������B���̈���A�傫�ȗv���Ŋ����Č��ʁE�e�������o���ꂽ�Ƃ��Ă��A����q�ɂȂ��Ă���ʂ̗v���ԂŊ��ɑ��݂��Ă��邩����ł��Ȃ����߁C���f��A�CB�̂悤�ȃf�U�C���͕s��������B
�E�v����x���𑽂��ݒ肷��ΗL�ӂɂȂ�₷���Ȃ邽�߁A��ʉ��ɑς�����ϑ������厖�ƍl����Ƃ���͑O��Ɠ��l�B�܂��A���߂����G�ɂȂ肷���Ȃ��v���̐��ɍi���Ē����v��𗧂Ă邱�Ƃ��d�v�Ƃ����Ă���
[�Q�l�F�c���E�R�� (1989).�w���[�U�[�̂��߂̋���E�S�����v�Ǝ����v��@�x]�B���̖{�ɂ��ƁA�����Ă��R�v���̗v���ɂƂǂ߂��ق����f�[�^�̉��߂���薾�m�ɂȂ�Ƃ��Ă���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����j
�y�[�W�g�b�v�ɖ߂�
2008/06/20
Ch. 20, pp. 572-85
20. 1 Introduction
���������f���̕��U���͂ɂ́A�u���肩�����ϗʁv�f�U�C���ł̕��͂��悭�݂���
�E�����O���[�v�́A�قȂ����ŁA���������̕ϗʂ�������ꍇ
�E�ʂ̕��@�Ƃ��āA�قȂ鑪��@����ŕ\�킵�ėp���邱�Ƃ��ł���i�W�����_�Ȃǁj
�@�����肩�����ϗʂƌĂ�闝�R�Ƃ��āA����@��͈�x�Ƃ͌���Ȃ�
���w�K�����ŁA�Ώۂ��������Ƃɉ��x�����_��ʒm����邱�Ƃ�����
�@�������ł́u�����v�������T�^�I�Ȃ��肩�����ϗʂ̗v��
�@�����ɂ����B�����Ⓑ���I�Ȓ����ŁA����̕ϗʂ������Ώۂ��炻�̓s�x�̂�ꂽ���肩�����ϗʂɂȂ肤��i�����ł́u�N��E���������v���v���Ƃ�����j
�����Z�₻��ȍ~�̓��B�x�e�X�g�ł�T-score�Ō��ʂ��\�킳���B
�E���肩�����ϗʂ̕��U���͂ł́A���炩�̏W�c�i�n��A�w�Z�A���� ���j��v���ɕ��͂������Ȃ��A���B�x�̐��ڂ����R���A�L�ӂȋN��������̂��m�邱�Ƃ��ł���
20. 2 A Simple Repeated-Measures ANOVA
�������Ƃ��P���Ȃ��肩�����ϗʃf�U�C��
�E�Q�̎���ʂ�����
�E�]�����Ă���v���̓����_���i����̒����ɂ�钊�o����A���̒������W�c�ֈ�ʉ�����������j
�E���肩�����ϗʂ̗v���́A�T�^�I�ȌŒ�v��
�E�ϑ��l�� XST�iS�Ԗڂ̑Ώۂɂ��āAT��ڂ̑���j�ŕ\�킳��A������20.1�̂Ƃ���ƂȂ�
���Ⴆ�A10�̑Ώۂ���5��̑��肪�����Ȃ��Ă���Ƃ���
Table 20.1�F
�E���R��͑Ώ�(Subject)�̕����a�A�^�e��͎���(Trial)�̕����a�����߂��A�����đ��ݍ�p�ɂ��Ă�Ch. 19 (Table 19.4) �̎����狁�߂���
�E���M���ׂ����ƂɁA�Z��������̊ϑ�����1�ł��邽�߁A�Z�����ł̕��U�̎��R�x��0�ƂȂ�
�@���Z���̊ϑ��l���Z�����̕���
��3�ӏ��i�v���Q�A���ݍ�p�P�j���畽�ϕ���(MS)�̗\���l��Table 20.1�̒��قǂ���
�E�v��T��MS�\���l�́A��#sT^2 + S��#T^2
�E���ݍ�p��MS�\���l�́A��#sT^2
�� �v��T�ɂ��F��� MS#T / MS#sT = 65.95 / .372 = 177.18
�� #1-��F #(T-1),#[(T-1)(S-1)] �Ɣ�r���A�������ŋA������H#0��L�ӂȂ̂����肷��
�� ���ݍ�p�Ɋւ���A�������̓�#��^2���g���Ȃ����߁A����ł��Ȃ�
20.3 Repeated-Measures Assumptions
���O��ɂ́A�ʏ�̕��U���́i�Ɨ������ϑ��ԂɁA�����U���Ɛ��K�������肳���j�ɉ����A���ʐ������߂���B
�E�v��T�̓����U�����F�߂��A�ϗʃ��x���Ԃő��ւ���������A (T-1)��(T-1)(S-1)�̎��R�x(df)���Ƃ�F�l�������ɕ��z���� (compound symmetry: �Q���g�ݍ��킳���Ē��a���Ă���(?))
�@�� �ߔN�ł́A�K�v�ȏ�ɐ����������Ƃ��ؖ�����Ă���
Huynh & Feldt (1970, 1979):
�Enominal�i���ڏ�́H�jdf��F���z�������Ɉʒu����A���ʐ��͖��������
�� ���ʐ��̔���͊��o�I�ŁA���_�I���������G�Ȃ��߁A���p��͐��w�I�ɋ��߂邱�Ƃ��Ȃ�
��Huynh & Feldt�̒��:
�E�Â����ʐ�����̎��R�x��\�킹��
�@�� ���ʐ������肳���Ƃ��A�Â̗\���l�͗��z�I�ɂ�1.0�A�ň��ł� 1 / (T-1) �̊Ԃ��Ƃ�
�@�� �Â͋��ʐ������@�����Ƃ��̕�ŋ@�\���Ă���
��jTable 20.1: ��= 1�i���ʐ��ɖ��͂Ȃ��j
�� �ϗʃy�A�̑��ւ��Ђǂ��قȂ�ꍇ�A�Y���y�A�̕��ύ�(MD)�̕��U���߂��Ƃ͂����Ȃ�
�@�i���̏ꍇ�A�Â�1.0�������AF�l�̗ՊE���㏸���Ă���͂��j
��Huynh-Feldt�̏C���́A���肩�����ϗʂ̕��U���͂̂��߂ɍ��ꂽ���v�v���O�����ɂ́A�W���I�ɂ݂���
�E�L�ӊm����nominal df (T-1), (T-1)(S-1) ����Z�o����A�[���ɉߏ��]������邱�Ƃ͂܂��Ȃ�
�E�Q���x���̂��肩�������͂ł���A��ɋ��ʐ�����
20.4 Trend Analysis on Repeated-Measures Factors
�����͂ɘA����������Ƃ��Atrend analysis �͑��d��r����L�x�ƂȂ�
�Etrand analysis�̓K�p�P�[�X��Ch. 17, Sec 17. 19���Q��
�E�v��I�ɒ���Δ���`�����A����ʂɓ��v�I�L�Ӑ����Ȃ���Γ��ʂɎg����
�����߂ɂ��Ă�Sec 17. 19���Q��
�ETable 20.1�̗�ł́A���`�ƎO���̌X���͗L�ӂɂ݂�ꂽ���A�Ǝl���i�����́j�X���݂͂��Ȃ�����
�@�� ���`��O���X���͊w�K�ɂ��肪���ŁA���O���t��������炩
��trend analysis �ɂ́Acompound symmetry �⋅�ʐ��̑O��͕K�v�Ƃ��Ȃ�
20.5 Estimating Reliability via Repeated Measures ANOVA
�������A���ʂő���덷��������Ȃ��Ȃ�A���ʂ͈�݂��Ȃ��͂�
�E�Ó�����O��ɂ���A����ɂ͂Ȃ�炩�̐M����������
�E�����A�]���ϐ��ɑ���덷�ȊO�܂܂�Ă��Ȃ��̂ł���A�M�����W����0�ƂȂ�
�@��j�lj��e�X�g�ɂ�����Q�̎w���@�Ŕ�r����:
�@�@���ۂ̃e�X�g���ȒP�����āA���k�S��������
�@�@�� �M�����W���͔��ɒႭ�A�e�X�g����͎w���@�ɂ��Ĉ�̗D�������ł��Ȃ�
���M�����W���Ƃ́A����덷�ł͂Ȃ����_����\�킹��x����������
�E�]���ϐ��̌덷���U�̔䗦�́A1-��#xx
�@�� ���s���Ă����Ȃ������茋�ʂ����S��v�ł���A��#xx = 1.0
������Table 20.1�̗�ŁA���肩�����ϗʂ�Trial�ł͂Ȃ��e�X�g���ڂ�]���҂Ƃ�����A�M�����W���͎�20.2�ŋ��߂���
�@�� ���s�I�ɂ����Ȃ�ꂽ����`���Ƃ̑��� �� �����ł̐M�����W��
�@��j1.0���瑊�ݍ�p(sT)�Ɨv��s�i���k�j�̕��ϕ��� (MS#sT, MS#s) �̔䗦�ō����������l
Reliability and Length: The Spearman-Brown Formula
�������A���s�e�X�g�Ȃǂ̑���Œ����ɈႢ������Ƃ��́A��20.3�̏C��������p����
�E��#xx�͏C���O�̌W��
�EL�͐V���ȑ���ƁA���X�����Ȃ�������Ƃ̔䗦
���M�����̍�������́A�\�z�����M�������������o�邱�Ƃ�����
�@��Spearman-Brown�̎��́A���^�C�v�̍��ڂ�]���҂��������Ɖ��肵���Ƃ��̒l�����߂�
20.6 Repeated-Measures Designs With a Between-Subject Factor
�����肩�����ϗʂ̕��U���͂ɂ́A�Ώۂ�����q�\���ɂȂ��Ă���v�����݂���
�E���肩�����ϗʂ̗v���͔팱�ғ����� (within-subject effect)
�E����q���Ƃ̗v���͔팱�ҊԌ��� (between-subject effect) �Ƃ��Đ��������
�� �O�͂܂ł�between-subject effect�Ƃ��ďЉ�Ă���
��within-subject�ł͌��ʂ̗L�Ӑ����A�Ή��̂���t����Ɏ�����@�Œ��ׂ�
�E���肩�����ϗʂ̓��_�Ԃő��ւ�����Ƃ��AF����̕���͒ቺ����
�@�� �L�ӂƔ��f����̂ɕK�v�ȕ��ύ�(MD)�͏��Ȃ��Ȃ�i����͂͏オ���Ă���j
�@�� ���_�I��within-subject ��between-subject��������͂�����
���ł��P���ȃf�U�C���ibetwee-, within-subject effect �P���j
�E�s�A�W�F�̎��ʔ���^�X�Nx4�iWithin: liquid, mass, weight, volume�j
�E�`�B���[�h x2(Between: consistent, inconsistent)
�En = 16 x 2�i�e�`�B���[�h�̃O���[�v�Łj
|
Tasks (Within) |
| C. Modes (Between) |
Liquid |
Mass |
Weight |
Volume |
| Consistent |
16 |
�� |
�� |
�� |
| Inconsistent |
16 |
�� |
�� |
�� |
��Table 20.2
�㕔
�EMS�̗\���l�F(1) �e�����̂��́A(2) ����q�A�܂��͉��f�������肩��������
�Ebetween- �� within-subject �ł́A�ʁX�̌덷���������Ă���
�@�� �ʏ�́Awithin-subject�̌덷���ϕ��� (E MS: error mean square) ��������
������
�Ecommunication mode(C)�Ŕ�ׂ��Ƃ��Aconsistent�̕���inconsistent���L�ӂɍ���(p = .007)
�EC��Task(T)�Ƃ̑��ݍ�p�݂͂��Ȃ������̂ŁAtask�̂S���x���Ńp�^�[���͈�т��Ă���͂�
��Huynh-Feldt �� �� .845��1.0�����������
�@�� df�ƁA����ɂƂ��Ȃ�p�l�̏C�����K�v
�@�� �����ł̂ł́AT, C x T, T x s �ɉe������
�E���ʁA�ϑ����ꂽF�䂩��͏C���ɂ��e���͂Ȃ������itask: .022 �� .016�j
�@�� �̎悵���f�[�^�����ʂ������̂ƒ������قȂ��p�l���㏸����
�@�� ���ۂ̂Ƃ���A�킸���ɕω�������x
���ǂ̃^�X�N�Ńp�t�H�[�}���X�����܂��\�킹�Ă��邩�m��ɂ́ATable �������Q��
�ECh 17�̎菇�Ɋ�Â��AMS#error�����߂� ( = 2.23)
�EE MS�͊ϑ����Ŋ��� ( = ��2.23 / 32 = .263)
�@�� �Ⴂ���ؖ��ł���̂́A���ɒ[�̒l�̂�
�@�@�ideaf�̐��k�ɂƂ��āAliquid task ��mass task �Ɣ�ׂ�Ɛ��т��ǂ��Ȃ��j
20.7 Repeated-Measures ANOVA With Two Between-Subjects Factors
���O�߂܂ŁATable 20.2�̗�ł͂����ЂƂ̔팱�Ҋԗv�� (Age) �����Ă��� �� Table 20.3��
�E��C. mode �O���[�v�ɂ́A9�`15�˂̔N��v��4�i�K�ƁA�S������deaf���܂�
�@�� �����ɂ́A2 x 4 x 4 ��C. mode, age, task �̂R�v���Ńf�U�C������Ă���
�����ʂQ
�EF�䂪Table 20.2�����傫���Ȃ��Ă���
�@�� ����̒l�������Ă���A�lj��v����Age����L�ӂȌ��ʂ����肳���
�@�� Huynh-Feldt ��= 1.0 �idf������K�v�Ȃ��j
�����ݍ�p�̌���
�EC x A�ɗL�ӂȑ��ݍ�p�݂͂��Ȃ�����
�@�� �O���[�v���̔N��w�͈���Ă��A�����̌��ʂ�Ԃ��Ƒ����Ă悢
�EA x T�ł͑��ݍ�p���݂�ꂽ
�@�� �^�X�N�E�p�t�H�[�}���X�ɂ͔N��̈Ⴂ���l���ɓ����ׂ�
�@�� Table �����̃O���t��
�E�O���t����A�R�̃^�X�N�͔N��w�ł̎����悤�ȌX����\�킷
�E�������Avolume �����͈قȂ����p�^�[���������Ă���
�� ���ݍ�p�̗L�ӂɂȂ������������Ƃ߂�
�E�R�v�� C x A x T �ɂ͑��ݍ�p�݂͂��Ȃ������̂ŁAA x T�Ԃ̍�p��C. mode �O���[�v�̊Ԃł���ʉ����đ�������
20.8 Trend Analysis on Between-Subjects Factors
���v��Age�͗\�z�ǂ���L�ӂł�����
�@�� �A�����̂���v���ł��邱�Ƃ��W���Ă���A�g�����h���͂̌��ʂ�������d��r���]�܂���
Ch 17�̎�17.7A�̎菇�܂��A
�EX�ް��SD������, MS #error�͊ϑ����Ŋ��� [person�̐��ł͂Ȃ�( = 32)]
�� ��W��(contrast coeffecient)��Appendix��Table N
��17.8B����A
�E�Δ�W���̕W���덷 (s#��ʯ�) �����߂�
�Et-ratio�it�䗦?�j�� ��ʯ� / s#��ʯ� �ŋ��߂�
�Eerror MS�̎��R�x�́A�����ł�24
�E�g�����h�͐��`�������L�ӂɔF�߂�ꂽ
20.9 Repeated-Measures ANOVA
With Two Within-Subjects Factors and Two Between-Subject Factors
�����肩�����ϗʃf�U�C���́A�팱�Ҋԁ^�팱�ғ��̗v����������ł��܂߂邱�Ƃ��ł��A�v���̎�ށi�����_���^�Œ�C���肩�����^����q�j�����Ȃ�
�� ����܂Ŗ������Ă����A�u2���� �팱�ғ� �v���v���܂߂ĕ��̓f�U�C����g��
�@�� �S�̈قȂ�덷�������߂���
�����肩�����v���ɂ́A���ꂼ���error MS�ŕʁX�ɋ��ʐ������߂���
��jTable 20.4
�E�������[�h(M)�F 2���x���݂̂ł��邽�߁A��� ��= 1.0�i�����̕K�v�Ȃ��j
�E�^�X�N(T)�F��= 1.0�i�����̕K�v�Ȃ��j
�ET x M�F ��ʯ� = .989�i�قږ������Ă���j
���v��M�͕ϓ�����10�i�����+�ւ���Ă��鑊�ݍ�p�̍��v�H�j�A���v������8�܂�
�E�v��M�̎���ʂ͗L��
�E�Q�̗v��C��T��g�ݍ��킹�����ݍ�p(C x M, T x M)�́A�Ƃ��ɗL�Ӑ��Ȃ�
�E�v��A�Ƃ̑��ݍ�p(A x M)�ł͗L��
�@�� ��N�w��deaf�Ɋւ��āA�����̈����o�����ɂ���Ă͓��_���e������
�@�� ���̗v��A�������ꍇ�A��������_���Ă����\����������
���R�v���iC x A x M, T x A x M�j�ƑS�S�v������̑��ݍ�p�ɂ͗L�Ӑ��݂͂��Ȃ�����
�@�� A x M�̑��ݍ�p�p�^�[������ʉ����đ�������
20.10 Repeated-Measures ANOVA Versus MANOVA
�����肩�����ϗʂ̕��U���͂́A���ϗʕ��U���� (MANOVA) ����ł������Ȃ����Ƃ��ł���
�EMANOVA�͋��ʐ����m�ۂ���Ȃ��Ă��A�����ȑ���̌����m���������Ă����
�EStevens (1986, p. 414):
�@����̌��̑Ώ��Ƃ����_�ł́A���ϗʕ��͂��]�܂����Ƃ��������͂Ȃ�
�� �C�����ꂽ��ϗʂ̌�����g�����ƂŁA�����Ȍ덷�m���͕\����̂�
�E���̑I�������݂�A����͂Ǝg���₷������������
�@�� ���ʐ����i�T�˂ł��j���肳���A���肩�����ϗʕ��͂̕�������͂�����
�@�� ���ʐ��̊�� ��ʯ� ? .75 ����
�EO'Brien & Kaiser (1985):
���ʂȍu�K�⌤���܂����l�ł��Ȃ�����́A���肩�����ϗʕ��͂̕����킩��₷��
20.11 Chapter Summary
�� ��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����j
�y�[�W�g�b�v�ɖ߂�
2008/07/25
Ch. 21, pp. 593-607
21.1 The Functions of ANCOVA (p. 593)
�������U����(ANCOVA)��Fisher��1993�N�ɕ��U���͂Ɖ�A���͂�g�ݍ��킹�čl�Ă������́B
�E���ϗ�(covariate)�Ƃ����t���ϗʂ������邱�ƂŁA�ǂ�ȕ��U���̓f�U�C����ANCOVA�ɂ�������B
�E�ړI�͈ȉ��̂Ƃ���F
�i�P�j���v����͂����߂�
�i�Q�j�덷�����Ȃ�����
���O�҂ł悭�p�����A�����̖���ג��o���Z�p�I�ɍ���ȏꍇ�̌덷�̏�����
���[�������f�[�^��ג��o�f�[�^�ɕϊ�����킯�ł͂Ȃ�
�E�f�[�^���W�ŕs��ۂ������Ă����Ԃ��яo����~�ύ̂悤�ɁA������F�������ׂ��ł͂Ȃ�
��An Illustration
�E���w�Z20������U�w�N��Ώۂɒ���
�E�C�ӂ�10�����R���s���[�^�x���v���O�����ɂ��앶�w���������Ȃ��A���Ƃ�10�����]���̃J���L��������
�E�N�x���ɋ��ʉۑ��^���A��勳�t������ׂ�������100�_���_�̍̓_������
���w�Z������50�`120���̃T���v�����W�܂������A�w�Z�̗̍p�v���O�����͖���ׂɐU�蕪�����Ă���
�@��Table 21.1�̗�ŁAANOVA��ANCOVA�ɂ�镪�͂������Ȃ�
21.2 ANOVA Results
��ANCOVA�ł́A�d��A���͂�g�����h���͂̂悤�ɏ]���ϐ���Y��p����i�����U��X�ŕ\���j
������܂ł̊e�팟��Ǝ����悤�ɁA�ϐ��̓����U���A�Ɨ����A�덷���z�̐��K�����O��
21.3 ANCOVA Model
������E�Ɠ���C�̎w���@���܂�School�̂��Ƃ�mean��\��
�ESchool�ɂ��덷�����͎����Q2�ԖڂȂ�A�Ⴆ��#21 = Y#21 - Y�ް#1�D
�@����ʯ� �͗\���l�̎c���i�덷�j
��Table 21.1�̕\���ɂ��ẮASchool�̊ϑ��������킩��Ȃ��ꍇ�B
�E���������炩�̕ϐ�X���]���ϐ�Y�ɑ��ւ���Ƃ������Ƃ͂��肤��
�@���w��(e.g. IQ)�̍����w�Z�ł���A���B�x�e�X�g�ō����l�ƂȂ�X���͗\�z�����
��21.2
�����_�I��ANOVA���f���Ō덷��ʯ�#ij ���Q�̓Ɨ��ϐ��ɐ藣�����@������
����ʯ�#W ��X��Y�̊W�����������A�W���̗\���l�F
���Œ���ʃ��f����ANOVA�͌Œ���ʃ��f����ANCOVA�ƂȂ�
�@���@��21.3, 21.3A
�E���̎��ł�Y�͏]���ϐ��ł͂Ȃ��AY�Ƌ����U���܂߂ė\�����ꂽY�Ƃ̍�
��ANCOVA�̑���덷�̐�Βl��'�́A�W�̂Ȃ������U�i��#XY = 0�j���捞�܂Ȃ�����ANOVA��菬����
�E�����P�v���ł����ANCOVA�̂ق���ANOVA��茟��͂�����
21.4 ANCOVA Computations: SS#Total
��Y�̕��U��X�Ƃ̉�A�W��r^2����\������A�������ꂽ�����a(SS'#total)��21.4�̎����瓾����
21.5 The Adjusted Within Sum of Squares, SS'#W
���팱�ғ�(Within)�ɂ��Ă����l�ɁA��21.5�ɂ���Ƃ��蕽���a�����������
����21.5�������Ȃɂ́A�W��r#W�����߂đ������
21.6 The Adjusted Sum of Squares Between Groups, SS'#B
���팱�Ҋ�(Between)�̒����ςݕ����a�́A�S��(Total)����팱�Ҋ�(Within)�����������ċ��߂�i��21.7�j
21.7 Degrees of Freedom in ANCOVA and the ANCOVA Table
����O�ЂƂ�����df�̋��ߕ���ANOVA�Ɠ���
�� �����U�̂��߁Awithin source��df ���ЂƂ���
�E�����ςݕ��ϕ���MS'#B / MS'#W ��F���z�̂Ƃ�df��J-1��n.-J-1
��Table 21.2�̗�ŁAANOVA��X�CY�̑��ւ��̂炸���͂������߁A�A�������͊��p���Ȃ��������A21.1, 21.2�̎���p�����ꍇ�A0.1%�����̗L�Ӑ���������
21.8 Adjusted Means, Y-bar'#j
��mean�����ĉ��߂���ɂ́A��21.8��p����Bb#W�̓�W�i��A�W���̌X���j�̗\���l
��b#W�̋��ߕ��͎�21.9
��������ł́AANCOVA��Method�̎���ʂ�ANOVA�̂Ƃ����傫���Ȃ��Ă���
�@��School E�̃J���L�������D�ʐ���
�@������E�|C�̗D�ʂ����Ȃ�A����ʂ͏��������������
������ɏd�v�Ȍ��ʂƂ��āA�덷���U������\���̐��m���������Ă��邱��
�@����'�ƃÂ̕��U�ɂ��Ă͎�21.10�Ő��������
21.9 Confidence Intervals and Multiple Comparisons for Adjusted Means
���M����Ԃ�݂���ɂ́AMS'#W�����̂܂ܗ��p�ł���i��21.11�j
��mean�������O��ňقȂ�ꍇ�́A���ꂾ�������O�Ɍ덷���܂܂�Ă���Ƃ�����
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����j
�y�[�W�g�b�v�ɖ߂�
2008/08/21�@�y�ŏI��z
Ch. 21, pp. 593-607�i���j
21.10 ANCOVA Illustrated Graphically
�������U���͂��g���Ӗ��́AX�Ɋ܂܂�鑪��m�C�Y����Y�̒l�����邱��
�@�� Figure 21.1: �S�Ă̌Q��X����̉e�����Ɖ��肵�AY�̐���������Ȃ�
��School���Ƃ�E / C�Q�������Ă����߂ɂ��������T���v�����O�ł̌덷
�@�� C�Q��IQ���킸����E�Q��荂������
��Table 21.1 �ň�����ANOVA�����Y�ް#1��Y�ް#2�i��������mean�j�ɂ́A�L�Ӎ����݂��Ȃ�����
��X��Y�̑��ւ͍����AE�Q�ł���� r =.931, C�Q�� r=.805, within-Group�� .852������
��ANCOVA�ł́A��A�����̌X�������Q�œ������Ƃ��O��ƂȂ�
�@�E��W�c����݂���A�W����b#W = 1.73 �ƂȂ�
�@�@�� �����l��Y�ް#2�Ɋւ��ẮA�����ɂ����3.06�Ⴍ�Ȃ�͂�
��e#11��Y#11�̌덷��\�킵�A��A����b#W�܂ł̃^�e�̋����Ŏ������
��X��Y�ɑ��ւ��݂���ꍇ�AANCOVA�ł̌덷��ANOVA�Ōv�Z���ꂽ�����a(SS#W)����ѕ��ϕ���(MS#W)�̌덷�����������Ȃ�
��F��ɂ��Ă����l�A�O���[�v�Ԃ̕��ϕ���(MS#B), MS#W�Ƃ��ɒ��������
21.21 ANCOVA Assumptions
��ANOVA�ł����Ƃ���̌덷��#ij�ɑΉ����AANCOVA�ł��l�������ׂ��덷��'#ij�����߂���
�E��ɂ���āANID�̑O��܂���i���K���A�����U���j
�E���K���A���U�َ̈����̌���ɂ́A�e�QJ�̊ϑ�����A����b#W�̎��ӂ̌덷�ł��邩���ׂ�
��ANCOVA�ɓ��L�̕t���I�ȑO��R��
�P�D�e�Q�̔w�i�ɂ����A�����͂Ƃ��ɕ��s�ł��邱��
�@�� ���̑O��ɔ�����ꍇ�ł��A�����U�ɂ�����邩������Ȃ����A�͂�����Ƃ������ʂ������Ȃ��\��������
�@�E�P�v���ł���A����قǐ[���ɂ͂Ȃ�Ȃ� (Glass et al., 1972)
�@�EJ�̉�A������������W�c����̂��̂��m���߂���@������(p.604�㔼�̌v�Z)
�@�@�� Figure 18.4�̗���������ꍇ�Ap.605�̍ŏI�I�ɋ��߂�ꂽF�l����A�O��P�̈ᔽ�͖Ƃ��iF = .62�ƒႢ�̂ŁA�L�ӂł͂Ȃ��j
�Q�D��A���Ƃ̂��Ă͂܂肪�悢����
�@�� ANCOVA��K�p���邠����P�[�X��X, Y�͐��`�W�����肳��Ă���
�@�E�����_�����o�����܂��������ƂŌ덷�͍ŏ�������A�W���덷�ɂ���Ă�����m���߂邱�Ƃ���
�@�E�ɂ���ẮA�Ȑ����ւ�`���W�����肤��
�� X, Y�ǂ��炩�ɐ��w�I�ϊ��������Ȃ����Ƃʼn���
�R�D�����U�͌Œ艻����Ă���A����덷���܂܂Ȃ�
�E���S�ɐM��������Ƃ͂����Ȃ������U���\�z�����̂ŁA��������߂Œ����ɂ�����덷�̎�ނ͍l������Ă���
�E����덷��X, Y�Ŋϑ�����鑊�ւɂ���Čy�������
21.12 ANCOVA Precautions
���������̐����iIQ�Ƃ��j���قȂ钆�ŁA�]���ϐ��̗L�ӂȈႢ��T��Ƃ��A�u���v��̕W�����v�������Ȃ��Ă���
�@�E�����_�����o���ꂽ�����ł́A�l���ɂ���Č���ɂ����邱�Ƃ� �����I�ł͂Ȃ��^�ł��Ȃ�����������
�@�E�ނ荇���̂Ƃꂽ�ϑ� (matching) ���A���������ł̐[���Ȗ��ƂȂ邱�Ƃ�����
�@�@�� ANCOVA��p���邱�Ƃɂ��A��菜�������v��X�ւ̕�����݂Ă���
���[���I�Ȋ��ł̒����ł́A�����_�����o������ĉ��߂�e�Ղɂ��邱�Ƃ��ł��Ȃ�
�@�EANCOVA�����ɓK�p�ł��Ă��A�{���Ɍ덷���Ȃ��Ɗm�M���邱�Ƃ͂ł��Ȃ�
�@�@�� ���o�����܂������Ȃ������Ƃ��̖h�q��i�ł͂Ȃ�
���ϑ��O���[�v�ԂŊS�Ƃ͈قȂ�v��X�����݂����ꍇ�AANCOVA�͍̂����ϗʂŐ���ł��邪�A�����ɂ�����Ȃ����������Ƃ�
�@��j�قȂ�Ώۊw�N��10�N���C13�N���ŕʌQ�̊ϑ��������Ȃ����Ƃ��A11.5�N���̊ϑ��Ɠ����Ƃ����邩�H
�������U�ɂ�鐄��́A���`�œ����̉�A���������Ȃ���A�덷�͑傫�Ȃ܂�
���v��X�ł̈Ⴂ�̕����傫���ƁA���G�������A���Œ������ꂤ�邽�߁A����I�ȉ��߂Ƃ͂����Ȃ��Ȃ萄�_���甭�W���Ȃ�
21.13 Covarying Versus Stratifying
�������U��treatment�i�ϑ��Q�Ԃ̏��u�̈Ⴂ�j�ǂ����D�悳���邩�ɂ���āA�f�U�C���╪�͕��@��ւ���̂��悢
�@�� �ȕւ�ANOVA�ɂ��邩�A����͂̍���ANCOVA�ɂ��邩
�������UX��K�̕������x�������݂���v���Ƃ��Ĉ������Ƃ��ł���
�@�E�����ɑ�����balanced design
�@�E�e�Q�Ń����_�����o�����A����͂����߂�
�@�@�� ANCOVA��p����D�܂����f�U�C��
�@�@�� �]���ϐ��Ƌ����U�̑��ւ�����͂ɊW����
�������_�������ꂽ�����ł͂Q�v����ANOVA�̕���ANCOVA���D�܂��
�@�E�L�v�Ȓlj����Ƃ��āAtreatment�𑼂̃��x���ɂ���ʉ����ĉ��߂ł���
�@�EX��Y�����`�̊W�ɂȂ��ꍇ�AANCOVA�̕��G�Ȓ������Ԃ��ĕs���ɂ͂��炭
21.14 Chapter Summary
�@�EANCOVA��ANOVA�Əd��A��g�ݍ��킹���悤�Ȍ���
�@�@�� ����͍���
�@�EX, Y�̑��ւ̍��������ߎ�ƂȂ�
�@�E�덷�̌y���Ɏg���邪�A���\�ł͂Ȃ�
�@�E�O��F�덷���Ɨ����A���K���z���A���ʂ������U�ɂ���
�@�@�� ����ɐ��`�̌X����`����A�������L���Ă��邱��
�@�@�� �����U�͌Œ���ʂ��܂�
�@�E�����_�����o�����Ȃ���AANOVA�Ƃ̒����Ŏg��������̂��悢
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����j
�f�B�X�J�b�V�������R�����g
�E�����U���́iANCOVA�j�͕��U����(ANOVA)�ł̌덷�����ɂ����镔��������ɕ������邱�Ƃɂ���āA���U���͂ł͂킩��Ȃ����Ƃ𖾂炩�ɂł���B
�E�������A�{���ł����x�����ӂ��Ă���悤�ɁA�f�[�^�̎�̂܂������J�o�[����ړI�Ŏg���ׂ��ł͂Ȃ��B���U���͂ł����ׂ�ꂻ���Ȍ����ۑ���킴�킴�����U���͂�p���Ă���_���́A�����f�U�C����f�[�^�̎�̉ߒ��ɖ�肪�Ȃ��������m���߂�ׂ��B
�E�����U���͂�p�����ꍇ�A���ϗʁicovariate�j�́A�]���ϐ��ƒ����̊W�ɂ���A�����ꂼ��̓Ɨ��ϐ��Ƃ̉�A�����̌X���������ł���i���s���Ă���j�ꍇ�Ɏg�p�ł���B����āA�g�p�ł��邩���s���̌��肪�K�v�ł���B�@�@�@�i����A�����j

�y�[�W�g�b�v�ɖ߂�
���ӌ���R�����g�������������܂������������B
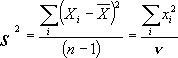 �@�́A�T���v����n�ł͂Ȃ�n-1�i���R�x�j��p���闝�R�́A��W�c�̕��U�ɋ߂��Ȃ�悤�ɂ��邽�߁B���ɃT���v����n���������� n �ŕ���2��̘a������̂� n-1�Ŋ���ƕ��U�����Ȃ�قȂ邱�ƂɂȂ�B�܂�n�Ŋ����Ă��܂��ƕ�W�c�̒l�̂�������������ς����Ă��܂����߂�n-1�Ŋ���B����䂦�ɁA���̕��U�̏o������s�Ε��U�iunbiased variance�Gthe variance of a population estimated from a sample�j�Ƃ��Ă���B�������A�l�����傫���Ȃ�Ȃ�قǁAn��n-1�̈Ⴂ�͔��X������̂ɂȂ�̂łǂ�����g���Ă����܂�ς��Ȃ��B�ꕪ�U�𐄒肷�邽�߂ɁA�ʏ�̓��v�\�t�g��n-1���g�p���Ă���B
�@�́A�T���v����n�ł͂Ȃ�n-1�i���R�x�j��p���闝�R�́A��W�c�̕��U�ɋ߂��Ȃ�悤�ɂ��邽�߁B���ɃT���v����n���������� n �ŕ���2��̘a������̂� n-1�Ŋ���ƕ��U�����Ȃ�قȂ邱�ƂɂȂ�B�܂�n�Ŋ����Ă��܂��ƕ�W�c�̒l�̂�������������ς����Ă��܂����߂�n-1�Ŋ���B����䂦�ɁA���̕��U�̏o������s�Ε��U�iunbiased variance�Gthe variance of a population estimated from a sample�j�Ƃ��Ă���B�������A�l�����傫���Ȃ�Ȃ�قǁAn��n-1�̈Ⴂ�͔��X������̂ɂȂ�̂łǂ�����g���Ă����܂�ς��Ȃ��B�ꕪ�U�𐄒肷�邽�߂ɁA�ʏ�̓��v�\�t�g��n-1���g�p���Ă���B