(1)数値積分
(a) 台形公式:微小な区間を直線で近似して積分
(b) シンプソンの公式:微小な区間を2次関数で近似して積分
(2)数値微分:微分係数からもとの関数の形を求める。
(a) オイラー法:微小な区間離れた点を始点の傾きで求める。
(b) ルンゲ・クッタ法:微小な区間離れた点を始点、中間点および終点の傾きを使って求める。
以下のプログラムに関数v_productを書き加えて、実行出力が「ベクトルaとbの外積は(1.00, -1.00, 1.00)です。」となるようにせよ。
#include <stdio.h>
typedef struct {double x; double y; double z;} Vector3;
///// ここに関数を書き加える /////
int main(void)
{
Vector3 a = {1.0, 1.0, 0}, b = {0, 1.0, 1.0}, c;
c = v_product(a, b);
printf("ベクトルaとbの外積は(%.2f, %.2f, %.2f)です。\n", c.x, c.y, c.z);
return (0);
}
以下の解説で例として示したsin(x)の0からπまでの積分を台形公式を使って求めるプログラムをもとに、sqrt(1-sin(x))の0からπまでの積分を求めるプログラムを作成せよ。
<出力例>
sqrt(1-sin(x)), [0, pi]積分:台形公式による解:1.656820
以下のプログラム中にコメントとして示している(1) sum1に0.1を10回加算、および(2) sum2がsum2<1.0の間sum2に0.1を加え続ける、の部分にその意味するところのコードを書き加えて、その通りにプログラムが動作するようにせよ。
#include <stdio.h>
int main(void)
{
double sum1 = 0.0, sum2 = 0.0;
printf("値0に2種類の方法で0.1を加算した結果を表示します。\n");
// (1) sum1に0.1を10回加算 //
printf("(1) 0.1を10回加算 : %.20f\n", sum1);
// (2) sum2がsum2<1.0の間sum2に0.1を加え続ける //
printf("(2) 1.0未満の間0.1を加算: %.20f\n", sum2);
return (0);
}
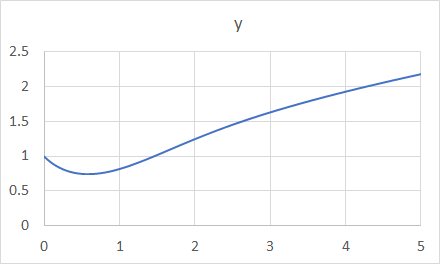
オイラー法の説明のところで示した微分方程式y=y'を解くプログラムを参考にして、微分方程式 y'+ y*y = xを区間[0, 5]の範囲で求めてCSVファイルに出力するプログラムを作成せよ。ただし、 x=0のときy=1とし、xの区間[0, 5]は100等分して、それぞれの点でのyの値(101点)を求めるとする。CSVファイルをExcelで開いて散布図としてグラフ化すると、次のようなグラフが描けるはずである。

「1」台形公式
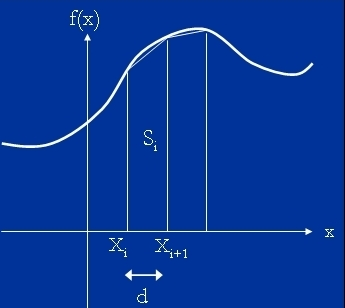
関数f (x)を数値積分するには、xを微小な区間に分割してそれぞれの区間での面積を求めて加算する。台形公式では、下図のように積分区間をn個の領域に等分割してそれぞれの区間を直線で補間して計算する。
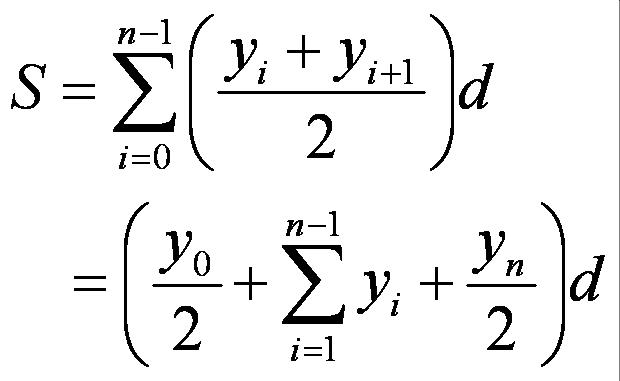
以下に、sin(x)の0からπまでの積分を台形公式を使って求めるプログラムを示す。
/* 台形公式によるsin(x)の積分 */
#include <stdio.h>
#include <math.h>
#define PI 3.141592653589793
#define N 100
int main(void)
{
double x0=0, x1=PI;
double dx, sum=0;
int i;
dx = (x1 - x0) / N;
sum = sin(x0)/2;
for (i=1; i<N; i++){
sum += sin(x0+dx*i);
}
sum += sin(x1)/2;
sum *= dx;
printf("台形公式による解:%f\n", sum);
printf("解析的に求めた解:%f\n", -cos(x1)+cos(x0));
return (0);
}
「2」シンプソンの公式
シンプソンの公式では、積分区間をn個(n: 偶数)の領域に等分割してそれぞれの区間を2次曲線で補間して計算する。
下図のようにある2つの区間の面積をSiとすると、これは以下のように計算できる。
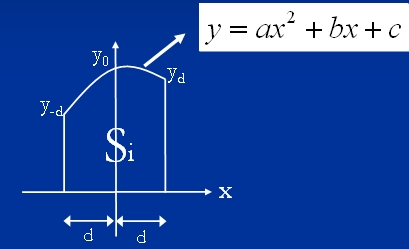
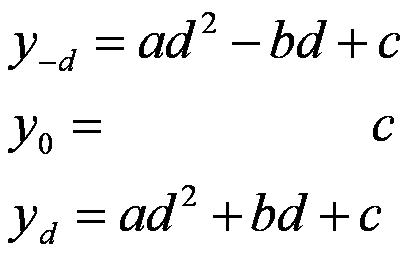
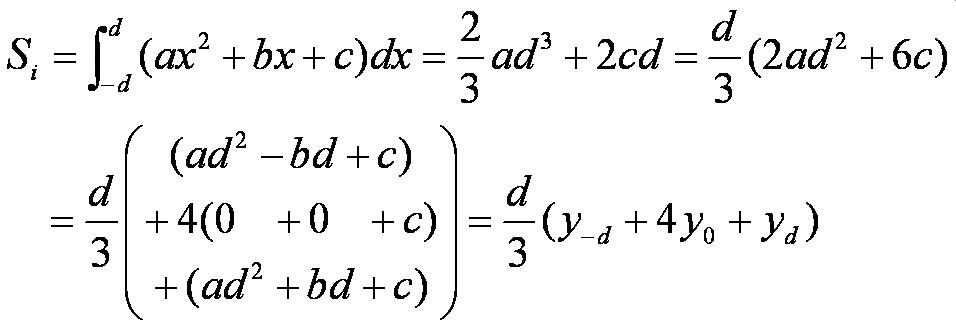
この全区間の和を求めると積分値が計算できる。
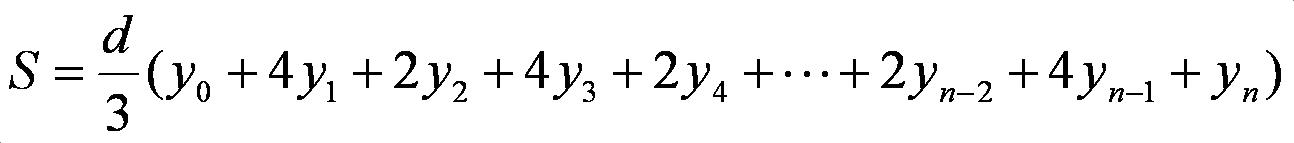
以下に、sin(x)の0からπまでの積分をシンプソンの公式を使って求めるプログラムを示す。台形公式の場合小数点以下4桁目ぐらいから解析的な解との違いが出ているが、シンプソンの公式を用いるとそれよりはるかに正確に計算できる。
/* シンプソンの公式によるsin(x)の積分 */
#include <stdio.h>
#include <math.h>
#define PI 3.141592653589793
#define N 100
int main(void)
{
double x0=0, x1=PI;
double dx, sum=0;
int i;
dx = (x1 - x0) / N;
sum = sin(x0);
for (i=1; i<N; i+=2){
sum += 4*sin(x0+dx*i) + 2*sin(x0+dx*(i+1));
}
sum -= sin(x1);
sum *= dx/3;
printf("シンプソンの公式による解: %f\n", sum);
printf("解析的に求めた解 : %f\n", -cos(x1)+cos(x0));
return (0);
}
数値計算で微分方程式を解くということについて
微分方程式では、ある点での微分係数、つまり傾きが与えられている方程式である。この傾きをもとに次の点を計算で求めていくことが、数値計算による微分方程式の解法となる。ここでは、そのうち代表的な2つの方法、オイラー法とルンゲクッタ法について学習する。
「3」オイラー法による微分方程式の解法
ここでは、y'=yという微分方程式を扱う。(この式は解析的に簡単に解けて、解はy=a*exp(x)となる。ここでaは任意定数である。)
x=X0のときy=Y0という初期条件において、区間
[X0, X1]での解を、この区間
をN等分して求めることを考える。
オイラー法では、下図のようにxが微小な値hだけ増加したときのyの増分を初期値での傾きy'で直線的に増加していくものとして計算を行う。
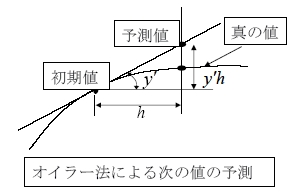
つまり、![]() を全ての微小区間に適用してyの値を決めていく。
を全ての微小区間に適用してyの値を決めていく。
この計算を行うプログラム例を以下に示す。ここでは、y' = f(x, y) = yとして関数f(x, y)を作成している。また、X0=0, Y0=1を初期条件として、X1=2までの解を求めている。同時に解析的な解y=exp(x)も計算して、計算結果をeuler1.csvというファイルにテキストファイルとして保存するようになっている。このファイルをExcelなどの表計算ソフトウェアに読み込めば、グラフ表示させることができる。
/* オイラー法によるy=y' の解 */
#include <stdio.h>
#include <math.h>
#define N 100 // 分割数
#define X0 0.0 // 初期条件
#define Y0 1.0 // 初期条件
#define X1 2.0 // ここまで計算
#define FILENAME "euler.csv" // 保存ファイル名
double f(double x, double y)
{ // この関数では引数xを使っていないので警告が出る
return (y);
}
int main(void)
{
double x, y, h;
int i;
FILE *fp;
h=(X1-X0)/N;
x=X0; y=Y0;
fp = fopen(FILENAME, "w");
fprintf(fp, "x, Euler-y, exp(x)\n");
fprintf(fp, "%3.2f, %3.5f, %3.5f\n",x, y, exp(x));
/* オイラー法にかかわる部分は以下のforループ内の最初の2行のみである */
for (i=1; i<=N; i++) {
y += f(x, y)*h;
x += h;
fprintf(fp, "%3.2f, %3.5f, %3.5f\n",x ,y, exp(x));
}
fclose(fp);
printf("結果を%sに書き込みました。\n", FILENAME);
return 0;
}
「4」 ルンゲ-クッタ法による微分方程式の解法
オイラー法では、ある区間の始点における傾きで終点のyの値を予測していた。それに対して、ルンゲ-クッタ法では、始点、終点及び中間点の傾きを用いて終点のyの値を予測する。それだけ精度よく関数の近似値を求めることが可能である。
前と同じy' = yという微分方程式を扱う。(この式は解析的に簡単に解けて、解はy=a*exp(x)となる。ここでaは任意定数である。)
ルンゲ-クッタ法では、1つの区間のyの増分を以下のようにして決める。ここではなぜこのように重みをつけて計算するのかという理由は取り扱わないが、このようにすることによりオイラー法と比較してはるかに精度の高い計算が可能となる。
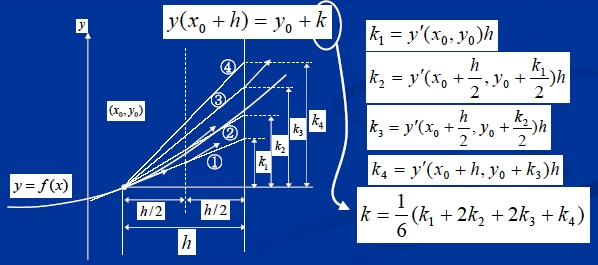
これをy' = f(x, y)という微分方程式に適用すると、この部分は以下のようなプログラムで表現できる。ここでは初期条件を(X0, Y0), 求める区間を[X0, X1]としている。
h = (X1-X0)/N;
x = X0;
y = Y0;
printf(“%f, %f\n” x, y);
for (i=1; i<=N; i++){
k1 = f(x, y)*h;
k2 = f(x+h/2.0, y+k1/2.0)*h;
k3 = f(x+h/2.0, y+k2/2.0)*h;
k4 = f(x+h, y+k3)*h;
y += (k1+2*k2+2*k3+k4)/6.0;
x = x + h;
printf(“%f, %f\n” x, y);
}
以下に、「3」で示したプログラムをルンゲ-クッタ法を用いるように変更したプログラムを示す。
/* ルンゲ・クッタ法によるy=y' の解 */
#include <stdio.h>
#include <math.h>
#define N 100 // 分割数
#define X0 0.0 // 初期条件
#define Y0 1.0 // 初期条件
#define X1 2.0 // ここまで計算
#define FILENAME "runge.csv" // 保存ファイル名
double f(double x, double y)
{ // この関数では引数xを使っていないので警告が出る
return (y);
}
int main(void)
{
double x, y, h;
double k1, k2, k3, k4;
int i;
FILE *fp;
h=(X1-X0)/N;
x=X0; y=Y0;
fp = fopen(FILENAME, "w");
fprintf(fp, "x, Runge-y, exp(x)\n");
fprintf(fp, "%3.2f, %3.5f, %3.5f\n",x, y, exp(x));
for (i=1; i<=N; i++) {
k1 = f(x, y)*h;
k2 = f(x+h/2.0, y+k1/2.0)*h;
k3 = f(x+h/2.0, y+k2/2.0)*h;
k4 = f(x+h, y+k3)*h;
y += (k1+2*k2+2*k3+k4)/6.0;
x += h;
fprintf(fp, "%3.2f, %3.5f, %3.5f\n",x ,y, exp(x));
}
fclose(fp);
printf("結果を%sに書き込みました。\n", FILENAME);
return 0;
}
標準偏差1の正規分布(ガウス分布)の-X <=x<=Xの積分値S(X)の値を返す関数を、シンプソンの公式を用いて半分の区間[0, X]を100等分して計算した結果を2倍した値を返すように作成する。その関数を用いて、Xの値を0.2から3.0まで0.2間隔で計算して以下に示す例の通りに出力するプログラムを作成せよ。被積分関数は正規分布曲線だからX=1.0のとき0.682...とならなければならない。またπは#define PI 3.141592653589793として用いること。
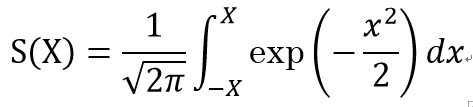
実行結果出力
標準偏差1のガウス分布の積分:区間[-X, X] X 積分値 0.2 0.158519 0.4 0.310843 0.6 0.451494 0.8 0.576289 1.0 0.682689 1.2 0.769861 1.4 0.838487 1.6 0.890401 1.8 0.928139 2.0 0.954500 2.2 0.972193 2.4 0.983605 2.6 0.990678 2.8 0.994890 3.0 0.997300
実習課題4で行った微分方程式 y'+ y*y = xをオイラー法で解くプログラムを、区間や初期条件はそのままでルンゲ・クッタ法を用いた方法に書き換えよ。
N×N行列の転置行列を求める関数
void transpose(double ma[ ][N]);
を作成し、 以下のように宣言した4×4行列の転置行列を求めるプログラムを作成せよ。
#define N 4
#define A {{1,3, 4,7}, {2,5,7,8}, {1, 3,6,9}, {5, 2, 4, 6}}
double ma[][N] = A;
ここではN = 4であるが、関数自体はNが任意の自然数であっても機能するように作成すること。プログラムを実行したときの出力は以下のとおりにすること。
-----------------------
*** もとの行列 ***
1.00 3.00 4.00 7.00
2.00 5.00 7.00 8.00
1.00 3.00 6.00 9.00
5.00 2.00 4.00 6.00
*** 転置した行列 ***
1.00 2.00 1.00 5.00
3.00 5.00 3.00 2.00
4.00 7.00 6.00 4.00
7.00 8.00 9.00 6.00
------------------------
==お疲れさまでした。この授業はこれで終了です。あとは期末課題に取り組んで下さい。======