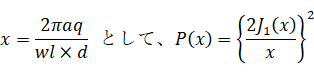
期末課題 （次のA～DのソースプログラムをTeamsの課題の該当する場所に提出）

期末課題A（ファイル名pfA.cとして提出すること）　

日本人の平均寿命は、男性が81.09歳、女性が87.14歳です（2023年度、厚生労働省、自国に合わせて変更可）。この値に365日を掛けた値を四捨五入したものを平均寿命日数とします。また、西暦（グレゴリオ暦）で表した年をyearとして、その年がうるう年（2月が29日で1年が366日の年）であるのは、(a) yearが4で割り切れ、かつyearは100で割り切れない年、または(b) yearが400で割り切れる年、となります。以上を踏まえて、誕生日を西暦で入力して今日まで生きた日数と平均余命日数を以下の通りに出力するプログラムを作成せよ。ただし、平均よりもm日長生きしていた場合には、「あなたは平均よりm日長生きしています。」と出力すること。また、誕生した年は前年以前と仮定して良い（条件分けが複雑になるので同じ年の場合を除きます）。
======= 出力例 ===================
これまで生きてきた日数と平均余命日数を計算致します。
男性ならばM(m), 女性ならばF(f)を入力してください：M
生年月日を西暦で入力してください（去年以前）。
年：2000
月：1
日：1
ご苦労様。あなたは今日まで9109日生きてきました。
あなたの平均余命はあと20489日です。
==================================
（ヒント）誕生日をy0年m0月d0日、現在の日付をy年m月d日とする。現在の日付は9回目の解説を参考にtime( )関数で取得すること。y0 >= yならば適当なメッセージを表示して終了する。月に含まれる日数は、
int month_day[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
のような配列を作成して参照すればよい。ここではインデックスが月そのものを示すようにしている。うるう年かどうかの判断は、

int leap_year(int year)
{
    if (((year%4==0) && (year%100!=0)) || (year%400==0)) return 1;
    return 0;
}
のような関数を作成して利用すると良い。

期末課題B（ファイル名pfB.cとして提出すること）

半径a(μm)の円形開口に垂直に波長wl(μm)のコヒーレントな平行光が入射した場合のフラウンホーファー回折光を開口からd(mm)離れたスクリーン上で観察する。回折光中央の極大点の強度を1として、その位置から距離q(mm)離れたスクリーン上の点の強度をPとすると、

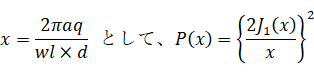
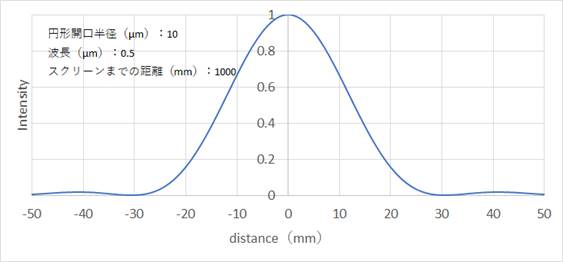
と表すことができる。ここで、J1(x)は5回目の演習課題５Cで作成した1次の第1種ベッセル関数であり、x = 0のときP(0) = 1である。キーボードから半径、波長、スクリーンまでの距離を入力してスクリーン上の回折光の強度Pをq = -50 (mm)から50 (mm)まで1 mm間隔でCSVファイル(airy_pattern.csv)に以下の表示例の通りに出力するプログラムを作成して提出せよ。また、CSVファイルをExcelで開いて散布図としてグラフ表示した下図のようなグラフの画像ファイルを提出せよ。
====== 出力例 ==================
円形開口からのフラウンホーファー回折を計算します。
計算範囲：スクリーン上；-50 mm～50 mm
円形開口半径（μm）：10
波長（μm）：0.5
スクリーンまでの距離（mm）：1000
＜結果をairy_pattern.csvに保存しました＞
====== airy_pattern.csvをテキストエディタで開いたときの内容 ====
q(mm), Intensity
-50.0, 0.004570
-49.0, 0.006225
…. （途中省略）…
50.0, 0.004570
=====================================================
ExcelでCSVファイルを読み込んで散布図としてグラフ表示して軸ラベルと説明文を加えた図


＝＝＝＝＝＝


期末課題C（ファイル名pfC.cとして提出すること）

2次方程式a*x*x + b*x + c=0の係数a, b, cをdouble型の引数として受け取り、その解をdouble型の配列の引数solution[2]に値を設定して返す関数を作成して下さい。関数の返り値は２つの実数解のとき2、重解のとき1、a=0で2次方程式でないとき0、複素数解のとき－１の整数とします。また、この関数を用いて任意の2次方程式の解を求めるプログラムを作成して下さい。ただし、解を表す配列の２つの要素は、２つの実数解のときはその２つの解を表し、重解のときは２つとも同じ解を表し、複素数解の時は解p±iqのpとqを表すものとします。また、計算出力後にもう一度繰り返すかの問いを以下の実行例のように表示し、yを入力すると処理を繰り返すものとします。以下のソースコード（一部のみ表示）と実行例を参考にして下さい。

#include <stdio.h>
#include <math.h>
int quadratic(double a, double b, double c, double sol[])
{
    double D;
    
    if (a == 0) return 0; //2次方程式でない
    
    D = b * b - 4 * a * c;
    
    if (D == 0) {
        sol[0] = sol[1] = -b / (2 * a);
        return (1); //重解
    } else if (D >= 0) {
        /*********/
        return (2); //２つの実数解
    } else {
        /*********/
        return (-1); //複素数解
    }
}
int main(void)
{
    /*********/
    
    return (0);
}

＜===== 実行例 ==========＞
2次方程式a*x*x + b*x + c=0の解を計算します。
a = 1.0
b = 2.0
c = 2.0
複素数解：1.00 ± i1.00
もう一度実行する場合yを入力：y
a = 1.0
b = -3.0
c = 2.0
２つの実数解：1.00, 2.00
もう一度実行する場合yを入力：q
=============================

期末課題D（ファイル名pfD.cとして提出すること）

#define PI 3.141592653589793
とします。y = (4/PI)*(sin(x) + sin(3*x)/3 + sin(5*x)/5 + sin(7*x)/7) + ... + sin((2*n-1)*x)/(2*n-1)) + ... は、矩形波（周期: 2π、y = -1: -π<= x < 0, y = 1: 0 <= x < π）のフーリエ級数であり、n項目までの和の値はnが大きくなるほどもとの矩形波に近づきます。nをキーボードから入力し、その項までのフーリエ級数をx = -5からx = 5までxの間隔0.1で計算してxとyの値をCSVファイルにファイル名square_wave.csvとして保存するプログラムを作成して下さい。ファイルのフォーマットは9回目の演習問題９Bと同様にExcelで開いてグラフ化できるようにして下さい。
====== 実行例 ===========

矩形波(y = -1: -π<= x < 0, y = 1: 0 <= x < π）のフーリエ級数の計算
何項目までの和を計算しますか：4
x = -5からx = 5まで、4項目までのフーリエ級数をsquare_wave.csvに保存しました。
====== square_wave.csvの内容（n=4の場合）======
x, y
-5.000000, 1.056535
-4.900000, 0.996215
.... （途中省略）...
4.900000, -0.996215
5.000000, -1.056535

==========　以上　==========