今回は時間に依存した現象を取り上げて、視覚化の代表格でもある「アニメーション」について学びます。まず最初に準備として、アニメーションに関連したMathematicaのコマンドを紹介します。

Manipulateはパラメータを含む関数をプロットしたときに、各パラメータの値に対しての図を作ってくれるコマンドです。さらにそのパラメータをマウス操作により動かすことができます。以下のように、Sin[a*x]という関数に対して早速試してみましょう。

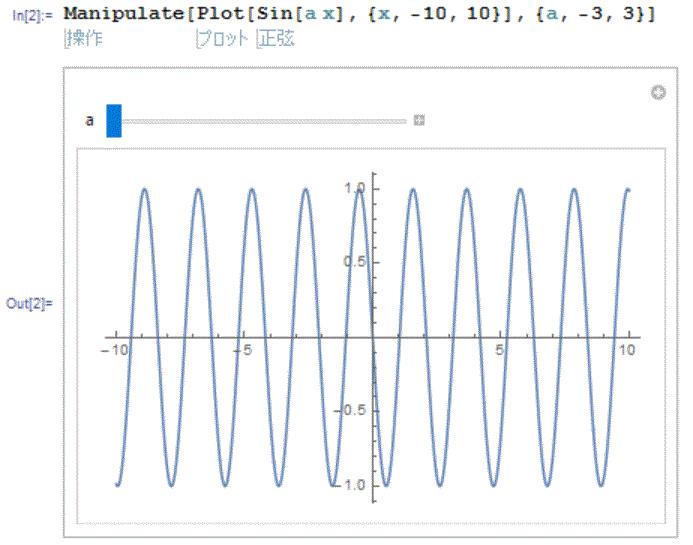
出てきた図に現れたつまみをマウスで動かして見てください。aの値が変えられるはずです。

練習問題:以下を試してみましょう。

• Manipulate[ Plot[a x + b, {x, -3, 3}, PlotRange -> {-5, 5}], {a, 0, 10}, {b, -1, 1}]
• Manipulate[ Plot3D[Cos[x*(y - a)/2], {x, -3, 3}, {y, -3, 3}], {a, -3, 3}]
• いろいろ試してみましょう。

Manipulateは出てきたつまみを自分で動かさなければいけません。 自動的に動かしてアニメーションにするには、Animateというコマンドを使います。

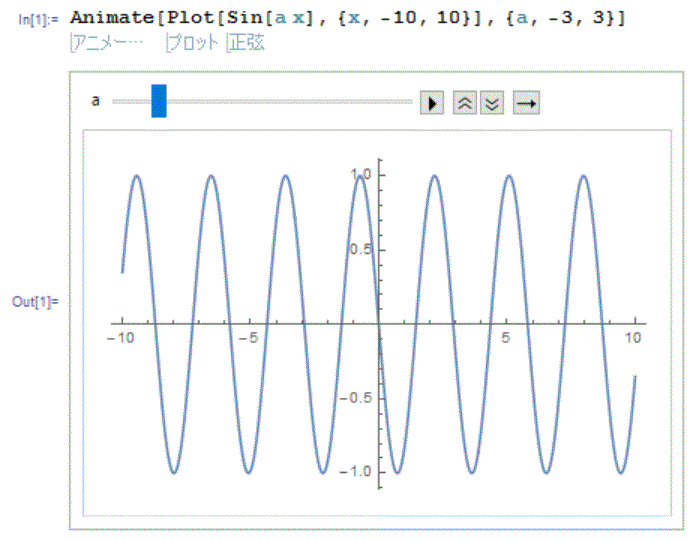
このHP上の図としては上のManipulateと同じですが、皆さんのMathematicaの画面上では自動的に動いているはずです。このように、Mathematicaでは簡単にアニメーションを作ることができます。

• Animate[ Plot[Sin[x + b], {x, -3, 3}], {b, -3, 3}]
• Animate[ContourPlot[x^2 + y^2 - a, {x, -1, 1}, {y, -1, 1}, Contours -> {0, -0.4, 0, 4}], {a, 0, 2}]
• いろいろ試してみましょう。

• {1,2,3,4,5}+10
• z={3, 5, 7}; z-3
• r={x,x^2,x^3}; Plot[r, {x, -1, 1}]
• w={1,2,3,4,5}; と定義してから以下を試しましょう。
• First[w]（最初を取り出す）
• Last[w]（最後を取り出す）
• Part[w,4] （Part[w,i]はi番目を取り出すという意味）
• Take[w,{2,5,2}] (Take[w,{i,j,s}]はwのi番目からj番目までの要素をs番飛びに取り出すという意味)
• Delete[w,3] (Delete[w,i]はi番目を取り除くという意味)
• Insert[w, 2.5, 3] （Insert[w, x, i]はwのi番目にxを挿入するという意味）
• Join[w,{6,7,8},{9,10,11}]（いくつかのリストを組み合わせる）

• 正弦波と余弦波
  Manipulate[Plot[{Sin[t - x], Cos[t - x]}, {x, 0, 20}], {t, 0, 10}]
• 振動数の異なる正弦波
  Manipulate[Plot[{Sin[2t - x],Sin[t-x]}, {x, 0, 20}], {t, 0, 10}]
• 波数の異なる正弦波
  Manipulate[Plot[{Sin[t - 2x],Sin[t - x]}, {x, 0, 20}], {t, 0, 10}]
• 波数も振動数も異なるが、速度が等しい正弦波
  Manipulate[Plot[{Sin[t - 2 x], Sin[t/2 - x]}, {x, 0, 20}], {t, 0, 10}]
• 波の重ね合わせ・干渉
  Wave[t_, x_] := Sum[Sin[n t - x], {n, 0, 4}];
  Manipulate[Plot[{Wave[t, x]}, {x, 0, 20}, PlotRange -> {{0, 20}, {-5, 5}}], {t, 0, 10}]
• ManipulateやAnimateではいくつかの変数を動かすこともできます。
  Manipulate[ Plot[a x^2 + b x + c, {x, -10, 10}, PlotRange -> {{-10, 10}, {20, -20}}], {a, -10, 10}, {b, -10, 10}, {c, -10, 10}]
• Animate[Plot[Sin[a x] + Sin[b x], {x, 0, 10}, PlotRange -> {{0,10},{-2,2}}], {a, 1, 5}, {b, 1, 5}, AnimationRunning -> False]
  （最後のオプションは自動的にアニメーションが始まらないようにするものです）
• 放物運動の軌跡
  v = 10; g = 9.8; a = Pi/3;
  Animate[ParametricPlot[{v Cos[a] t, v Sin[a] t - g t^2/2 }, {t, 0, n}, PlotRange -> {{0, 9}, {0, 4.5}}], {n, 0.1, 1.8, 0.05}]
  （最後の{n, 0.1, 1.8, 0.05}はnを0.1から1.8まで0.05間隔で増やしていくという意味）
• 三次元的空間の放物運動も同様にプロットできるでしょうか？
• ドーナツづくり
  Manipulate[ ParametricPlot3D[{{(Sin[a] + t) Cos[b], ( Sin[a] + t) Sin[b], Cos[a]}}, {a, 0, 2 Pi}, {b, 0, 2 Pi}], {t, 0.1, 2}]
• 穴が二つのドーナツは作れるでしょうか？
  （これは非常に難しい問題で担当教員も答えを知りません。時間がかかるのでテキストの次のページが終わってから挑戦してみてください。もしできたら教えて下さい）