名辞論理とヴェン図
――オイラーの場合――
橋本康二
一 はじめに
現代の大学の初等論理学の授業で名辞論理が教えられることはほとんどないと思われるが、分析哲学の入門授業では、ゴットロープ・フレーゲによる論理学革命を説明するために必要になるので、名辞論理が簡単に紹介されることも多く、そのときに必ずと言って良いほど持ち出されるのがヴェン図である(1)。ヴェン図をめぐる哲学的考察を行う連続研究の第二論文である本論文では、この名辞論理の解説で使われるヴェン図を取りあげる(2)。
まず、第二節では、紀元前四世紀にアリストテレスが研究を始めた名辞論理が、二十一世紀の現在、どのようなものであると一般に考えられているのかを、簡単に見ておく。次に、第三節では、十八世紀にレオンハルト・オイラー(一七〇七―一七八三)が名辞論理を解説するために考案した図形を検討する。この図形は、我々が集合演算のときに考えたヴェン図と同じ特徴(3)を基本的に持っており、それゆえ、自然な仕方で理解されることができるようになっている、と我々は論じることになる。しかし、第四節では、オイラーの図形には文字の使用が本質的に含まれており、その点で図形としての性格が弱くなっている、ということを我々は論じる。最後の第五節では、オイラーの図形では空集合が表示され得ないのではないかという指摘に対して、第四節での文字の使用という特徴を踏まえて、そうではなく、空集合は問題なく表示できるのだと反論する。
オイラーの図形は、十九世紀になってジョン・ヴェン(一八三四―一九二三)によって改良され(4)、さらにチャールズ・サンダース・パース(一八三九―一九一四)によって追加の改良が加えられた(5)。名辞論理とヴェン図の関係をより完全に論じるためには、彼らの改良版についても検討しなければならないが、それは別の論文で行う予定であり、ここでは、オイラーの図形に限定して考察する。
二 伝統的名辞論理学と現代述語論理学
古代ギリシア以来、西洋世界を支配してきた伝統的な論理学は、創始者の名前にちなんで「アリストテレス論理学」と呼ばれるが、「動物」、「人間」、「必滅」などの、「名辞」と呼ばれる語を基礎にして展開されるため、「名辞論理学」とも呼ばれている。名辞が二つ結合することで、基本的な文(命題)が形成される(6)。現在ならこれは「原子命題」とでも呼ぶべきなのだが、伝統的には「定言命題」と呼ばれている(7)。そして、この定言命題が組み合わされることで、三段論法という論証が構成される。したがって、この論理学はまた「三段論法論理学」とも呼ばれている。論理学であるから、名辞論理学の主要部分はこの三段論法を展開したところにあるのだが、この論文での我々の関心はその前段階である定言命題にあるので、三段論法の詳細にはここでは触れず、定言命題についてだけ、すこし詳しく見ておきたい。
名辞が二つ結合することで命題が形成されるが、単純に二つの名辞を並べるのではなく、「繋辞」とよばれる語で結び付けられることで命題は形成される。ただしこの結びつけ方には二種類があり、それらは互いに質が違うと言われる。一方の質は「肯定」、他方の質は「否定」と呼ばれ、前者は「(・・・は・・・)である」という語が担い、後者は「(・・・は・・・)でない」という語が担う。結び付けられた二つの名辞のうち、先に位置する名辞は「主語」、後に位置する名辞は「述語」と呼ばれる。主語と述語が肯定的に結び付けられてできた命題は「肯定命題」、否定的に結び付けられてできた命題は「否定命題」と呼ばれる。しかし、これだけではまだ命題としては完成していない。命題はその主語の量が二種類の仕方で限定されなければならない。一方の量限定は「全称」、他方の量限定は「特称」と呼ばれ、前者は「すべての」という語が担い、後者は「ある」という語が担う。主語が全称的に量限定された命題は「全称命題」、特称的に量限定された命題は「特称命題」と呼ばれる。かくして、二つの名辞からなる命題は、肯定命題か否定命題のどちらかであり、かつ、全称命題か特称命題のどちらかであるから、組み合わせると、全称肯定命題、全称否定命題、特称肯定命題、特称否定命題のちょうど四種類の命題が存在することになる。今、主語も述語も特定せずに、それぞれ「A」、「B」という図式で表すと、四種類の命題は以下のようになる。
(全称肯定命題) すべてのAはBである。
(全称否定命題) すべてのAはBでない。
(特称肯定命題) あるAはBである。
(特称否定命題) あるAはBでない。
なお、これらは順に「A命題」、「E命題」、「I命題」、「O命題」とも呼ばれている(8)。
四種類の命題は、それぞれ何を意味するのだろうか。ここでは、現代において一般にこれらの命題の意味がどう理解されているのかを見ておきたい。アリストテレスにさかのぼって、彼がどう考えていたのかをここで検討することは、残念ながら断念せざるを得ない。アリストテレス哲学の解釈の問題は、現在でも進行中であり、専門家でもないものが簡単に何かを述べることはできないからである(9)。しかし、次のように言われるかもしれない。すなわち、「アリストテレスの論理学は彼が意図した通りの意味論を持つのであり、それ以外の意味など持ちようがない。これはどんな論理学の体系についても言えることであり、そこに完備されている構文論と意味論以外のものを第三者が勝手に導入することはできないはずだ」と言われるかもしれない。これはその通りである。だが、どんな論理学の体系であれ、それは我々が実際に用いている言語をモデルにしたものであり、それに数学的に整備された構文論と意味論を与える試みであると見なすことができる。例えば、A命題のひとつである「すべての人間は必滅である」は、アリストテレスの体系の中では、彼が考えていた意味しか持たない。しかし、これはそのまま我々の日常的な言語の文そのものであると見なすことができ、アリストテレスの考えを度外視して、我々自身はこの文をどういう意味で使っているのだろうかと問うことができる。我々はこの文の意味を十分に理解しているのだが、例えば、幼い子供に教えるといった教育の現場などでは、その意味の説明に困難を感じることもあるだろう。この説明を可能な限り平易に行いたい、というのがこの論文で問題にしていることなのである。その際、アリストテレスに教えを請いたいところであるが、上述のような解釈の問題があるので、それはここでは断念せざるを得ない。しかし、幸いなことに、現代の我々には、フレーゲらによってもたらされた述語論理学の体系がある。これを参考にして、アリストテレスが取り上げた四種類の命題の、日常言語での意味を考えていきたい。
現代の述語論理学は、定言命題の名辞は性質を表しているとみなし、個物がこの性質を持っているか否かを考えることを基本にして、四種類の定言命題を以下のように分析する。
(全称肯定命題) すべてのxに関して、xがAならば、xはBである。
(全称否定命題) すべてのxに関して、xがAならば、xはBではない。
(特称肯定命題) あるxに関して、xはAであり、かつ、xはBである。
(特称否定命題) あるxに関して、xはAであり、かつ、xはBではない。
ここで「x」は個物を表し、それがある性質を持つことを「xはAである」などと表記している。このような分析は、たいていの論理学の入門書には書いてあることである(10)。そして、この分析は、おそらく我々の直観的理解を正しく言い表したものでもあるだろう。しかし、これで四種類の命題の意味が明瞭になったのかといえば、それは別の問題である。量化子や真理関数結合子の意味に馴染んでいる者にとっては、この説明で透明な理解が得られるであろう。しかし、すべての人にそれを期待することはできない。そうした人々にどうやって四種類の命題の意味を説明すればよいのであろうか。そこで出てくるのがヴェン図である。
三 オイラーのヴェン図の意味(11)
現代論理学による名辞論理学の四種類の命題の分析の基礎にあるのは、任意の性質と任意の個物が与えられると、その個物はその性質を持つか持たないかのどちらかである、という考え方である。この考え方に基づいて名辞論理学の四種類の命題の意味を理解することは、きわめて自然な考え方なので、おそらく、かなり昔から行われてきたことだと思われる。それを明確な意味を持った厳密な記号で示してみせたのが、フレーゲ以降の述語論理学である。しかし、これは厳密であるが、分かりやすさという教育的配慮はなされていない。他方、別の流れもあって、そこではこの四種類の命題の自然な理解を図形を使ってわかりやすく表示しようとすることが試みられてきた。それがヴェン図の研究として、今日まで続いているのである(12)。ヴェン図を最初に考案したのが誰なのかは分からないが(13)、出版された書物でヴェン図を世間に広めたのはオイラーである。この節では、オイラーのヴェン図の特徴を検討する。
オイラーは、ベルリン・アカデミーで研究活動に従事していたとき、ブランデンブルク=シュヴェート辺境伯であるフリードリヒ・ハインリヒから、娘のフリーデリーケ・シャルロッテ(一七四五―一八〇八)の教育を頼まれる。最初は対面で授業を行っていたようだが、何らかの事情によりそれが続行できなくなり、代わりに、手紙による遠隔授業を行うようになった(14)。その手紙が、後に(二人とも存命中に)、『自然学と哲学のさまざまな問題について、ドイツのプリンセスへおくった手紙』という題名の三巻本にまとめられて出版された(15)。この本に収められた、一七六一年二月一四日の日付がある第一〇二回目の手紙に初めてヴェン図が現れる(16)。このとき、オイラーは五四歳、フリーデリーケ・シャルロッテは十五歳である(17)。円熟期の大数学者が少女に論理学を分かりやすく説明するためにヴェン図を持ち出したのである。オイラーは、ヴェン図によって、名辞論理の考察が容易になり、論理学がまとっている神秘のヴェールが取り払われる、とまで述べている(18)。
オイラーは、性質が個物によって所有されることに着目して、ある性質を所有している個物のすべてを収容している一個の図形によって、当の概念を表すことができると考える(19)。この考えに基づいて、名辞論理の全称肯定命題は図1によって、全称否定命題は図2によって、特称肯定命題は図3によって、特称否定命題は図4によって、表されることになる(20)。
これらの図はいかにして四種類の命題が言わんとすることを子供にも分かるように伝えているのだろうか。
図1で考えてみよう。まず、オイラーのヴェン図では、文字「A」が付された円(以下、「円A」と呼ぶことにする)は性質Aを有する個物の集合を名指し、文字「B」が付された円(以下、「円B」と呼ぶことにする)は性質Bを有する個物の集合を名指している、と規約されているとしよう。全称肯定命題「すべてのAはBである」が主張しているのは、「すべてのxに関して、xがAならば、xはBである」と分析されたが、これは結局、性質Aを有する個物の集合は性質Bを有する個物の集合の部分集合である、ということを意味している。しかし、図1は、先のように円の指示対象を規約されただけでは、このことを意味することはできない。それちょうど、我々の通常の言語において、次の文字列が全称肯定命題を意味できないのと同じである。
性質Aを有する個物の集合 性質Bを有する個物の集合
我々の言語で全称肯定命題を意味させるには、「・・・は・・・の部分集合である」という述語を用意して、それと結合させて、次の文を形成しなければならない。
性質Aを有する個物の集合は性質Bを有する個物の集合の部分集合である。
これと類比的に、オイラーのヴェン図では、述語を導入する代わりに、円と円の間に一定の位置関係を取らせることによって、我々の通常の言語の文に相当するものを形成していると考えることができるであろう。すなわち、図1は、円Aが円Bの内部に配置されることによって、単なる単語の羅列ではない、日常言語の文に相当するものになっていると考えられるのである。しかし、このように解された図1が全称肯定命題を意味するのかというと、その必然性はまったくない。円の意味に関する規約だけを教えられている人は、図1を見て、それを全称肯定命題でなく、全称否定命題や特称肯定命題ないし特称否定命題を意味すると理解しても構わないし、そもそも何も意味していないと考えても構わない。「・・・は・・・の部分集合である」という述語の意味が純粋に規約で決められているように、内部にあるという位置関係が部分集合関係を意味するということも純粋に規約の問題にすぎない。そうすると、図1を見せられた人は、円が何を意味するのかという規約と、円の位置関係が何を意味するのかという規約を知っていなければならない。では、これらの規約を知っている人は、全称肯定命題が意味することは実は図1の意味することと同じだと言われて、全称肯定命題の意味を把握することができるだろうか。この場合、この人は確かに、全称肯定命題の意味は「性質Aを有する個物の集合は性質Bを有する個物の集合の部分集合である」という文の意味と同じであるということを理解できるようになる。この文が全称肯定命題「すべてのAはBである」よりも理解が容易であるとはおよそ考えられないが、そういうこともあるかもしれない。だとすると、この人は、全称肯定命題の意味を最終的に把握できたことになる。しかし、そうだとすれば、最初から、図1ではなく、文「性質Aを有する個物の集合は性質Bを有する個物の集合の部分集合である」という日常言語の文を示せば十分だったのである。ここでは、ヴェン図は、理解を容易にするという教育的目標をまったく遂げておらず、それを使うことに何の意味もないのである。
ヴェン図が教育手段として有用であるためには、その意味は別の方法で与えられていると考えなければならない。そこで提案したいのが、第一論文で集合演算で使われるヴェン図を解釈したときに用いた方法である(21)。それによると、ヴェン図の各々の図形は最小部分から構成されており、おのおのの最小部分は個物の名前であり(同じ個物が二つの名前を持つことはない、すなわち、同じ個物が二つの異なる最小部分から名指されることはないとする)、当の図形は各々の最小部分が名指す個物すべてを要素としてもつ集合の名前である。このヴェン図解釈の基礎になっている考えは、物の集まりである集合という抽象的対象を視覚的に表そうという考えである。例えば、人間の集合を考えてみよう。各々の人間は空間的に離れて存在するので、そのすべてを見ることはできない。どこか地球上の一箇所に集めることができれば、すべての人間を見渡すことは可能かもしれないが、それは現実問題としてできない。しかし、ひとりひとりの絵を描き、それらを集めて、人がみな一箇所に集まっている絵を描くことはできる。それが人間の集合の絵であり、それは人間の集合を視覚的に表現したものである。これを一般化したものが、ここで解釈されているヴェン図なのである。
以上のヴェン図解釈に基づいた場合、ヴェン図による名辞論理の四種類の命題の表現がいかになされるのかを見てみよう。まず、全称肯定命題を表現する図1から。ヴェン図の図形は最小部分から構成されているのだが、普通はそのことは表示されていない。しかし、ここでは、さらに分かりやすくするため、単純なケースを考えて、図5のようになっているとしよう(各最小部分に英小文字を付して、それをその最小部分の代理物、すなわち、最小部分が名指している個物の別名とする)。
図5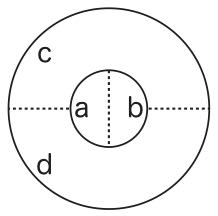
すなわち、円Aは「a」、「b」が付された二つの最小部分から構成されており、円Bは「a」、「b」、「c」、「d」が付された四つの部分から構成されているとしよう。ここで、円Aは性質Aを持つ個物をすべて集めたものの絵であり、円Bは性質Bを持つ個物をすべて集めたものの絵である。すなわち、a、bは性質Aを有しており、それ以外の個物は性質Aを有していない。このa、bを集めたものの絵が円Aである。また、a、b、c、dは性質Bを有しており、それ以外の個物は性質Bを有していない。このa、b、c、dを集めたものの絵が円Bである。この図5(すなわち、図1)を見ると、そこでは、性質Aをもつもの(すなわち、aとb)はすべて性質Bを持つということが描かれていることが容易に見て取れるであろう。つまり、図1では、そのことが主張されているのである。次に、全称否定命題を表現する図2を見てみよう。これは、同じように最小構成部分を明示すると、図6のようになっているとする。
図6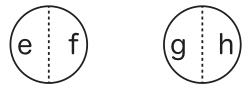
この図を見ると、性質Aをもつもの(すなわち、eとf)はすべて性質Bを持たないと主張されていることが、やはり容易に見て取れるであろう(性質Bを持つのはgとhだけであるから)。次に、特称肯定命題と否定命題を表現する図3と図4を見てみよう。この二つは図形としては同じである。その最小部分は図7のようになっているとしよう。
図7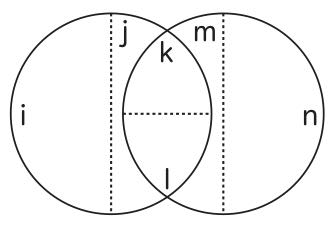
そうすると、性質AとBの両方を持つもの(すなわち、kとl)が存在すると主張されていることが分かるであろう。また、同時に、性質Aを有するが、性質Bを有しないもの(すなわち、iとj)が存在すると主張されていることも分かるであろう(22)。
オイラーのヴェン図の意味を以上のように考えると、おそらく子供でも図1〜4を与えられることで、名辞論理の四種類の定言命題の意味を容易に理解することができるようになると思われる。ただし、オイラー自身がこのようにヴェン図の意味を考えていたとは、彼の叙述からは断言できない。オイラーの「その中に[ある概念が適用される]これらすべての個物を収容している空間[=図形]」(23)という表現から、彼も我々と同じように考えていたのではないかと推測できなくはない。しかし、確定的なことは言えない。我々がこの節で指摘したいのは、オイラーの描いたヴェン図は、我々のように理解すれば教育という目的にかなうものになるだろうということである。オイラー自身の目的も教育にあったのだから、彼も我々のこの指摘を歓迎してくれるのではないかと思う(24)。
四 オイラーのヴェン図の欠点
オイラーのヴェン図が第三節のように理解されても、なおそこには欠点があることを指摘しておかなければならない。我々は第一論文の補遺にあたる論文(25)で、ある仕方で解釈されたヴェン図は何も語らない、と主張した。その仕方とは、ヴェン図の図形は個物を名指す部分から構成されており、図形自体はその部分が名指す個物を要素とする集合を名指す、というものである。先程の図5で考えてみよう。この図は、一見すると、次の文と同じことを主張しているように思える。
集合{a、b}は集合{a、b、c、d}の真部分集合である。
これは数学的真理であり、偽にはなりえない。ゆえに、本来は語るようなことではないのである。しかし、これが語るに値するのは、我々の言語には次のような文も存在するからである。
集合{a、b}は集合{a、b、c、d}の真部分集合ではない。
これは恒偽である。我々の言語は真理も虚偽も語れるようになっており、これが我々の言語が何かを語るということの意味である。他方、今のように理解されたヴェン図は、虚偽を語ることは一切できない。真理は語ることができるのではないかと言われるかもしれないが、その場合、もはや「語る」の意味が変質してしまっている。「語る」という言葉に惑わされないように言うならば、ヴェン図は我々の通常の言語とは本質的に異なるのである。
しかし、我々はオイラーのヴェン図をまさに今述べたように理解したのであり、しかも、それは我々の言語の四種類の定言命題と同じようなものだと見なせると論じたのではなかったのか。この指摘は、後半はそのとおりだが、実は前半が間違っている。何も語らないとされたヴェン図とオイラーのヴェン図には一つ重要な違いがある。それは文字の使用方法である。
まず、何も語らないとされたヴェン図において、文字がどのように使用され得るのかを確認しておこう。もう一度、図5を見てもらいたい。この図の小さな円は、我々の解釈によると、集合{a、b}を指示しているのであり、大きな円は集合{a、b、c、d}を指示しているのであった。今、集合{a、b}に「A」という名前を与え、集合{a、b、c、d}に「B」という名前を与えるとしよう。これはどうしても必要があるからそうしているのではなく、「集合{a、b}」や「集合{a、b、c、d}」という表現が長すぎるので、使いやすい、「A」、「B」という短い別名を用意しているだけである。そしてこの別名を図5に書き込んだものが図1である。なぜ書き込んでいるのかと言うと、これもどうしても必要なわけではないが、そうすることで、「内側の小さな円は集合{a、b}を指示している」の代わりに、「Aは集合{a、b}を指示している」と簡単に言えるようになるからである。なお、このことは先程規約したことだが、図1のような仕方で書き込むことで、「A」は小円の代わりで、「B」は大円の代わりであることが、視覚的に見て取ることもできるであろう。文字の導入が以上のように解された図1は、相変わらず、何も語っていない。なぜなら、A、すなわち、集合{a、b}がB、すなわち、集合{a、b、c、d}の真部分集合であることは、依然として、数学的真理だからである。しかし、図2を見ると、これは集合Aが集合Bの真部分集合ではないことを語っているのではないか、したがって、図2は偽になっているのではないか、と言われるかもしれない。もしもこの主張が正しければ、このタイプのヴェン図も真なる図形と偽なる図形の両方を有しているのだから、我々の言語と同種のものと認められそうである。しかし、この主張は正しくない。図2の最小部分を明示すると、図6になるのであった。したがって、図2は、集合{e、f}は集合{g、h}の真部分集合ではない、ということを語っているのである(便宜上、「語る」という言い方をここで許すことにする)。すなわち、図2は、集合Aが集合Bの真部分集合ではないことを語っているのだが、その際の「A」と「B」は、図1の「A」と「B」とは、別の名前になっているのである。同じ表象システム内の図形であるとすれば、このように同じ名前で別のものを指示することはやめるべきである。したがって、図2は、別名の「C」と「D」を導入して、図8のように描かれるべきなのである。
図8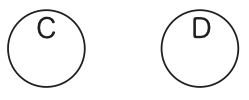
「A」は集合{a、b}の名前であり、Bは集合{a、b、c、d}の名前であると固定すれば、描けるのは図1のタイプの絵(二重円になった絵)だけであり、図2や図3のようなタイプの絵は決して描けないのである(図7に集合名を書き入れると、図3ではなく、名前を変えて、新しく「E」と「F」を導入して、図9のようにしなければならない)。
図9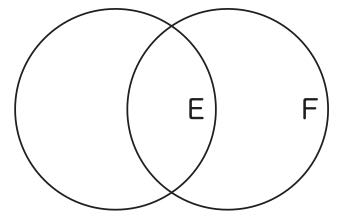
オイラーのヴェン図における文字の使用は、右に述べた方法とは根本的に異なっている。「A」、「B」などの文字は、集合の名前ではなく、性質の名前である。オイラーのヴェン図としての図1は、性質Aを有している個物をすべて集めると、それは、性質Bを有している個物をすべて集めたものの中に完全に収まってしまう、ということを語っている。この場合の集合の関係だけを描くのであれば、先程見たように、文字を使うことは必ずしも必要ではなく、図10を描けば本来は十分である。
図10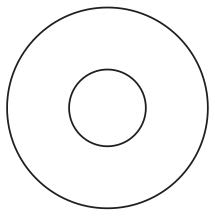
先程は、わかりやすいように文字を書き込んでいただけである。しかし、オイラーのヴェン図の場合、性質と個物および個物の集合の間の関係が問題になっているのであって、したがって、性質を表す文字「A」、「B」は絶対に必要であり、なしで済ますことはできない。必ず、図1のように描かなければならないのである。そして、一般に、性質と個物および個物の集合の間の関係は数学的真理ではなく、偶然的事実であるから、図1は世界のあり方に応じて、真になったり偽になったりする。性質Aを持つものがaとbだけであり、性質Bを持つものがa、b、c、dだけであるとすれば、図1は真である。しかし、もしも性質Aを持つものがeとfだけであり、性質Bを持つものがgとhだけであるとすれば、図1は偽であり、図2が真になる(図2は世界が先程のあり方をしていれば偽だったのである)。図2における「A」と「B」は、異なる図形に付されているが、図1における「A」と「B」と同じ意味を持った記号である。しかしそれは問題を引き起こさない。「A」と「B」は、図形の指示する集合を意味しているのではなく、それとは独立に性質を意味しているからである。このように、オイラーのヴェン図では文字が本質的な構成要素になることで、日常言語の文と同じように、真偽であり得るような何かを語ることができるようになっているのである。
しかし、このことがオイラーのヴェン図の一つの欠点であるというのが、我々がここで指摘したいことである。図11を見てもらいたい。
図11
これは、ある性質、例えば、人間であるという性質を有している個物をすべて集めたものの絵である。そうは見えないと言われるだろうが、図11は最小部分から構成されていると考えられていたことを思い出してほしい。個々の最小部分は一人一人の人間の絵になっているのである。最小部分は人間の形をしていると考えてもよいが、デフォルメされて小さな点で描かれていると考えた方が無理はないだろう。肝心なのは、そうした点が集まって一つのまとまりがある図形を形成することで、人間が集まっている状態を図11は描いている、という点である。このように、図11が人間の集合の絵になっていることは、認めることは難しくないと思われる。しかし、これに文字を加えた図12は、直観的に理解可能な絵になっているとは言い難いのである。
図12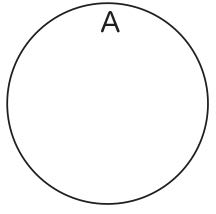
「A」という文字が使われているから、というのがその理由ではない。図13のように、文字ではない何らかの絵を使ったとしても、理解の困難さは変わらない。
図13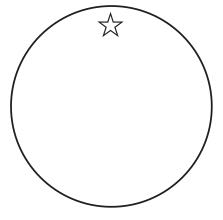
個々の人間のような個物は、一個の点で表象することができるが、人間性のような性質は、普遍であり、個物である点や文字や星印などのインクのシミで表象されるとは考えにくい。表象されるとしたら、それは人為的な規約に大幅に依存することになり、絵画による表象という直観的自明性はかなり失われることになるだろう。また、仮に文字や絵で性質を表すことができたと仮定しても、まだ問題は残る。図12が語ろうとしていることは、円で表されているすべての個物が性質Aを持つということである。この個物と性質の関係が、図12のような絵で視覚的に表現されているとは、およそ思えないであろう。したがって、図12の意味を説明するときには、「性質Aを持つものがここには集められています」というような、本質的に言語の使用に依存した説明がどうしても必要になってくる。すなわち、「・・・は・・・である」という、個物に性質を帰属させる言語的説明が不可欠なのである。したがって、図1〜図4は、名辞論理の四種類の定言命題が言わんとすることを、図形によって十分に説明しているとは言えないのである。これが、オイラーのヴェン図の欠点である。
五 オイラーのヴェン図と空集合の問題
最後に、オイラーのヴェン図の欠点であると一般に考えられている別の問題を取り上げて、それを、前節で指摘した文字の本質的使用という観点から検討してみたい。その一般に考えられている欠点とは、オイラーのヴェン図は空集合を表すことができないのではないか、という問題である(26)。オイラーのヴェン図では、性質Aを持つものの集合は図12で表されるのであった。しかし、この円は最小部分から構成されており、それは何らかの個物を名指しているのであった。そして、この円はこの個物を要素として含む集合を表しており、当然、それは空集合ではない。このように考えれば、この指摘は正しいように思われる。あるいは、以下のように論じることもできそうである。すなわち、「全称肯定命題「すべてのAはBである」と全称否定命題「すべてのAはBでない」の両方が真であれば、Aであるものの集合が空であることが論理的に帰結する。したがって、全称肯定命題を表している図1と全称否定命題を表している図2を同時に描けば、空集合を描くことができるはずである。しかし、これらを同時に描くことはできない(円Aを円Bの内部に置き、かつ、外部に置く、ということは不可能である)。よって、オイラーのヴェン図では空集合を描くことはできないのである」と論じることもできそうである(27)。しかし、以上のような議論にも関わらず、オイラーのヴェン図で空集合を表すことが可能であることを以下で示したい。
オイラーのヴェン図の基本は、存在しないものは描かない、ということにある。このことは、四種類の定言命題を表している図1〜図4だけを見たのではあまりはっきりしないかもしれないので、図1を例に、どうなっているのかを詳しく見てみよう。図14を見てもらいたい。
図14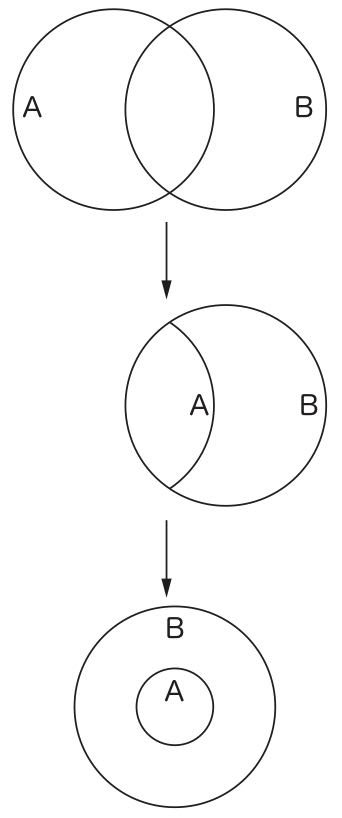
まず、我々は出発点で非常に寛大な存在論を取っているとしよう。つまり、あらゆる種類のものが存在すると考えているのである。具体的には、AではあるがBではないもの、AでありかつBでもあるもの、AではないがBであるもの、これらの三種類のものがすべて存在していると考えるのである。この考えを図で表現したものが、図14の一番上の図である。次に、我々は、探求の結果、AではあるがBではないものが一つも存在しないことを発見したとする。この発見を描いたのが、図14の真ん中の図である。これは、これまで描いていた、AではあるがBではないものを消去したのである。これを体裁を整えるために描き直したのが図14の一番下の図であり、これがすなわち全称肯定命題を表現している図1である。このように、図1は、AではあるがBではないものを描かないことによって、そうしたものの集合が空であることを表現しているのである。
オイラーはAであるものの集合が空である場合を考慮する必要がなかったので、そうした図を描いていないが、我々がこれを敢えて描くとすれば、図15になるであろう。
図15
すなわち、Aであるものは存在しないのだから、何も描かないのである。実際、オイラーのヴェン図の改良に取り組んだパースも、本来のオイラーの図形をそのようなものと理解していて、オイラーの図形では、Aであるものが存在しない場合は、図16になると述べている(28)。
図16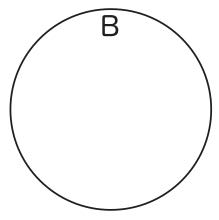
図16は、Aであるものが存在しないこととBであるものが存在していることの両方の事態の図を同時に描いている。そこで、後者の事態を描くことをやめて、その図を消せば、まさに、図15とおなじになるのである(29)。しかし、図15には、何も描いていないので、何を描いていないのかも分からない、という問題がある。いかなる種類のものも一切存在しないという状況を描くのであれば、図15でも良いだろうが、ここでは、特定の種類のものが存在しないということを主張したいのである。しかし、幸いなことに、前節で指摘したように、オイラーのヴェン図には文字が本質的な構成要素として含まれている。したがって、Aであるものの集合が空であることのオイラーのヴェン図による表現は、図17として、問題なく行うことができるようになっているのである。
図17
全称肯定命題と全称否定命題を同時に描くことができないという問題は、次のようにして解消される。Aであるものが存在しない場合の全称肯定命題は図18によって表現され、全称否定命題は図19によって表現される。
図18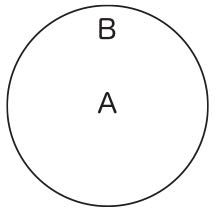 図19
図19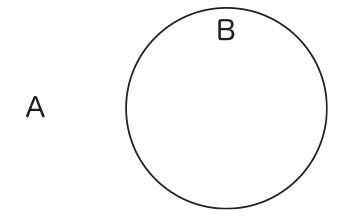
これを同時に重ねて描くことに何ら問題はなく、それは図20になる。
図20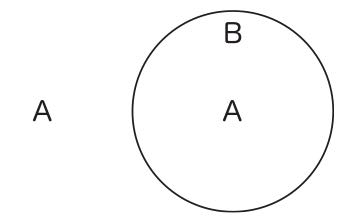
もちろん、図20によって初めてAであるものの集合が空であることが描かれた訳ではなく、最初から、図18と図19でも描かれていることである。Aであるものは存在しないのだから、そうしたものが最初から描かれないのは当然のことなのである。
以上のように、オイラーのヴェン図では、文字を使用することによって、空集合の表現ができるようになっているのである。これは文字使用の利点であるかもしれないが、前節で指摘したように、文字の使用はオイラーのヴェン図の図形としての性格を著しく損なうものであることは、強調しておかなければならない。この文字使用という難点を克服したと考えられるのが、ヴェンによるヴェン図なのであるが、これについては稿を改めて論じることにしたい(30)。
註
(1)現在(本稿執筆時点の二〇二〇年)の高等学校の数学では論理学を教えることはほとんどなくなったが、一つだけ例外的に教えられているものがある。名辞論理学で導入される四つの定言命題のうちの一つである全称肯定命題(伝統的に「A命題」と略され、現代論理学では「形式含意」と呼ばれるもの)がそれである。高校の数学Iや数学Aの教科書でも全称肯定命題を解説するためにヴェン図が使われている。なお、四つの定言命題については、本論文の第二節で説明する。
(2)連続研究の第一論文は、橋本(二〇一六)である。その補遺にあたる論文が橋本(二〇一七)である。本論文は独立して理解可能となるように、これら先行する論文の内容を一部繰り返したところがあることをことわっておく。
(3)橋本(二〇一六)参照。本論文第三節でも再説する。
(4)Venn 1880, Venn 1881.
(5)Peirce 1933, Book II: Existential Graphs, Chapter 1: Euler's Diagrams.
(6)本論文では「命題」を「文」と同義なものとして使用する。すなわち、「命題」によって意味を持った記号列である文を表すものとする。註(1)の「A命題」のように、伝統的用語として「命題」という語を使わなければならないときがあるので、「文」という語には統一しなかった。
(7)定言命題から派生して仮言命題や選言命題が得られるが、ここでは名辞論理学の定言命題しか扱わないので、以下、「定言」を省略して、単に「命題」と書いただけでも、定言命題のことを意味させることにする。
(8)実際は主語と述語を交換することで、「すべてのBはAである」、「すべてのBはAでない」、「あるBはAである」、「あるBはAでない」が得られ、全部で八個の命題が存在することになる。しかし、伝統的には、主語と述語の中身と位置をABと固定した上で、それに対して肯定/否定と全称/特称の操作を施すと何個の命題が存在するかを考え、それは本文のAEIOの四命題だけだと考えている。このことは普通は問題にならないが、名辞論理を一般的に考察するときに、若干、問題になるので、注意しておいてもらいたい(後続する別論文で扱う予定である)。
(9)新版の日本語訳アリストテレス全集で『分析論前書』の翻訳を担当した今井知正は、アリストテレス自身の体系がメレオロジーの体系として解釈される可能性を指摘し、それを踏まえてアリストテレス論理学の「意味論と証明論がどのようなものとなるかという問題を改めて検討することが今後の研究課題となるであろう」と述べている(今井(二〇一四)、五四三頁)。
(10)最初にはっきりと記号化して示したのは、おそらくフレーゲの『概念記法』であると思われる。Frege 1879, pp. 23-4[日本語訳、四〇―一頁]参照。
(11)「オイラーのヴェン図」という言い方は奇妙に思われるかもしれないが、本論文では、集合を表すために使われる図形をすべて無差別に「ヴェン図」と呼ぶことにするので、このような一見すると奇妙な言い方も出てくることになる。なぜすべてを「ヴェン図」と呼ぶのか、その理由については、橋本(二〇一六)、一―二頁を参照されたい。
(12)現在、この流れを担っている代表者はシン・ソンジュであり、彼女の『図形の論理的地位』(Shin 1994)の出版以降、ヴェン図をはじめとした図形表現の研究はふたたび活発になっている。
(13)マーガレット・E・バロンは、十三世紀のカタロニアの神秘主義者、宣教師であるラモン・リュイ(Ramon Llull, c. 1232-1315)がヴェン図を用いていたことを報告している(Baron 1969, p. 115)。また、彼女は、ゴットフリート・ヴィルヘルム・ライプニッツがオイラーと同じようなヴェン図で四種類の定言命題を表現していたことも紹介している(Baron 1969, pp. 116-7)。ライプニッツのヴェン図は Leibniz 1686 で見ることができる。オイラーがライプニッツのヴェン図を見ていたかどうか、実際のところは分からない。しかし、彼女が指摘している、特称命題を図形で表す際のライプニッツの方法は、オイラーの方法(本文で後に見ることになる)とまったく同じである。全称命題の表示方法が同じになることは十分考えられることだが(そのことが本論文の主題の背景でもある)、特称命題の表示方法がまったく同じになることは、偶然とは考えにくい。したがって、オイラーがライプニッツのヴェン図を見ていた可能性はかなりあると思われる。
(14)Euler 1768-73, vol. 1, p. 1.[English translation, vol. 1, p. 1.]一七六〇年四月一九日の日付がある第一回目の手紙の冒頭部分に、このことを窺わせる記述がある。なお、オイラーの手紙に言及したり、そこから引用する場合は、フランス語で書かれている原典を使用したが、[ ]内に挙げてある英訳も参考にした。以下においても同様である。
(15)Euler 1768-73.
(16)Euler 1768-73, vol. 2, p. 98.[English translation, vol. 1, p. 396.]一〇二回目の手紙から一〇八回目の手紙までが論理学の解説にあてられており、そのうち最初の四回の手紙でヴェン図が用いられている。(英訳版では、図形そのものは番号をつけられて別紙にまとめて置かれていて、本文ではその番号への参照が書かれているだけである。したがって、英訳版の三九六頁を開いても、そこに図形自体を見ることはできない。)
(17)フリーデリーケ・シャルロッテの妹のルイーゼ・ヘンリエッテ・ヴィルヘルミーネ(一七五〇―一八一一)も同時に授業を受けていた可能性がある。そうすると、このとき、妹の方は十歳である。
(18)Euler 1768-73, vol. 2, pp. 100-1.[English translation, vol. 1, p. 397.]
(19)Euler 1768-73, vol. 2, p. 98.[English translation, vol. 1, p. 396.]オイラーは、名辞が意味するのは性質ではなく概念(notion)であると考えている。もちろん、性質と概念は同一視できない。しかし、今、問題になっているのは、普遍と個物の関係であり、普遍は性質として外界に実在するのか、概念として心の中にしか存在しないのか、という普遍論争にここで関わる必要はない。そこで、論述を簡潔にするために、オイラーの「概念」を「性質」と読み替えることにする。また、オイラーは、「図形(figure)」の代わりに「空間(espace)」という言葉も用いていて、具体的にどういう形をしているかは重要ではないから、「図形」より「空間」の語の方がふさわしいと述べているが(Euler 1768-73, vol. 2, p. 100[English translation, vol. 1, p. 397])、ここでは「ヴェン図」という用語を用いているので、「図形」という用語に統一した。
(20)Euler 1768-73, vol. 2, pp. 99-100.[English translation, vol. 1, pp. 396-7.]
(21)橋本(二〇一六)、一八頁以降。
(22)特称肯定命題と同じことだけを描いているヴェン図や、特称否定命題と同じことだけを描いているヴェン図はないのかと疑問に思われるかもしれない。オイラーは、図形は同じままだが、文字の置き方を変えることで、この二つの区別を行っている。すなわち、特称肯定命題を描く図3では、文字「A」が中央のレンズ状の図形の中に置かれており、特称否定命題を描く図4では、文字「A」が左側の三日月型の図形の中に置かれている。しかし、この文字の位置の違いが何を意味しているのかは、あまりはっきりとはしていない。この問題は、ヴェンとパースによるヴェン図を論じる後続の別論文で論じる予定である。なお、文字の位置による特称肯定命題と特称否定命題の区別の方法が、註(13)で触れた、ライプニッツが特称命題を図形で表示する際に使った方法なのである。
(23)Euler 1768-73, vol. 2, p. 98.[English translation, vol. 1, p. 396.]
(24)エリック・ハンマーとシンは、オイラーの図形の意味は次の二つの規約に基づいていると主張している。
「規約I:ある集合、例えば集合Aは、文字「A」が付された円によって囲まれた領域によって指示される。
規約II:個体領域内の各々の対象xは、それに固有の平面上の位置によって指示される。その位置をIxとする。ただし、Ixは以下の条件を満たすものとする。すなわち、Ixが「A」とレッテルを貼られた円の中にあるのは、xが集合Aの成員であるとき、かつ、そのときに限る、という条件である。」(Hammer and Shin 1998, p. 4.)
これは我々の提案したヴェン図理解を正確な言葉で表現したものと見なすこともできる。しかし、この規約に基づいてヴェン図を理解せよ、と子供に求めるのは無理であろう。我々のように、ヴェン図の図形は物が集まっている様子を描いているのだと、簡単に分かりやすく述べたほうが、教育という目的にはかなっていると思われる。
(25)橋本(二〇一七)。
(26)例えば、ハンマーは「いかなるオイラー図もA[であるものの集合]が空であることを主張することはできない」(Hammer 1995, p. 75)と述べている。
(27)これは基本的にシンの指摘(Shin 1994, p. 16)と同じことである。
(28)Peirce 1933, paragraph 356. ただし、パースはそこで文字として「S」、「P」を使っているが、ここでは本論文での文字使用に合わせて、それぞれ「A」、「B」に変更した。また、パースは文字を円の外側に置いているが(印刷されたページでは、円の輪郭に文字が少し重なっているように見える)、ここではオイラーの本来の書き方に従わせるため、円の内側に文字を置いた。円はどういう性質を持つものを集めてできているのか、そのことを表すことを目的に文字を使用するのであれば、文字を円の内側に置くか外側に置くかは問題にならないだろう。内側に置く方が円と文字の結びつきが直観的によりはっきりすると感じるものもいるであろうが、文字を外側に置いても、十分近接している限り、文字と円の結びつきは明瞭であろう。実際、多くの場合、図のレッテルは図の外部に付されるのが普通である(図の内部に書き込んだりすると図を汚すことになるので)。しかし、オイラーは、註(22)で指摘したように、別の目的のためにも文字を使用しているので、文字は円の内側と外側のどちらでも良い、ということにはならない。註(22)で見た、特称肯定命題の図(本文中の図3)と特称否定命題の図(本文中の図4)の違いを、文字を円の外側に置いて描き直すと、それぞれ図21と図22になるだろう。
図21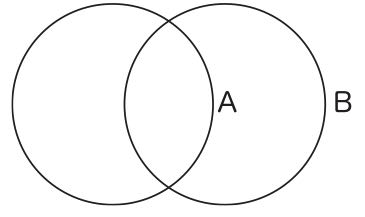 図22
図22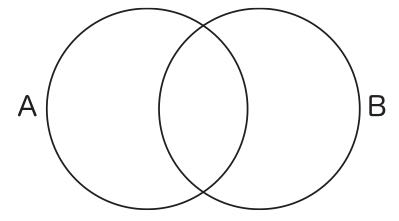
しかし、図21が中央のレンズ状の図形の存在に注意を促し、図22が左側の三日月型の図形の存在に注意を促しているようには、あまり見えないだろう。そういうものだと規約することは簡単だが、直観的自明性は失われ、この図形のヒューリスティックな性格はなくなるであろう。したがって、子供に教えているオイラーにとっては、円の内側に文字を置くということは重要なことであったと思われる。他方、パースは文字をこの第二の目的では使用していないので、文字の位置が内側であれ外側であれ、どちらでも良いのである。そのため、本文の図16では、文字を円の内側に置くという変更を加えたが、そのことはパースにとって問題にはならないのである。では、パースは特称肯定命題と特称否定命題の区別をどのようにつけたのかという疑問が、当然、生じるであろう。彼は、まったく別の記号「×」を導入して、この区別をつけたのである。すなわち、彼は、特称肯定命題を図23、特称否定命題を図24のように描いたのである(Peirce 1933, paragraph 359)。
図23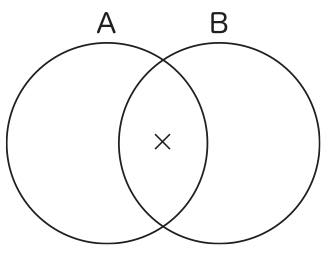 図24
図24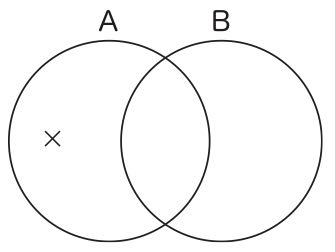
ここで文字「A」と文字「B」はパースのオリジナルにしたがって円の外部に置いているが(先に注意したように、実際は「S」、「P」という文字が使われている)、これを内部に置いたとしても、「×」の位置が変わらない限り、何の問題も生じないことは明白である。しかし、「×」は注意を促したい部分(図23では中央のレンズ状の図形、図24では左側の三日月型の図形)の内部に置かれていることに注意してもらいたい。「×」は外部ではなく、内部に置かれるべきであるように思われるのである。この問題に関しては、現在準備中の別論文で論じる予定である。
(29)パースは註(28)で言及したパラグラフで、オイラーの本来の図形ではAであるものもBであるものも存在しない場合を描く方法があると述べている。当然、それは図15と同じになると思われるのだが、印刷されたページを見る限りでは、図15のような完全な空白がその方法であったのかは、必ずしも明瞭ではない。
(30)匿名査読者からの指摘によって、いくつかの箇所で論述を改善することができました。感謝いたします。
文献
- Baron, M. E. 1969. “A Note on the Historical Development of Logic Diagrams: Leibniz, Euler and Venn”, The Mathematical Gazette 53: 113-25.
- Euler, L. 1768-73. Lettres à une princesse d’Allemagne sur divers sujets de physique & de philosophie, 3 vols. Imprimerie de l’Académie Impériale des Sciences. [Letters of Euler on Different Subjects in Physics and Philosophy Addressed to a German Princess, translated by Henry Hunter, 2 vols. second edition, Murray and Highley; J. Cuthell; Vernor and Hood; Longman and Rees; Wynn and Scholey; G. Cawthorn; J. Harding; and J. Mawman, 1802.]
- Frege, G. 1879. Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. Luis Nebert.[G・フレーゲ、『フレーゲ著作集1 概念記法』、藤村龍雄(編)、勁草書房、一九九九年。]
- Hammer, E. M. 1995. Logic and Visual Information. CSLI Publications.
- Hammer, E. and Shin, S. 1998. “Euler’s Visual Logic”, History and Philosophy of Logic 19: 1-29.
- Leibniz, G. W. 1686. “De Formae Logicae Comprobatione per Linearum ductus”. 「論理形式の作図による証明」、『ライプニッツ著作集1』、下村寅太郎、山本信、中村幸四郎、原亨吉(監修)、澤口昭聿(訳)、工作舎、一九八八年、二一五―六二頁。参照は後者。
- Peirce, C. S. 1933. Collected Papers of Charles Sanders Peirce, Vol. IV: The Simplest Mathematics. Harvard University Press.
- Shin, S. 1994. The Logical Status of Diagrams. Cambridge University Press.
- Venn, J. 1880. “On the Diagrammatic and Mechanical Representation of Propositions and Reasonings”, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, S. 5, Vol. 9, No. 59: 1-18.
- ------ 1881. Symbolic Logic. MacMillan. 2nd edition, 1884. References to the latter.
- 今井知正、二〇一四、「『分析論前書』解説」、『アリストテレス全集2』、岩波書店、五二九―七四頁。
- 橋本康二、二〇一六、「集合演算とヴェン図」、『哲学・思想論集』四一号、一-二六頁。
- ―――― 二〇一七、「ヴェン図は何かを語るのか? ――『論理哲学論考』的観点からの言語哲学的考察――」、『哲学・思想論集』四二号、一―三三頁。
Term Logic and Euler Diagrams
Kouji Hashimoto
Euler diagrams are used for representing categorical propositions. For example, a universal categorical proposition “All A are B” is represented by the following diagram:
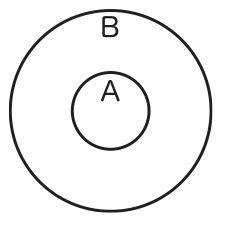
In this paper, I explore why Euler diagrams facilitate our understanding of categorical propositions. Just as a set is composed of its members, a circle in Euler diagram is composed of several parts, for example, as follows:
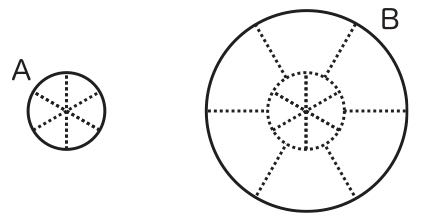
What is A is referred to by a part of the smaller circle, and what is B is referred to by a part of the larger circle. By this composition, the fact that the circle tagged with the letter “A” is in the circle tagged with the letter “B” in the above figure tells us, in an intuitively self-evident way, that all A are B. It is pointed out, however, that the use of letters such as “A” and “B” in Euler diagrams is not intuitively obvious. Euler diagrams are not fully visualized representations of categorical propositions.
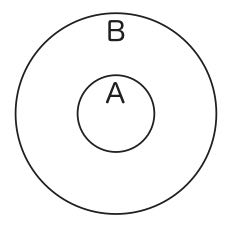 図2
図2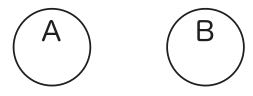
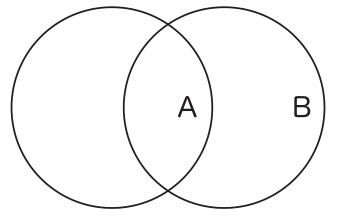 図4
図4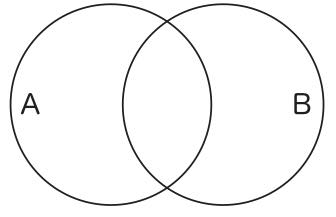
 図2
図2
 図4
図4













 図19
図19

 図22
図22
 図24
図24

