集合演算とヴェン図
橋本康二
ヴェン図は、その形がきわめて印象的であり、また、教育現場でよく用いられるせいもあって、ほとんどすべての人にとってなじみがある図形であると思われる。しかし、おそらく見る者だけでなく描く者にとっても、ヴェン図が正確には何を行っているのかは、あまり明瞭には理解されていないのではないだろうか。ヴェン図の理解を困難にしている理由の一つは、それがいくつかの異なる分野で異なる目的のために使われていることにあるのではないかと思われる。そこで、本研究では、ヴェン図が用いられている代表的な分野を区別し、それぞれの分野においてヴェン図がどのような意味を持っているのかを探求することを試みる。その際、歴史的事情も踏まえ、それぞれの分野で実際にどのような意味で使われているのかを考慮しつつ、最終的には、それぞれの分野での目的を達成するためにヴェン図はどのような意味を持つべきであるのかを明らかにしたい。
ヴェン図をめぐる哲学的考察を行う本研究は三つの論文から構成される。第一論文(本論文)では、集合演算で使用されるヴェン図を取り上げ、集合演算の結果を表示するためのヴェン図はどのように理解するべきなのかを考察する。続く第二論文では、名辞論理で使用されるヴェン図を取り上げ、名辞が表す概念間の関係を表示するためのヴェン図はどうあらねばならないのかを考える。最後の第三論文では、命題論理で使用されるヴェン図を取り上げ、ヴェン図は真理関数としての命題を表示することができるのかを検討する。
「ヴェン図」という言葉の使用方法についてあらかじめ注意しておきたい。本研究では初等的集合論や論理学の文脈に見いだされる、一つ以上の四角形や円などを組み合わせた図形を「ヴェン図」と呼ぶことにする。つまり、一般に「ヴェン図」と呼ばれているものを本研究でもそのまま「ヴェン図」と呼ぶのである。したがって、例えば、「オイラー図(ないしオイラー円)」と呼んで区別することがある特徴的な図形も本研究では「ヴェン図」と呼ぶことになる。厳密な定義を与えて、ヴェン図の創始者とされるジョン・ヴェン(一八三四-一九二三)が意図していた図形だけを「ヴェン図」と呼ぶこともできるだろうが、そうすると、現在「ヴェン図」という名前で流通しているほとんどすべての図形が「ヴェン図」とは呼べなくなるので、このようにルーズな仕方で「ヴェン図」という言葉を使うことにするのである(1)。
二十世紀の後半、いわゆるスプートニク・ショック以後、日本では「数学教育の現代化」という名のもとで数学教育の見直しが行われ、集合が算数・数学の基礎をなす概念として導入されることになった。そのため、小学校の段階でヴェン図に接することが普通となった。ただし、現在(本稿執筆時点の二〇一五年)では、集合を基礎にして数学を教えるという方法は影を潜め、集合は一つの単元として高等学校の数学Iないし数学Aで初めて教えられ、多くの学生はそこで初めてヴェン図を見ることになるようである(2)。この高校数学の集合の扱いに関して、数学教育に深い関心を持つ論理学者の本橋信義は次のような指摘を行っている。
「中学や高校で集合の話をするときに、ベン図という図を使って説明することがあります、しかし、本来、J・Vennが意図した意味でベン図が用いられていることはほとんどないようです。本来のベン図は、〝集合と集合の間の関係〟を表示するための方法でした。しかし、教科書などで用いられているベン図は、〝集合演算の結果〟を表示するための方法として用いられています。」(3)
この論文では、ヴェン図が集合演算の結果を表示するとはどういうことなのかを検討する。集合と集合の間の関係を表示するヴェン図は続く第二論文において検討する。
集合演算とは一つ以上の集合を引数にとり、一つの集合を値にとる関数のことである。代表的な集合演算として、一変数集合演算のXc、二変数集合演算のX∩YとX∪Yがある。Xcは、集合Aを引数にとった場合、Aの要素ではないもののすべてからなる集合を値にとる。この値はAの「補集合」と呼ばれる。X∩Yは、集合AとBをそれぞれの引数にとった場合、AとBの両方の要素になっているもののすべてからなる集合を値にとる。この値はAとBの「共通集合」と呼ばれる。X∪Yは、集合AとBをそれぞれの引数にとった場合、AとBのどちらかの要素になっているもののすべてからなる集合を値にとる。この値はAとBの「合併集合」と呼ばれる(4)。こうした補集合、共通集合、合併集合を表示するために、高等学校の数学の教科書では、図1のようなヴェン図が使われている。
そこでまず問題にしなければならないことは、そもそも図形が集合を表示するとはどういうことなのか、ということである。以下では図形で集合を表示するための一つの方法を提示し、それが集合演算の結果を表示するという目的にかなっているかを吟味してみよう。
集合はものの集まりだが、最初にものの集まりを一つ決め、その中でものの集まりを考えることが普通である。この最初にとられるものの集まりは「全体集合」と呼ばれ、「U」と略記される。ここでは全体集合として自然数全体の集まりをとることにする。この全体集合を表示するための記号として、図2の長方形を用いることにしよう。
図2
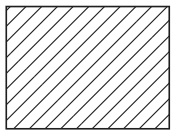
長方形というのは四本の線分のことではなく、それで囲まれた内部の領域、すなわち、四本の線の内部の点全体の集まりのことである。したがって、むしろ図3のように斜線を入れて描いた方が良いかもしれない。
図3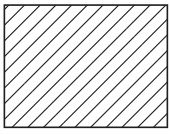
以下、長方形が何回もページの上に描かれるが、特に断りがない限り、すべて自然数全体の集合を表示するものとする。次に、自然数の適当な集合を考える。例えば、2の倍数の集合を考えて、これに「A」という名前を付ける。この集合を表示するために、長方形の内部の円である図4を用いることにする。
図4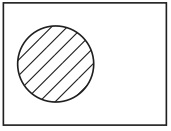
今後、特に断りがない限り、この長方形内部のこの位置にある円はすべて2の倍数の集合を表示するものとする。次に、3の倍数の集合を考え、これに「B」という名前を付け、これを表示するために、図5の円を用いることにする。
図5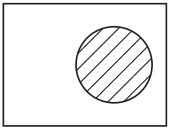
同様の方法で好きなだけ集合を考えて、それを表示するための図形を定めて行くことができる。しかし、その前に立ち止まって考えておいた方が良いことがある。それは、全体集合Uの中に集合Aを導入したとき、実は既にもう一つ別の集合が導入されていたということである。その集合とは、Aの要素ではないものの集合、すなわち、2の倍数ではない数の集合、つまり、Aの補集合Acである。全体集合の中に一つの集合を導入するとは、それを二つの集合に二分割することに他ならないのである。したがって、この補集合Acを表示する方法を有しておいた方が良いだろう。そのために図6を用いることにする。
図6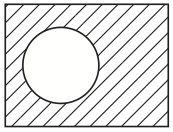
さらにさかのぼって考えると、全体集合Uを導入したときに既にもう一つ別の集合を導入していたことが分かる。それは、Uの内部でUの要素ではないものの集合である。そうしたものは存在しないから、この集合は「空集合」と呼ばれ、「φ」という名前が付けられる。これを表示するためには図7を用いることにする(図7は長方形の外部に広がっている領域である)。
図7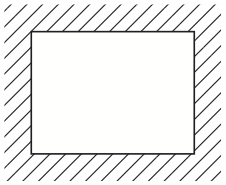
したがって、Uの中に一つの集合Aを導入すると、実際には4個の集合(U、φ、A、Ac)を導入したことになるのである。
では、Uの中に二つの集合AとBを導入した場合、実際にはいくつの集合を導入したことになるのだろうか。すべてのものは、Aの要素であるか否か、Bの要素であるか否か、という二つの二者択一的観点から分類されるので、22=4個の集合に分割される。すなわち、Uは、A∩B、A∩Bc、Ac∩B、Ac∩Bcの4個に分割される。しかし、これですべてではない。この22=4個の集合から任意の集合を取り上げて、その合併集合を作ることができるので、以下の222=16個の集合が得られる(この中にはA、B、U、φと先の4個の集合も含まれていることに注意)。
φ
A∩B
A∩Bc
Ac∩B
Ac∩Bc
(A∩B)∪(A∩Bc) [=A]
(A∩B)∪(Ac∩B) [=B]
(A∩B)∪(Ac∩Bc)
(A∩Bc)∪(Ac∩B)
(A∩Bc)∪(Ac∩Bc) [=Bc]
(Ac∩B)∪(Ac∩Bc) [=Ac]
(A∩B)∪(A∩Bc)∪(Ac∩B) [=A∪B]
(A∩B)∪(A∩Bc)∪(Ac∩Bc) [=A∪Bc]
(A∩B)∪(Ac∩B)∪(Ac∩Bc) [=Ac∪B]
(A∩Bc)∪(Ac∩B)∪(Ac∩Bc) [=Ac∪Bc]
(A∩B)∪(A∩Bc)∪(Ac∩B)∪(Ac∩Bc) [=U]
したがって、これらの集合を表示するためには16個の図形を用意しなければならない。ただし、4個は既にあるので、あと12個必要である。面倒な作業のように思われるかもしれないが、実はそうではない。ここで、基本となるU、A、Bの図形である図3、図4、図5を「基本図形」と呼ぶことにしよう。
この三つの図形を重ね合わせ、斜線を消して輪郭だけを残すと図8になる。
図8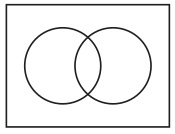
すると、図8の中に互いに重なっていない4個の図形があることが見て取れるであろう(5)。この4個の図形を「最小図形」と呼ぶことにしよう。長方形は図9〜12の4個の最小図形に分割されているのである。
そうすると、この4個の図形から任意の図形を取り上げて、それを組み合わせて一つの新しい図形を作ることができるので、24=16個の図形が得られる。ただし、0個の図形を取り上げて組み合わせても図形はできないので、それは空集合の図形(図7)で代用することにする。
図7
また、取り上げられた図形が互いに接していなくても、まとめて一つの図形になっていると見なすことにする。かくして、導入された集合の個数とちょうど同じ個数の図形が幸運にも得られたのだから、図13のように、これをそのまま集合を表示するための図形として用いることができるのである(6)。
図13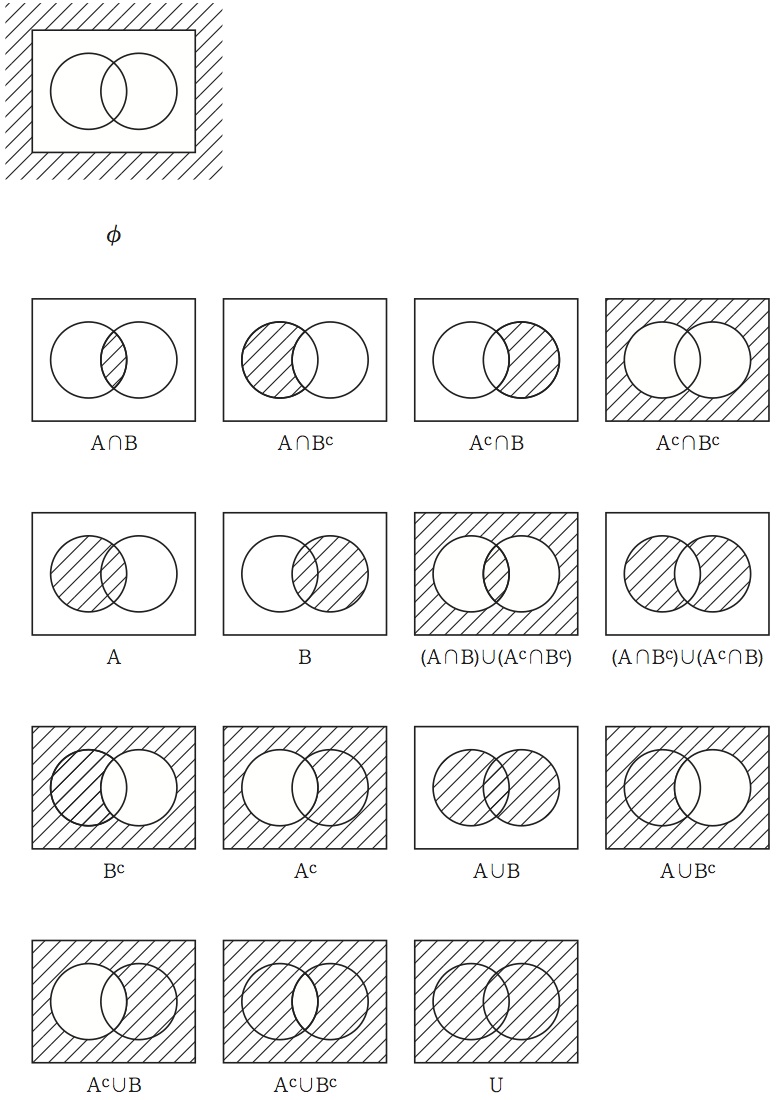
一般に、Uの中にn個の集合を導入した場合(これらを「基本集合」と呼ぶことにする)、Uは2n個の集合に分割され(これらを「最小集合」と呼ぶことにする)、そこから任意の集合を取り上げて合併集合を作ると、全部で22n個の集合が得られる。これらの集合を表示するためには22n個の図形が必要になるが、これだけの個数の図形をどのようにしたら用意できるだろうか。右ではn=2の場合、1+n=3個の基本図形を用意するだけで22n=16個の図形が自動的に得られるということが示されたが、実は、このことを一般化することができる。すなわち、任意のnに関して、1+n個の基本図形をある仕方で用意するだけで22n個の図形が自動的に得られるのである。そのことは以下のように証明される。
まず、長方形の中に何らかの仕方でk個の基本図形を描く(これは、これまでのプロセスでの円を描いたことに相当する)ことで合計1+k個の基本図形を準備したところ、2k個の最小図形が得られた、すなわち、長方形が2k個の図形に分割された、と仮定しよう。この最小図形を任意に組み合わせると22k個の図形が得られる。このとき、長方形の中にk+1個目の基本図形を次のように描き込むことで、合計1+(k+1)個の基本図形を準備する。すなわち、既に存在する最小図形とちょうど一度だけ重なるようにし、その際、決してその最小図形の全体を覆わないように、新しい基本図形を描くのである。そうすると、既存の最小図形の各々が、新しく導入された基本図形に重なっている部分と重なっていない部分の二つに分割されることになり、最小図形の個数は二倍になる。つまり、2k・2=2k+1個の最小図形が得られるのである。その結果、この最小図形を任意に組み合わせることで22k+1個の図形が得られるのである。なお、このような図形の描き方こそヴェンが論文「命題と推論の図形的機械的表示について」(一八八〇)の中で考案したものである(7)。
n=0のとき、長方形の中には何も描かないでおくことで1+n=1個の基本図形(すなわち長方形自体)を用意することになる。このとき、最小図形も長方形となり、その個数は1(=20)個である。したがって、これらが任意に組み合わされた、図14の2(=220)個の図形が存在する。
図14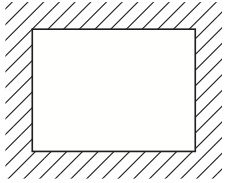
以上が基底となるので、数学的帰納法により、任意のnに関して、1+n個の基本図形を用意するだけで22n個の図形が得られることが証明された。
ヴェンが考案した基本図形の導入の方法を具体例で見ておこう。まず、長方形に1個の基本図形を付け加える場合を考える。このとき、図15はヴェンの方法に反している。
図15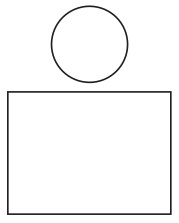
追加された円が既存の最小図形である長方形とまったく重なっていないからである。図16の円は長方形と重なっているが、その全体を覆ってしまっているので、やはりヴェンの方法に反している。
図16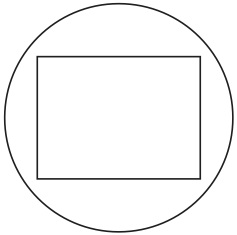
図17はもとの長方形と同じ長方形を新たな基本図形として導入したものである。
図17
このこと自体は禁じられていないが、新しい長方形はもとの長方形の全体を覆っているので、これもヴェンの方法に違反している。図18で導入されている閉曲線は長方形の全体を覆うことなく部分的に重なっているが、二カ所で重なっているので、ヴェンの方法に反している。
図18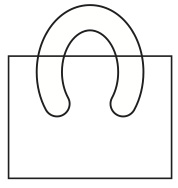
図19はヴェンの方法には反していない。
図19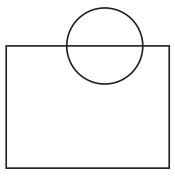
というのも、ヴェンは全体集合を表す長方形を用いていないので、それに関する規則を持っていないからである(8)。しかし、我々は全体集合の長方形の中に基本図形を導入するように定めているので、これは認められないのである。我々固有のこの規則も満たすためには、図20のようにするしかない。
図20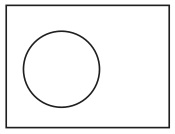
次に、長方形に2個の基本図形を付け加える場合を考える。このとき特に注意しなければならないのは図21と図22である。
図21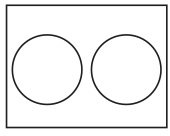 図22
図22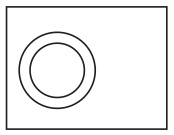
図21は既存の(長方形に1個の基本図形を描いたときに存在する)最小図形の一つ(図24)と重なっているが、もう一つ(図23)とは重なっていない。図22は図23とは重なっているが、図24とは重なっていない。
図23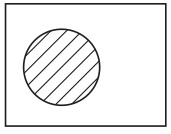 図24
図24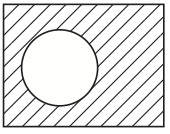
よって、ヴェンの方法に反しているのである。既存のすべての最小図形(図23と図24)の一部と重なるように2個の基本図形を描くと、図25のようにならざるを得ない。
図25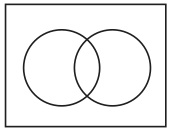
ヴェンの方法に従って長方形の中に3個の基本図形を導入すると、図26になる(23=8個の最小図形と223=256個の図形が得られる)。
図26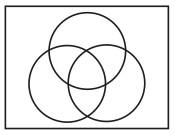
4個の基本図形を導入しようとすると、円ではどうしてもうまくいかないことがわかる。しかし、ヴェンは楕円を用いて図27のように作図する方法を発見した(24=16個の最小図形と224個の図形が得られる)(9)。
図27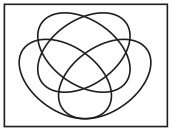
このように、ヴェン図はどんどん複雑になって行く。そうすると、ヴェンの方法に従って長方形の中に基本図形を導入することは、ある程度の個数になると幾何学的な制約により不可能になるのではないだろうか、という懸念が生じる。もしも不可能ならば、先ほどの数学的帰納法による証明は無効になってしまう。だが、幸いなことに、T・モアの「ヴェン図の作図について」において、ヴェンの方法に従って長方形の中に任意の有限個数の基本図形を導入することが幾何学的に可能であることが証明されているので、先の証明の有効性は保証されているのである(10)。
以上で、n個の基本集合を導入したとき、集合演算により22n個の集合が存在することになるが、そのすべてを図形で表示する一つの方法を示した。では、高等学校の数学の教科書に見られる、集合演算の結果を表示するためのヴェン図は、このように規定されたヴェン図として理解されるべきなのであろうか。否、そうは思われないのである。
例として、図13の「A∩B」というキャプションが付された図を見てみよう。
図13, A∩B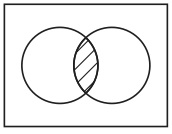
これは集合A(2の倍数の集合)と集合B(3の倍数の集合)の共通集合(6の倍数の集合)を表示している。なぜなら、そうなるように我々が図形の意味を規約したからである。したがって、集合演算の結果を表示するということだけが目的であるならば、我々のこの図を使うことで、その目的は十分に達成されている(11)。だが、高校数学のヴェン図の目的がこれだけとは考えにくいのである。この目的のためなら、「AとBの両方の要素になっているもののすべてからなる集合」、「AとBの共通集合」、「A∩B」、「6の倍数からなる集合」などの表現で十分であり、わざわざ手の込んだ図形を記号として導入する必要などないはずである。高校数学のヴェン図の目的はむしろヒューリスティックなものもあるのではないかと思われる。教師が、集合を学び始めたばかりの生徒に対して共通集合という概念を教えるとき、まず、「共通集合とはAとBの両方の要素になっているもののすべてからなる集合のことだ」と言う。次に、ヴェン図を示して、「つまり、この図が示している集合のことなんだ」と補足する。言葉による最初の説明で理解できる生徒もいるだろうが、理解が難しい生徒もいるだろう。そうした生徒に対して、図を用いた説明によって、理解が進むことを教師は期待しているのである。実際、図によってより良く理解できるようになる生徒もいるだろう。あるいは、教師は最初からヴェン図を示して、「これが共通集合だ」と教え、それを見て聞いた生徒が、「共通集合とはAとBの両方の要素になっているもののすべてからなる集合のことなのですね」と、共通集合という概念を発見することもあるだろう。ヴェン図を用いる目的がこのような効果(理解の促進や自発的な発見)を期待してのことであれば、我々が先に構成したヴェン図がその役目を担えないことは明らかである。この場合、高校の数学教科書のヴェン図は他の仕方で理解されなければならない。以下、目的をこのように仮定した上で、それにふさわしい新たなヴェン図の意味を探って行きたい。
高校の数学の教科書には、集合を表す方法として次の二つがあると書かれている。一つは要素を書き並べる方法で、「{2、4、6、8、10、12}」や「{3、6、9、12}」といった記号列で集合を表す方法である。もう一つは、集合の要素が満たすべき条件を書く方法で、「{x|xは12以下の2の倍数}」や「{x|xは12以下の3の倍数}」などの記号列で集合を表す方法である。これらはどちらも集合を記述することによって表したものである。しかし、もう一つ別の方法もある。それは集合を任意の記号列で命名し、以後、その名前としての記号列を使って集合を表す方法である。例えば、「{2、4、6、8、10、12}をAとする」や「B={x|xは12以下の3の倍数}」といった規約で集合に「A」や「B」という任意の名前を与え、以後、これらの名前によってこれらの集合を表すのである。実際、この方法は教科書でも特に断ることなくあからさまに用いられている。この方法の重要な点は、名前は任意の記号列で構わないという点であり、「A」や「B」の代わりに「C」や「D」を用いても構わない(もちろん、既に意味を有している記号列は除く)。集合に名前を付けるということは、集合演算の結果である集合に対しても行うことができる。例えば、教師は生徒に対して、「AとBの両方の要素になっているもののすべてからなる集合をCとする」と言うことができる。「AとBの両方の要素になっているもののすべてからなる集合」という記述句は長いので、「AとBの共通集合」や「A∩B」という短い記述句も導入される。後者を使えば、教師は命名規約を「C=A∩B」と簡潔に与えることができる。名前は「C」ではなく「D」でも「E」でも何でも構わない。さて、この命名規約を聞いた生徒がその意味を理解できるためには、命名されている集合が何であるのかを理解していなければならない。すなわち、それが{6、12}であることを理解できた生徒は、この集合のことを「C」と呼ぶのだということを理解することができる。しかし、「AとBの両方の要素になっているもののすべてからなる集合」という長い言い回しがうまく飲み込めなくて、それがどの集合を指しているのか理解できなかった生徒がいたとしよう。教師がこの生徒に先の命名規約を教えても実質的なことは何も伝わらないであろう(二つの記号が交換可能だということしか伝わらず、その二つが同一の何を指しているのかという肝心なことは伝わらない)。この生徒の、AとBの両方の要素になっているもののすべてからなる集合についてのぼんやりとした理解が明瞭なものになるということもない。さらに、次のような状況を考えてみよう。すなわち、教師が、「共通集合」や「∩」の意味を一切説明することなく、いきなり「AとBの共通集合をCとする」ないし「C=A∩B」と生徒に教えるという状況である。どんなに優秀な生徒でも、「共通集合(A∩B)とはAとBの両方の要素になっているもののすべてからなる集合のことなのですね」という発見をすることはあり得ない。「『C』は何を指すのですか」という質問が返ってくるだけであろう。
我々が図13に集約される形で行ったことは、基本となる集合と集合演算の結果である集合に対して任意に名前を付けたことに他ならない。
図13
ただ、「C」、「D」、「E」といったアルファベットではなく、図形を名前に用いただけである。我々はAとBの共通集合の名前として図28を用いたが、図29や図30などでも良かったのである。
ヴェンの方法に従って作図したのも、ちょうど必要な個数の図形を簡単に用意してくれるからであって、労を厭わないのであれば、必ずしも従う必要はない。例えば、図31のような図形を用意し、丸を全体集合、四角を空集合、三角を集合A、六角形を集合B、そして、星形をAとBの共通集合の名前としても良かったのである。
図31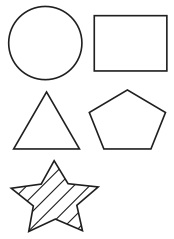
このような任意に選ばれた図形が共通集合という概念の理解を助けたり発見に導いたりすることがないことは、任意のアルファベットを用いたときにそうではなかったのと同様である。
ここで、高校数学教科書でのヴェン図による集合の命名は、完全に任意に行われているのではなく、だいたい次のような規則に従って行われているのではないか、と言われるかもしれない。
規則1:長方形内の任意の図形はある集合を表示する。
規則2:集合Aを表示する図形を除いた部分からなる長方形内の図形は、集合Aの要素ではないもののすべてからなる集合を表示する。
規則3:集合Aを表示する図形と集合Bを表示する図形の重なった部分からなる図形は、集合Aと集合Bの両方の要素になっているもののすべてからなる集合を表示する。
規則4:集合Aを表示する図形と集合Bを表示する図形を結合してできる図形(離れていても結合して一つの図形になると見なす)は、集合Aと集合Bのどちらかの要素になっているもののすべてからなる集合を表示する。
すなわち、長方形内に配置された基本図形が何を表示するかは、規則1により、完全に任意なのだが(ただし、全体集合の部分集合でなければならないが)、基本図形によって生み出される他の図形がどの集合を表示するのかは、規則2〜4によって決定されているのであり、恣意的に選べるものではない、と言うのである。さて、教師が生徒に「Ac∩BcとはAの要素になっていないものの集合とBの要素になっていないものの集合の両方の要素になっているもののすべてからなる集合のことだ」と言い、生徒は長い言い回しに幻惑されて良く理解できなかったとする。そこで教師が、先の規則を説明した上で、図32を提示し、「つまり、この図形が表示する集合のことだ」と説明すると、先の教師の説明を理解できるようになる生徒も出てくるであろう。
図32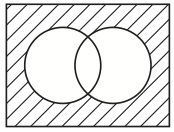
あるいは、最初に規則と図32が与えられただけで、「それはAの要素になっていないものの集合とBの要素になっていないものの集合の両方の要素になっているもののすべてからなる集合を表示していますね」と言う生徒もいるだろう。
ヴェン図を以上のような規則に支配された命名システムだと考えれば、ヴェン図の持つヒューリスティックな側面は説明できるように思われる。しかし、最も基本的なヴェン図である図33〜35のそれに関しては説明できない。
なぜならこれらの図形は規則の直接的な表現だからである。図32が生徒にとって有用であるのは、その背後にある規則を生徒は理解できているからである。
図32
「Ac∩BcとはAの要素になっていないものの集合とBの要素になっていないものの集合の両方の要素になっているもののすべてからなる集合のことだ」という説明が良く理解できない生徒でも、図32を示されることで、熟知している規則1〜4を使って、その図がどういう集合を表示しているのかを読み解くことができるのである(少なくとも、その可能性がある)。これに対して、例えば、「A∩BとはAとBの両方の要素になっているもののすべてからなる集合のことだ」という教師の説明がうまく理解できない生徒を考えてみよう。この生徒に図34が示されたとして、彼の理解は改善するだろうか。
図34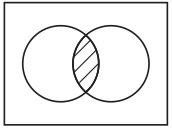
図を律している規則3には「集合Aと集合Bの両方の要素になっているもののすべてからなる集合」という言い回しがあるが、生徒に理解できないのはこの言い回しである。したがって、この生徒は規則3自体を理解できていないのである。よって、規則1〜4と図34が与えられても、この生徒は図34がどのような集合を表示しているのか読み解けない。つまり、図34は役に立たないのである。ここで、次のような反論がなされるかもしれない。図34の意味は自明である。図34がAとBの共通集合を表示していることは自明であり、図からただちに読み取れることである。そのためには規則3に頼る必要はないし、したがって、言語化された規則3を理解しておく必要もない。以上のような反論がなされるかもしれない。しかし、この反論は成り立たない。図形の重なりと共通集合の間には何ら必然的な連関がないからである。任意の図形によって集合が表示されるという規約を認めたとしても、そこから、これらの図形の重なりは共通集合を表示する、ということは論理的には帰結しない。新しい別の規約を採用して、初めてそうなるのである。この規約は完全に任意である。例えば、図34ではなく図36が共通集合を表示するというように規約することも可能であり、この可能性が先の規約の任意性を示している。
図36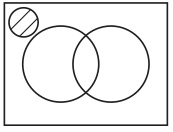
したがって、図34が与えられたら誰もが必ずそれを共通集合と結びつけるということはないのである。
高等学校の数学の教科書を見れば明らかなように、まさに共通集合、補集合、合併集合という基礎的な概念のそれぞれを説明するための補助として、ヴェン図34、33、35は用いられている。必要なのは、これらの基礎的なヴェン図の有用性も説明してくれるような、ヴェン図の意味である。
これまではヴェン図の一つ一つの図形を名前であると考えてきた。しかし、先に述べたように、集合は記述されるのが普通である。ヴェン図の図形も集合の記述と見なすことはできないだろうか。というのも、記述と考えれば、発見的有用性を説明できそうだからである。共通集合について教師が次のように補足説明したとしよう。
{x|xは12以下の2の倍数}と
{x|xは12以下の3の倍数}の共通集合とは、要するに、
{x|xは12以下の2の倍数、かつ、12以下の3の倍数}のことである。
「・・・と***の両方の要素になっているもののすべてからなる集合のことだ」という言い回しによる説明よりもかなり分かりやすくなっているように思われる。しかし、まだ言葉の理解に大きく依存しており、その点で問題を抱える学生にはあまり助けにならないかもしれない。そこで、補足説明が次のようなものだったとしよう。
{2、4、6、8、10、12}と
{3、6、9、12}の共通集合とは、要するに、
{6、12}のことである。
あるいは、黒板に次のように書いた方が良いかもしれない。
{2、4、6、8、10、12}と
{ 3、 6、 9、 12}の共通集合とは、要するに、
{ 6、 12}のことである。
こうなれば、おそらくかなりの生徒が共通集合という概念を理解できるようになるだろう。すなわち、共通集合とは何かを言語化して説明はできないかもしれないが、任意の二つの集合が要素を列挙して与えられたら、その共通集合を要素を列挙して表示することができるようになるであろう。この要素を列挙する集合の表記法は言語的というよりもむしろ図形的と言えるかもしれない。右の三つの列挙表記の二つの波括弧の部分を変形して接合して円にし、読点を省略し、数字を並び替えると、それぞれ図37〜39のようになる。
さらにこれらを重ね合わせ、図39の円だけ凸レンズ状に変形すると図40になる。
図40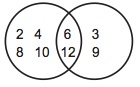
図40と同じようなものは、次のようにすれば、列挙表記法でも書けるだろう(本来は、このように書くと、6個の数の他に集合{6、12}をも要素とする集合を意味することになるので、我々がここで意図したものではなくなってしまうことに注意)。
集合の同一性はその要素によって完全に決定される。したがって、「{6、12}」は{2、4、6、8、10、12}と{3、6、9、12}の共通集合を必然的に表示している。そこには、要素の列挙によってそれらの要素からなる集合を表示するという規約を除けば、何らの恣意性も介在していない。したがって、他の規約に訴えることなく、「{6、12}」を用いて共通集合とは何かを説明することが可能である。この点が、共通集合を単なる名前で表示した場合と決定的に異なっているのである。
ヴェン図による集合の表示は要素の列挙による集合の記述方法と類似したものではないかというのが、我々がここで提案したいヴェン図の見方である。だが、ヴェン図には一般に要素が描かれていないではないか。確かに。しかし、ここで図形は点から構成されているという直観的な(数学的に厳密ではない)アイディアに訴えることができる。すなわち、ヴェン図は次のような規則によって支配されていると考えるのである。
規則0:長方形内の任意の点はそれぞれ異なるあるものを名指している(点はあるものの名前であり、異なる点が同じものの名前であることはない)。長方形内の任意の図形は、その図形を構成している点が名指しているものを要素とした集合を表示している。
「集合AとBの両方の要素になっているもののすべてからなる集合」という共通集合の説明が理解できなかった生徒でも、規則0なら理解できるかもしれない。前者の理解を困難にしている言い回しが後者には見られないからである。そこで彼は規則0なら理解できるとしよう。そして教師が、規則0がヴェン図に意味を与える根本的な規約であることを説明した上で、図44を与えたとする。
図44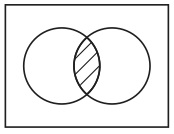
そうすると、この生徒は、図44がAとBの共通集合を表示していることを以下のように理解できるようになるかもしれない。図44を構成している点は、図41と図42の両方を構成している。
図41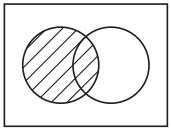 図42
図42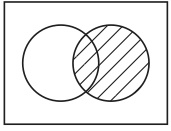
図41を構成している点はある集合(Aとする)の要素を名指しており、図42を構成している点は別のある集合(Bとする)の要素を名指している。したがって、図44を構成している点は集合AとBの両方の要素になっているものを名指している。したがって、図44は集合AとBの両方の要素になっているもののすべてからなる集合を表示している。以上のように、この生徒は共通集合というものの理解にヴェン図の助けを借りて到達できるかもしれない。同様にして、図43によって補集合の理解が助けられ、図45によって合併集合の理解が助けられることも可能性としてはあり得る。
図43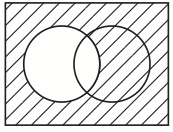 図45
図45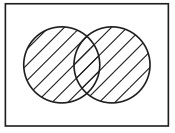
このように、規則0がその意味を与えると考えられたヴェン図は、補集合、共通集合、合併集合という基礎的な集合演算の概念の理解を助ける有用な図形となり得るのである。もちろん、高等学校の数学の教科書に現れるヴェン図が実際に規則0によって意味を与えられている図であるのかどうかは別問題であり、そうだとは断言できない。註(3)で述べたが、教科書では規則0に類するものどころか図に関する一切の説明が与えられていないからである。しかしながら、教師がヴェン図によって集合演算の結果を理解させようと意図しているならば、また、生徒がヴェン図によって実際に理解が助けられているならば、そこでは規則0かそれに類したものが、たとえ言語的に明晰に意識されることはなくても、ヴェン図の意味を与えるものとして受け入れられているのではないか、という推測は十分成り立つであろう。
規則0によって意味を与えられたヴェン図はいくつかの問題を抱えており、その結果、このヴェン図は集合演算の結果を表示することができないのではないかという疑念が生じるかもしれない。そこで、可能な限り弁護を試みておきたい。
まず、ヴェン図は要素の列挙による集合の記述方法に似ているとされるが、一般には、具体的な要素は列挙されていないではないか、と言われるかもしれない。確かに、先に見た図37〜図40のような有限集合の場合はどの点が何を名指しているかが明瞭に示されているが、一般にはそうはいかない。
例えば、2の倍数の集合Aは一つの円で表示されるが、この円を構成しているどの点が2を名指し、どの点が4を名指し、・・・、ということはまったく示されていない。この場合は、適当な方法で点と2の倍数の間に対応を設定できるかもしれないが、一般にそうできるとは限らない。例えば、人間の集合を考えてみよう。セマンティクスのレベルでも、我々は各々の人間を名指すことはできないから、当然、どの点が誰を名指すのかを書き表すことはできない。セマンティクスのレベルでは「{x|xは人間}」のように要素が満たすべき条件によって集合を記述し、{x|xは人間}の要素を点に、{x|xは人間}を点からなる図形に対応させているだけである。また、次のような批判もあるかもしれない。2の倍数の集合Aを表示している円を構成している点の個数は2の倍数の個数よりも多いと思われるが、残った点は何を名指しているのだろうか。いや、むしろ事態は逆である。紙の上に描かれた点や円は幾何学的な点や円ではなく、そこにあるのは原子(アトム)か最小可感物(ミニマム・センシビリア)か何かそういったものであり、それらが高々有限個集まっているにすぎない。その一つ一つを名前に使ったとしても、無限個ある2の倍数を名指すには足りないはずである、云々。
規則0によるヴェン図が集合を表示するためには不完全な方法であることは確かに認めざるを得ない。しかし、集合演算の結果を表示するという目的にとっては十分である、というのが以上のような批判に対する我々の回答である。ものの世界にn個の基本集合を導入すると、世界全体は2n個の最小集合に分割され(各々の基本集合は2n-1個の最小集合に分割され)、その組み合わせで22n個の集合が得られるが、そのある集合に補集合、共通集合、合併集合といった集合演算をほどこすと結果としてどの集合へ写像されることになるのかを表示することが、集合演算の結果を表示するということであった。今、世界(全体集合)として自然数をとり、n=2個の基本集合として2の倍数の集合Aと3の倍数の集合Bを導入すると、それぞれの基本集合は22-1=2個の最小集合に分割され、世界全体は22=4個の最小集合に分割される。したがって、世界が最低4個の要素を持ち、それぞれの基本集合が最低2個の要素を持つならば、世界の分割の様子を図で表し、集合演算の結果を表示することができる。この世界の分割の様子をヴェン図で表したのが図46である。
図46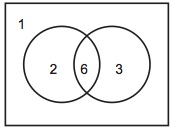
ここでは、全体集合は{1、2、3、6}、基本集合Aは{2、6}、Bは{3、6}である。数字が書き込まれた4個の図形は規則0で言われている点であることが意図されている。すなわち、「2」が書き込まれた左側の三日月状の図形は2を名指し、「6」が書き込まれた中央の凸レンズ状の図形は6を名指していると意図されている。したがって、これら二つの図形から構成される左側の円は{2、6}を表示していることになる。ところがここで一つ困った問題が生じる。我々としては凸レンズ状の図形から構成される図形で{6}を表示したいのだが、この図形は元の凸レンズ状の図形そのものであり、これは6を名指しているのであった。つまり、同じ図形があるものとそれのみを要素に含む単集合の両方の名前として用いられてしまっているのである。これは避けたいことである。そのためには、最小集合は最低2個の要素を含むと考えれば良い。そうすると、全体集合は最低22・2=8個の要素を持ち、それぞれの基本集合は最低22-1・2=4個の要素を持つことになる。ヴェン図で表すと図47になる。
図47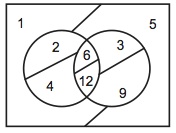
数字が書き込まれている図形が規則0の言う点であり、2個以上の点から構成された図形が集合を表示することになる。共通集合を表示するのは、「6」が書き込まれた点と「12」が書き込まれた点から構成された凸レンズ状の図形である。図47から点と点を区切る斜線と数字を消すと、通常のヴェン図である図48になる。
図48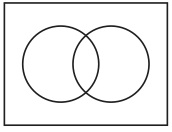
共通集合を表示する図形は図49である。
図49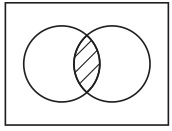
自然数も2の倍数も3の倍数も無数にあるが、有限個であると仮定しても、集合演算の結果を表示するという目的のためには問題ないのである(もちろん我々の心としては、最低の個数ではなくもっと多くの個数をイメージし、可能ならば無数の個数をイメージしたいのであるが)。また、この目的のためには、集合の要素が何であるのかを具体的に名指しして特定する必要もない。したがって、規則0によるヴェン図が要素を具体的に列挙していなくても、問題はないのである。もっと極端なことを言えば、要素として何を指定していても(例えば、2の倍数の集合Aの要素として、2の倍数ではない3を指定していても)構わないのである。集合演算の結果を表示するためのヴェン図は、2の倍数の集合Aの要素の個数が無限個なのか有限個なのか零個なのか、3はAの要素なのか否か、といったことは一切主張していない。だから、たとえ我々のヴェン図が集合Aの要素の個数を有限とし、しかも3などをその要素に含めていたとしても、間違っていると批判されるべきではない。ヴェン図はそういうことを主張しているのではなく、それをあくまでセマンティクスのレベルで仮定し、その上で、集合演算の結果を表示しているだけだからである。だが、どうしてもこのような状況は認めがたいと思う人もいるかもしれない。その場合は、集合演算の結果を表示するために2の倍数の集合や3の倍数の集合といったものを例にとるのをきっぱりとやめてしまえば良い。実際、高等学校の数学の教科書で集合演算の結果を表示するために使われるヴェン図では、集合に「A」や「B」というレッテルが貼られているが(図1参照)、それが具体的にどのような集合の名前であるのかの説明はされないのが普通である。
なぜなら、集合演算の結果を表示するという目的のためには、なんらかの特定の集合に限定して考える必要はないからである。したがって、これを無理に2の倍数の集合や3の倍数の集合などと考える必要はない。最初から、例えば、全体集合を{1、2、3、4、5、6、9、12}、Aを{2、4、6、12}、Bを{3、6、9、12}と考えれば、ヴェン図は図47のようになっていると見なすことができ、無限の問題などに頭を悩ませる必要はなくなる。
図47
集合演算の結果を表示し、集合演算の概念を理解させるためには、このようなヴェン図で十分である(12)。
最後に一つ注意しておきたいことがある。先ほど、集合演算の結果を表示するためのヴェン図は要素の個数などについての主張は行っていないと述べたが、さらに言えば、ヴェン図は集合演算の結果自体を表示しているだけであって、集合演算に関して何かを主張しているわけですらない。そうした主張は、実際には次のようになされている。
集合演算で用いられているヴェン図は、集合の名前にすぎないのであって、それ自体は何も語っていないのである。ヴェン図が何事かを語り始めるのは、別の文脈で別の目的のために使われたときである。本研究の第二論文以降では、そうした何かを語ろうとするヴェン図の検討が行われることになる。
註
(1)集合や論理の文脈を離れて、純粋に幾何学的な観点からヴェン図を考察することも可能である。例えば、A・W・F・エドワーズの『心の歯車:ヴェン図の物語』(二〇〇四)はそうした観点からヴェン図を考察した本である。そこでは、例えば、日本の日の丸の旗もヴェン図の例として挙げられている。しかし、日の丸は集合や論理の文脈で使用されているわけではないので、本研究では「ヴェン図」とは呼ばないのである。
(2)小学生と高校生では感受性も記憶力もまったく違うので、本論文の最初に述べたことに反し、今後はヴェン図に対してあまりなじみを持たない人が増えてくるのではないかと思われる。
(3)本橋(二〇〇三)、四八頁(本橋は「ベン図」という表記を用いているが、本論文では「ヴェン図」と表記する)。現時点(二〇一五年)において使われている高等学校の数学Iの教科書を幾冊か見てみると、確かにもっぱら集合演算の結果を表示するためにヴェン図が使われているが、どの教科書でも、二つの集合の間の包含関係を表示するためにもヴェン図が使われていることが分かる。ただし、ほとんどの教科書がオイラーの方式の図(本研究の第二論文で詳説する)を用いている(最初に述べたように、本研究ではこれも「ヴェン図」と呼ぶことにしているが、人によっては、例えば、本橋(二〇〇三)の四九頁は、これを「オイラー図」と呼んで区別している)。しかし、秋山仁ほか十三名が執筆している『新高校の数学I』(平成二十三年三月九日検定済、数研出版株式会社)だけが例外で、ヴェンの方式による図(これも本研究の第二論文で詳説する)を用いている。なお、調べた限りでのすべての教科書に関して言えることだが、そこでは「ヴェン図」という言葉は一度も使われていない(「オイラー図」という言葉も見られない)。また、ヴェン図は本文の中の適当な箇所に挿入されているだけで、図の説明は一切与えられていない。後者はヴェン図が言葉による説明を不要にするほど直観的に自明なものであるからかもしれない。しかし、そこには哲学的に興味深い問題が含まれているということが本研究で指摘したいことである。
(4)高等学校の数学の教科書では、「Xc」の代わりに「X」という記号が用いられている。また、共通集合は「共通部分」、合併集合は「和集合」と呼ばれている。ここでは本橋(二〇〇三)でも使われている、より一般的な記号と用語を採用した。
(5)もちろん、こうなることは図4と図5の導入の仕方に依存している。どのように導入するべきなのかは、本文ですぐに述べる。
(6)S・シンの『図形の論理的地位』(一九九四)は、ヴェン図の中の図形を三つに分類し、それぞれ、「基本領域(basic region)」、「最小領域(minimal region)」、「領域(region)」と呼んでいる(Shin 1994, p. 51)。我々の「基本図形」、「最小図形」、「図形」という分類と用語は、この彼女の分類と用語に倣ったものである。なお、何も形容されていない「領域」という語(我々の「図形」)は、ヴェン図の中に見られるすべての領域(図形)を指し、その中には基本領域(基本図形)も最小領域(最小図形)も含まれる。シンの著作は、名辞論理学が展開できるように整備されたヴェン図を用意し、その意味論を形式的に厳密な仕方で与えた最初の試みである。我々がここで行っていることは、名前しか持たない単純なヴェン図に対して非形式的な仕方で意味論を与えることである。
(7)「我々がなさねばならないことは、我々が次々に導入して行くことになる各々の図形が既に存在している下位区分(subdivision)[=最小図形]のすべてと一度は、そして一度だけ交わるような仕方で、我々の図形(例えば、円)を描くことだけである」(Venn 1880, p. 5)。この論文は大幅に書き換えられて、彼の著作『記号論理学』の第五章「図形的表示」となった。そこでは「必要なことは、一連の何らかの種類の閉曲線を次のような仕方で、すなわち、次々に描かれる各々の閉曲線が既に生み出されている区画(compartment)[=最小図形]のすべてと交わるようにし、かくして、区画の個数を二倍にするように、描くことだけである」(Venn 1881, p. 113)と述べられている。
(8)ヴェンおよび彼より以前にヴェン図を用いていたレオンハルト・オイラー(一七〇七-一七八三)は共に全体集合を表示するための図形を用いていなかった。彼らにとっては基本図形が置かれる平面全体が全体集合を表示しているのであって、それを特に長方形などで限定して示さなかったのである。ところで、我々は全体集合を表示する長方形の外部によって空集合を表示させたのだが、彼らはこの方法がとれないことになる。では彼らは空集合をどのように表示するのであろうか。本研究の第二論文で論じることになるが、空集合の問題が結局は彼らのヴェン図の問題点を明らかにするのである。
(9)Venn 1880, p. 7. ただし、長方形は我々による追加である。
(10)More 1959. モアは任意のヴェン図を作図する具体的な手続きを与えている。エリック・ハマーの『論理と視覚情報』にその分かりやすい説明がある(Hammer 1995, pp. 35-7)。この方法はヴェン図の対称性を考慮せず、既存の図形に新しい図形を順次追加して行くことでヴェン図を描く。例えば、長方形の中に4個の基本図形を描くときは、本文の図27になるのではなく、図26に1個の図形を追加した図50になり、5個の基本図形を描くときは、図50に1個追加した図51になる(Venn 1880, p. 8. 5番目の図形は点線で描かれている)(長方形は我々による追加)。
(11)高校数学の教科書で使われているヴェン図(本文の図1)には、図の中に「U」、「A」、「B」という文字が書き込まれていて、その点で我々の図形とは異なっているように思われるかもしれないが、そうではない。
我々の図形にもこれらの文字を書き込んでも構わない。すなわち、我々の方法では、長方形が全体集合U、左の円が集合A、右の円が集合Bを指示することが明示的に規約されているので、これらの文字を書き込んでいないのだが、見るものに規約を思い出させる目的で、余剰であることを承知の上で、念のためにこれらの文字を書き込んでも構わないのである。
(12)しかし、集合演算の結果を表示するという目的のためにはA、Bとしてどんな集合をとっても良いのかというと、そうではない。例えば、全体集合を{1、2、3、4、5、6、7、8、9、10}、Aを{1、2、3、4}、Bを{5、6、7、8}とすれば、我々が採用した方式でのヴェン図は図52となる。本文の図47のように要素を明示すると図53のようになる。
図52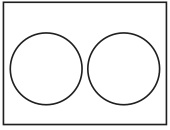 図53
図53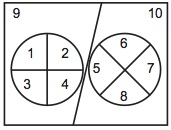
AとBの共通集合は空集合である。つまり、要素がない。よって、このヴェン図ではそれを図形として描きようがない。したがって、「ここがAとBの共通集合なのだ」と教師が生徒に直示することもできない。これでは共通集合とは何かを説明するための装置としてヴェン図が機能していないので、このような集合を例にとることはできないのである。空集合の問題は本研究の第二論文で詳しく検討する予定である。
文献
- Edwards, A. W. F. 2004. Cogwheels of the Mind: The Story of Venn Diagrams. The Johns Hopkins University Press.
- Hammer, E. M. 1995. Logic and Visual Information. CSLI Publications.
- More, T. 1959. “On the Construction of Venn Diagrams”, The Journal of Symbolic Logic 24: 303-4.
- Shin, S. 1994. The Logical Status of Diagrams. Cambridge University Press.
- Venn, J. 1880. “On the Diagrammatic and Mechanical Representation of Propositions and Reasonings”, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, S. 5, Vol. 9, No. 59: 1-18.
- ------ 1881. Symbolic Logic. MacMillan. 2nd edition, 1884. References to the latter.
- 本橋信義、二〇〇三、『集合序説』、培風館。
Set Operations and Venn Diagrams
Kouji Hashimoto
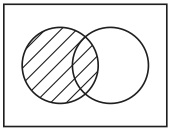
Venn Diagrams are used for several purposes. One of them is to represent the result of a set operation such as intersection, union, or complement. For example, in the Venn diagram
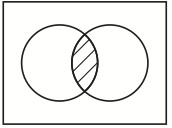 ,
,
the shaded lens represents the intersection of the set A represented by the left-hand circle and the set B represented by the right-hand circle. However what makes the lens represent the intersection is not clear. If the left-hand circle is the arbitrary name for a set A and the right-hand circle is the arbitrary name for another set B, then there is no logical reason to regard the lens as representing the intersection of the set A and the set B. It is logically possible for us to adopt not the lens but another figure, say, the left-hand lune as the name for the intersection. But many of us surely feel that it must be the lens that represents the intersection. Therefore I argue that a figure in Venn diagrams should be considered not to be a name but to be a kind of description. A figure consists of points. So suppose that each point uniquely refers to a thing in the universe of discourse and that the figure itself represents the set of all x’s, such that x is referred to by a point in the figure. Then it follows that the lens represents the set of all things that are elements of both the set A and the set B, i. e. the intersection of A and B.
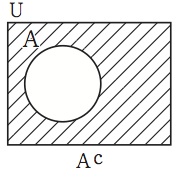
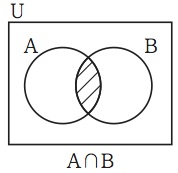
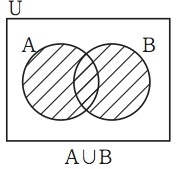









 図4
図4 図5
図5

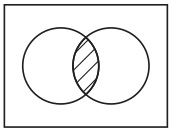 図10
図10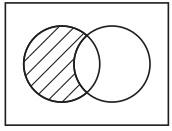 図11
図11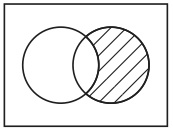 図12
図12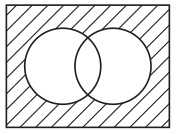










 図22
図22
 図24
図24





 図29
図29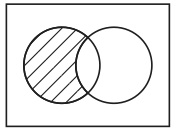 図30
図30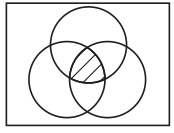


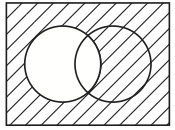 図34
図34 図35
図35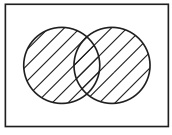



 図34
図34 図35
図35
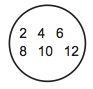 図38
図38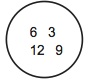 図39
図39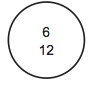


 図42
図42
 図45
図45
 図38
図38 図39
図39 図40
図40








 と
と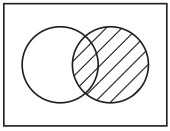 の共通集合は
の共通集合は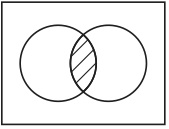 である。
である。
 図27
図27 図50
図50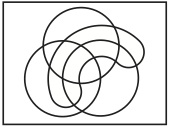 図51
図51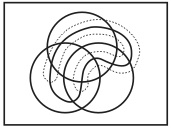



 図53
図53
 ,
,