数学的図形における真理と虚偽
橋本康二
一 序
ウィトゲンシュタインは文は図形であると考えた(1)。仮にこの考えが正しいとしたら、文であることの本質の一つは真偽になり得ることだから、図形もまた真偽になり得なければならないことになるが、果たしてそうなっているのだろうか。この疑問に対しては、一般に、図形が真偽になり得るのはむしろ当たり前であるという答えが返って来るのではないかと思われる。すなわち、真偽は本来、図形が持つ性質であり、文はある種の図形であることを通して、真偽になり得るという性質を獲得しているに過ぎないのだ、という答えである。これは真理対応説の背景にある考えである。真理対応説は、文が真になるのは文が事実に対応しているときであり、対応していないとき偽になると考えるが、これは、図は事実を正しく描写したり間違って描写したりするということをモデルにして、文の真偽を考えているのだと思われる。真理対応説が多くの人にとって魅力的で説得的であると映るのは、図形が真であったり(正しかったり)偽であったり(間違っていたり)するのは常識だと考えるものが多いからであろう。本論文の目的はこの常識を疑うことにある。
図形は真偽になり得ないということを一般的に主張するためには、あらかじめ図形とは何かを明確に規定しておく必要があるが、それは困難な作業である。そこで本論文では、まず数学的な事実を描写していると見なされている図形に的を絞り、そのなかでも典型的と思われる図形をいくつか取り上げて、少なくともそれらの図形は真偽になり得るという性質をもっていないのだと論じたい。
二 数学的事実を描写している図形
我々が取り上げるのは、数学的事実を描写していると思われるタイプの図形である。図1を見てみよう。
図1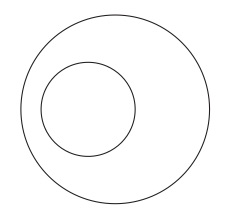
これはヴェン図と呼ばれる図形の一つであり、その一般的な理解に従がえば、これは小さい円が指示する集合が大きい円が指示する集合に包含されていること、つまり、前者が後者の部分集合であることを描写していることになる。ここで、小さい円は私の哲学の授業の履修者の集合を指示し、大きい円は私の論理学の授業の履修者の集合を指示しているとしよう。もしも、哲学を履修しているのが花子と太郎の二人で、論理学を履修しているのが花子と太郎と次郎と桜子の四人だとすれば、前者は後者に包含されているから、この図は事実を正しく描写していると言えるだろう。しかし、もしも論理学の履修者が花子と次郎と桜子の三人だとすると、前者は後者に包含されておらず、事実を間違って描写していると言えるだろう(2)。そうすると、この図は真偽になり得るということになる。しかしながら、ヴェン図にはこれとは異なる別のより自然な理解の仕方がある(3)。先の理解では、円はまず性質(いわゆる内包)を指示し、それを介して、その性質を満たすものの集まり(いわゆる外延)としての集合を指示していた。これに対して、別の理解では、ヴェン図にはそれを構成する基本的な要素図形があり、これがものを指示し、要素図形が結合してできた複合的図形は、要素図形が指示するものを要素とする集合を指示すると考える。そして、ある複合的図形の全体が他の複合的図形の部分となっているとき、前者が指示する集合は後者が指示する集合に包含されているということをヴェン図は描写していると考えるのである。この理解で図1が描かれていると考えると、それは例えば次のようになっているのである。まず要素図形として図2〜図5を準備し、これらは順に、花子、太郎、次郎、桜子を指示していると約定する。
次に、図2と図3が結合してできた複合図形が図6であり、これは花子と太郎を要素とする集合{花子、太郎}を指示している。
図6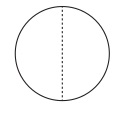
最後に、図6に図4と図5を結合させた(つまり、図2〜図5を結合させた)複合図形が図7であり、これは花子と太郎と次郎と桜子を要素とする集合{花子、太郎、次郎、桜子}を指示している。
図7
なお、図6と図7は要素図形が分かるように点線で境界を書き込んである。図1は図6と図7に着目させるために、その二つの外周を実線で描いたものである。この図1から明らかなように、図6の全体は図7の部分となっており、このことにより図1は集合{花子、太郎}が集合{花子、太郎、次郎、桜子}に包含されているということを描写しているのである。実際、この包含関係は成立しているので、図1は真だと言えそうである。そしてこの包含関係が成立していなければ図1は偽になるはずだが、そうはならない。集合{花子、太郎}が集合{花子、太郎、次郎、桜子}に包含されていることは数学的に必然的な事実であり、包含されていないということは数学的に不可能である。最初の理解では、図は直接的には性質を指示しており、しかも何がこれらの性質を持つのかは偶然的な事実であるような種類の性質だったので、包含関係が成立している可能性と成立していない可能性を考えることができたが、新しい理解では図は集合を直接指示しており、その集合の間に包含関係が成立していれば、成立していない可能性はあり得ないのである。では、ヴェン図に対する最初の理解を少し改め、図は性質ではなく集合自体を直接指示するとしたら、この理解でもヴェン図は偽になり得なくなるのだろうか。確かに、図1の小円は性質「哲学の履修者」ではなく集合{花子、太郎}を指示し、大円は性質「論理学の履修者」ではなく集合{花子、太郎、次郎、桜子}を指示していると約定すれば、図1は真であり、しかも偽にはなり得ない。だが、今度は別の図が偽になる。図1と同じような図を考えてみよう。ただし、小円は集合{花子、太郎、三郎}を指示し、大円は集合{花子、太郎、次郎、桜子}を指示していると約定する(このように意味が違うので、この図は図1とは異なると理解してもらいたい)。そうすると、この図は集合{花子、太郎、三郎}が集合{花子、太郎、次郎、桜子}に包含されているということを描写していることになるが、実際は包含されていないから、偽である。同じように、新しい理解のもとでのヴェン図も現実には成立していない事態を描写することができ、したがって、偽になることができるのであろうか。小円が集合{花子、太郎、三郎}を指示するとしたら、それは図8のように3個の要素図形からできていなければならない(左の図形が花子、右の図形が太郎、下の図形が三郎を指示すると約定する)。
図8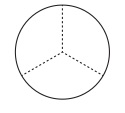
これを図4、図5と結合させると図9が得られ、これは小円が指示する集合が大円が指示する集合に包含されていることを描写していることになる。
図9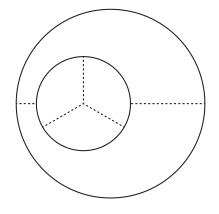
しかし、三郎を指示する図形(図8の下の図形)が大円を構成する図形にもなっているので、大円が指示する集合は{花子、太郎、三郎、次郎、桜子}であり、図9が描写しているのは集合{花子、太郎、三郎}は{花子、太郎、三郎、次郎、桜子}に包含されるということであり、実際にこの包含関係は成立しているから、図9は真である。よって、偽になることはできないのである。
新しい理解のもとでのヴェン図が偽になることはなぜ不可能なのだろうか。ヴェン図で集合間の包含関係を描写するときは、図1のように、まず大きな図形を描き、次に、その内部に完全に収まるように小さい図形を描く(つまり、小さな図形の全体が大きな図形の部分になるように小さい図形を描く)。そうすると、この小さな図形を構成している(すなわち、この小さな図形の部分になっている)任意の図形は必然的に大きな図形の部分にならざるを得ない(図10の影を付けた図形が小さな図形の任意の部分を表している)。
図10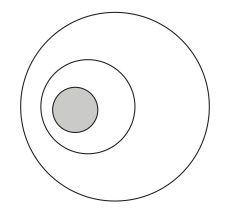
つまり、大きな図形の中に完全に収めながら、かつ、そこから部分的にはみ出すような図形を描くことは不可能である(この必然性/不可能性は平面空間における部分と全体の関係がもつ特性によるものである(4))。そうすると、現在の理解のもとでのヴェン図の図形が指示する集合はその部分となる要素図形が指示するものを要素とする集合であるから、小さな図形が指示する集合の要素はすべて大きな図形が指示する集合の要素になっている。ここで、ある集合Aの要素がすべて他の集合Bの要素になっているなら、集合Aは必然的に集合Bに包含されることになる。包含されないことは不可能である(この必然性/不可能性は集合の世界における包含関係が持つ特性によるものである)。したがって、ヴェン図が描写する集合間の包含関係は必然的に成立し、ヴェン図は必然的に真になる。偽になることは不可能である。
ヴェン図は一種のシミュレーションになっていると考えられる。すなわち、集合と図形を適切に対応付けることを通して、集合の世界で集合間の包含関係がどうなっているのかを、平面空間図形の世界で図形間の部分関係がどうなっているのかによって、シミュレートしていると考えられるのである。シミュレーションだから、どれだけ正確に対象をシミュレートできているかという問題がある。ここでの理解のもとでのヴェン図は完全なシミュレーションを行っているように見えるが、問題がない訳ではない。例えば、この理解では、要素図形が集まってできた図形は、その要素図形が指示するものを要素とする集合を指示するのであったから、要素図形が一つだけ集まってできた図形は、その要素図形が指示するもの(花子とする)ひとつだけを要素としてもつ集合、すなわち、単集合(シングルトン){花子}を指示することになる。だがそうすると、同じ一つの図形が花子と{花子}を同時に指示してしまい、多義的となる。集合の世界ではものとそのものだけからなる単集合は存在論的に区別されるのだが、平面図形の世界では、図形とその図形だけからなる図形は区別されない。この点において、平面図形による集合のシミュレーションには問題が生じる恐れがあるようにも思われる。しかし、この問題を詳しく検討する余裕は今はない。集合は2個以上の有限個の要素を持ち、集合の要素としてはものだけを考える(集合を要素とする集合は考えない)という素朴な集合間の包含関係を考える限りは、我々が考察しているヴェン図はシミュレーションとしてうまく機能しているということが認められるだろう。そこで、別の種類のより単純な数学的図形を取り上げて、そこでシミュレーションが破綻する様子を見ておきたい。
ここで取り上げたいのは、おはじきの配列によって2個の自然数の和がいくらになるのかを描写する図形である。基本になるのは、n個のおはじきが隣接して一列に並んでいると、それは自然数nを指示するという約定である。例えば、図11を見てもらいたい。
図11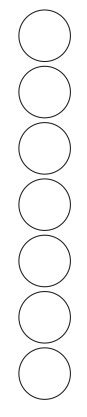
これは数7を指示することが約定されている図形である。ただし、これ自体は平面に描かれた図形であるが、実際は7個の白いおはじきが机の上に並べられている、一種の立体図形であると考えてもらいたい。同じように、図12は黒いおはじきが5個並んだ立体図形であり、数5を指示することが約定されている。
図12
次に、図13を見てもらいたい。
図13
これは、まず、任意の個数の白いおはじきを取り出して並べ、次に、やはり任意の個数の黒いおはじきを取り出して先の白いおはじきに続けて一列に並べた結果である。これは約定により数12を指示することになる。そして、それだけではなく、図13は、7+5=12という数学的事態を描写していると見なすことができる。事実、7に5を加えると12になるから、図13は真とみなせる。しかもこの事態は必然的に成立し、そうでないことは不可能であるから、図13は必然的に真であり、偽になることは不可能である。これも一種のシミュレーションであり、数の世界で成立している事実をおはじきの世界で成立する事実によってシミュレートしているのである。実際、我々が最初に算数で足し算を学ぶ時、このようなシミュレーションを通して学ぶことが多いだろう(しかも、その際、我々はそれがシミュレーションであると考えることはなく、むしろ、おはじきの世界が数の世界そのものであるとみなしている)。
このシミュレーションの欠点は、意図した計算(加算)を描写することができない点にある。図13は任意の個数のおはじきを取り上げた結果として偶然得られた図形であり、最初から7+5=12を描写しようとして作った図形ではない。そこで図形の形成方法を次のように変える。まず、7個の白いおはじきを取り出して並べる。次に、5個の白いおはじきを取り出して並べる。そして、後者のおはじきを前者のおはじきの後に移動させて、12を得る。この一連の図形の操作(図14)ならば7+5=12を描写していると見なすことができるだろう。
図14
これも先ほどのと同様、加算のシミュレーションとして問題はないようにおもわれるが、必ずしもそうではない。使用したおはじきがガラスやプラスチックなどでできていれば取り敢えず問題はないが、例えば、水銀粒がおはじきとして用いられていたとすればどうであろうか。問題ない場合もあるだろうが、時には、移動中に2個の水銀粒が接触して融合し1個になってしまうこともあるだろう。このときの図15は7+5=11を描写していることになる(他より大きな円が融合した水銀粒を表している)。
図15
7+5=11であることは不可能であるから、図15は必然的に偽であることになる。
この破綻したシミュレーションは、数を指示するために図形を用いているが、加算の描写には図形の特性はほとんど用いておらず、物質の物理的特性に大きく依存している。したがって、むしろ電卓などの機械に近いと言える。電卓は数を指示するために数字(言語)を用いているが、加算の描写(すなわち計算)には物質の物理的特性を使用している。ただし、それがおはじきの場合よりも圧倒的に複雑なだけである。物理的特性であるから、様々な物理的障害を被る恐れがある。電卓の場合、キーを強く叩いたため電子回路のハンダが剥がれて接触不良になり、最後の表示が0になってしまい、7+5=0という偽なる描写を行ってしまうということもあり得るだろう。水銀おはじきの場合、移動中の意図せぬ接触で、2個の水銀粒が融合して1個の水銀粒になってしまうという不具合が起き、7+5=11という描写を行ってしまったのである。なお、最初のおはじきのシミュレーションでもおはじきという物質を使っているのだから、水銀粒を使えば同じように故障することもあるのではないかと疑われるかもしれないが、そうはならない。7個の水銀粒と5個の水銀粒を取り出して一列に並べ、その際に、2個の水銀粒が融合して1個の水銀粒になってしまい、結果として11個の水銀粒が一列になったとしよう。おはじきの二番目のシミュレーションでは、こうした水銀粒の移動という時間変化を伴う物理的な変化の過程全体が7+5=11という描写を行なっていた。しかし、一番目のシミュレーションでは、描写を行うのは最終的に得られた水銀粒の配列だけである。そしてこの水銀粒の配列は、7+5=11という数学的に間違った事態を描写しているのではなく、7+4=11、8+3=11、6+5=11、・・・といった正しい事態を描写しているのである(最初の例では、おはじきは色分けされていたが、それは本質的に必要だったわけではなく、便宜的になされていただけであると考えてもらいたい)。このシミュレーションは、物質の持つ物理的特性に依存しているのではない。そうではなく、a個のものがあればそれは必ずb+c=aであるb個のものとc個のものから成り、d+e≠aであるd個のものとe個のものから成ることは不可能である、というある種の論理的必然性・不可能性に依存しているのである。
以上、シミュレーションが破綻する図形を見てきたが、今度は逆に、シミュレーションがより完全に行われるのはどういう図形かを検討したい。シミュレーションが完全に行われるには、シミュレートされる側とする側の両方で同じ法則が働いていることが必要であるように思われる。そこで、集合の包含関係をシミュレートする場合、同じく集合の包含関係でシミュレートしたら良いのではないかというアイディアが浮かぶ。例えば次のようにである。まず、水星、金星、地球、火星が順に花子、太郎、次郎、桜子を指示すると約定する。次に、惑星の集合はその要素である惑星が指示する人間を要素とする集合を指示すると約定する。そうすると、{水星、金星}は{花子、太郎}を、{水星、金星、地球、火星}は{花子、太郎、次郎、桜子}を指示することになる。最後に、惑星の集合の包含関係は、今述べた仕方で対応する人間の集合の包含関係を描写していると見なすのである。{水星、金星}は{水星、金星、地球、火星}に包含されている。この集合論的に必然的な事実が、{花子、太郎}が{花子、太郎、次郎、桜子}に包含されているということをシミュレートし、描写していると見なすのである。後者の包含関係も集合論的に必然的に成立しているので、この描写は必然的に真であるということになる。しかし、この方法は使えない。描写する側の集合間の包含関係は描写される側のそれと同様に五感による知覚が不可能だからである。図形による描写やシミュレーションに存在意義があるのは、目に見えないもの、あるいは、見えにくいものを明瞭に見えるようにしてくれるからである。集合は、たとえその要素が目に見える具体的な対象であっても、それ自体は五感で捉えることができない抽象的な対象であり、その包含関係を見て取ることはできない。他方、図形は目で見ることができる具体的な対象であり、その部分と全体の関係は容易に見て取ることが可能である。感覚可能であるという点で図形は文字と同じ立場にあり、したがって我々は図形を文字の代わりとしてコミュニケーションに利用することができる。しかし、集合で集合を描写したとしても、それをコミュニケーションの道具に使うことは不可能なのであり、この描写に意味はない。
そこで、数学的事実ではなく、むしろ、論理的事実と言うべきものだが、それを同じ論理によって描写している図形の例を与えておきたい。それはウィトゲンシュタインの次の主張に示唆されたものである。
「対象の同一性を、私は、記号の同一性によって表現するのであって、同一性記号の助けは借りない。対象の差異性は記号の差異性によって表現する。」(5)
同一性をめぐるウィトゲンシュタインの思想の正確な理解がここでの目的ではないので、我々はこの引用から次のようなアイディアを(独断的に)導きたい。例として金星を取り上げ、これを図16で指示することにしよう。
図16
あらゆるものは自分自身と同一であり、しかも必然的に同一であって、自己自身と異なることは不可能である。これは一種の論理的に必然的な事態である。ところで、金星もものであるから、必然的に自己自身と同一である。この事態をどのように図形で描写したら良いであろうか。いろいろな方法があり得るだろうが、ここで図16自体も一個のもの(タイプとしての図形の一つのトークンである物理的存在者)であることに注目したい(図16の代わりに例えば1個のビー玉などの立体図形で金星を指示することにすれば、それがものであることは明瞭になるだろう)。図16はものであるから、当然、金星と同じ論理に従うことになる。すなわち、図16はそれ自身と必然的に同一であり、そうでないことは不可能である。そこで、図形が自己同一的であるという事態によって、それが指示するものが自己同一的であるという事態を描写すれば良い。そうすると、図16は自己同一的であるから、それが指示している金星が自己同一的であることを描写していることになる。実際、金星は必然的に自己同一的であるから、図16は必然的に真になる。どのような図形も必然的に自己同一的であるから、それが指示するものの自己同一性を描写しており、ものはすべて必然的に自己同一的であるから、どのような図形も必然的に真になり、偽になることは不可能である(6)。
三 結論
我々は「序」で、図形は真偽になり得るという性質をもっておらず、その点で言語の文とは異なるのではないか、という疑念を表明した。この疑念は本論で確かなものとされたのだろうか。本論で取り上げられた図形は次の5種類である(一番最初に取り上げた、円が性質・内包を指示しているヴェン図は、数学的事態を描写しているとは言えないので、除外している)。
(A)図1のヴェン図(円が基本要素で、それは集合を指示する)
(B)図1のヴェン図(円を構成する図形が基本要素で、それはものを指示する)
(C)図13の数個のおはじきの列
(D)図14の数個のおはじきの列(二つのおはじきの列を結合させてできた一つの列)
(E)図16の1個の図形(ものを指示し、ものの自己同一性を描写している)
(E)は描写する側とされる側で同じ法則が支配している図形であり、(B)と(C)は、同じではないが、対応する法則が支配している図形である。これらの図形は、どれも必ず真になり、偽になることはあり得ないことが示された。この点で、これらの図形は文とははっきり区別されることになる。言語の文でも「トートロジー」とも呼ばれる論理的に真なる文は必ず真になり、偽にはなり得ない。しかし、言語の中にはトートロジーでない文も存在し、それらは当然、偽になり得る。これに対して、(E)、(B)、(C)のタイプの図形の場合、それぞれのタイプの中のどの図形をとっても、それは必ず真であり、偽にはなり得ないので、言語とは決定的に異なるのである(7)。また、これらのタイプの図形は真であることを取り敢えず認めて話を進めてきたが、果たして本当に「真」と呼べるのだろうかという疑問も生じる。真理は虚偽と対になることによって初めて意味を持ち得るように思われる。だとすると、真理しか存在しないとしたら、もはやそれは「真」と呼ぶに値しないのではないだろうか。もちろん虚偽は別のタイプの図形や言語の中には確固として存在している。したがって、それとの対比で(E)、(B)、(C)の図形も「真」として意味を持ちうるのだという考えもあるだろう。この問題に答えるためには真理・虚偽とはそもそも何なのかという一般的な問題を考察しなければならない。ここではそれを行うことはできないので、(E)、(B)、(C)の図形は真であるのだと暫定的に認めておくことにしたい。もしも真とは言えないということになったとしても、そのときは、このタイプの図形はより一層言語とは異なるということになるだけである。
次に、(A)、(D)だが、これらのタイプに属する図形の中には、真である図形もあれば偽である図形も存在する(いずれの場合も描写されているのは数学的事態であるから、必然的に真、必然的に偽、である)。そうすると、数学的図形の中には、言語と同じように真なる図形と偽なる図形の両方を含むものもあれば、言語とは違って真なる文しか含まないものもある、ということになる(8)。我々は図形とは何かを規定しなかったが、(A)や(D)のタイプの「図形」について、「これは図形ではなく、文である」と強弁することは無理だからである。本論文の観察によって確実に結論付けることができるのはここまでである。これはあまり興味深い結論とは言えないかもしれない。しかし、図形は真偽になり得ると単純に考えていたものにとっては、少なくとも幾つかの数学的図形は偽になり得ないという本論文のささやかな指摘も意義を持つだろう。
また、本論文は、数学的表象システムに新しい区分を持ち込んだという点でも意義を持つだろう。すなわち、文/図形という古い区分ではなく、真偽になり得る表象システム/真にしかなり得ない表象システム、という区分である。最後に、この区分に関して、いくつかの注意をしておきたい。
後者の真にしかなり得ない表象システムに属するのは(E)、(B)、(C)タイプの図形などであり、前者に属するのは文および(A)や(D)タイプの図形である。両者の区別の本質は、文や図形などの表象の形成が何に規定されているのかによる。後者の場合、それは一種の論理である。例えば、(B)のヴェン図の場合を考えてみよう。ヴェン図は紙の上に置かれたインクの染みなどの物理的存在であり、また、それを描くのも我々物理的な存在としての人間である。しかし、たとえ物理法則が現実からどのように変化したとしても、そこに図形が存在する限り、ある図形(例えば、図1の大円)の部分である図形(図1の小円)の部分は最初の図形(図1の大円)の部分である。よって、ここにあるのは物理的必然性を超えた一種の論理的必然性である(9)。(B)のヴェン図はこの論理的必然性によって規定された結果、真なる描写しかできないようになっているのである。(E)や(C)タイプの図形についても同様である。
他方、前者の真偽になり得る表象システムの場合はどうか。この場合も表象の形成は先と同様な一種の論理的必然性に規定されている。例えば、(D)タイプの図14で最終的に形成されたのは12個のおはじきの配列だが、これが7個のおはじきと5個のおはじきの配列ではないことは不可能である。12個のおはじきが7個のおはじきと5個のおはじきからなることは一種の論理的必然性である。しかしこのことは図14が真なる描写になることを保証してくれない。7+5=12という数学的事態を描写しているのは、図14で示された、7個のおはじきの列の後に5個のおはじきの列を移動させると12個のおはじきの列になるという物理的出来事である。したがって、これを規定しているのは様々な物理的要因と物理法則である。したがって、必ず図14のようになるという論理的な保証はなく、物理的には図15のようになることもあり得る。つまり、偽になり得るのである。
同じく前者に属する(すなわち、真偽になり得る)文はどうなっているのだろうか(10)。文は語を直線的に並べることによって作られる。例えば、集合の包含関係を描写する場合、
(17) {花子、太郎}⊆{花子、太郎、次郎、桜子}
と並べて、実際に成立している包含関係を描写することができる(「⊆」はその前に置かれた語が指示する集合が後に置かれた語が指示する集合に包含されるということをあらわす語である)。同時に、
(18) {花子、太郎、次郎、桜子}⊆{花子、太郎}
と並べることも可能である。これができないという、(B)のヴェン図に関して認められたような種類の論理的不可能性は存在しない。それは、現に右のように並べられていることから明らかである。そして、この文は成立していない包含関係を描写しているので、偽である。しかし、ここでは次のような人為的な規則が支配しているのではないかと言われるかもしれない(「Γ」と「Δ」は読点で区切られた語の有限列をあらわす)。
(19) Γの構成要素のすべてがΔにあらわれているとき、かつ、そのときに限り、「{Γ}」、「⊆」、「{Δ}」をこの順に並べよ。
確かに、この規則が完全に支配している世界ならば、有限集合の包含関係に関しては真なる文しかあり得ず、偽なる文の存在は不可能である。しかし、規則の完全な支配が成立するのは観念の世界だけである。現実の世界では、物理的な存在者としての人間がインクの染みを描いていくのであり、そこには絶対的な強制力は働き得ない。語「⊆」の意味を学んだ人間は規則(19)に従うようになる。もしも人間がチューリング・マシンに過ぎないのだとすれば、まさに電卓のようにして規則(19)に従うのであり、その場合、二節で記述したような不具合が電卓としての人間にも起こり、(17)ではなく(18)のような文字列を生成してしまうことが十分にあり得る。また、人間は単なるチューリング・マシンではなく、規則に従うことは物理的過程に完全に還元することはできない出来事であるとしても、最終的なインクの染みとしての文字列を生成する際には物理的制約を受けざるをえない。人間精神がなんらかの必然的な仕方で規則に従っていたとしても、例えば、途中でペンのインクが切れてしまえば、結果的に規則に反した文字列を生み出すことにもなるであろう。文もそれを生成する人間の内的・外的な様々な不具合によって偽になり得るのであり、その点で(D)タイプの図形と同様なのである。
註
(1)「命題[=文]は現実の像(Bild)である」(Wittgenstein 1922, prop. 4.01)。「明らかに我々は『aRb』という形の命題を像として感じている。この記号は明らかに指示されているものの似姿(Gleichnis)である」(Wittgenstein 1922, prop. 4.012)。なお、本論文では後述するように「図形」という語の意味を明確には特定しない。したがって、「像」、「絵画」などの語と区別することもしない。また、「文」は常に平叙文を意味することにする。
(2)ただし、準備中の別論文「空間的図形における真理と虚偽」において、この場合でも図1は間違っているわけではないと論じる予定である。
(3)この理解の仕方は橋本(二〇一六)で論じた。また、この理解のもとでのヴェン図が偽になり得ないことは橋本(二〇一七)で論じた。したがって、以下の叙述はこれらの論文と部分的に重なっているところがある。
(4)部分と全体の関係を扱う論理であるメレオロジーが言う推移性の公理が平面図形では成立しているということである。
(5)Wittgenstein 1922, prop. 5.53.
(6)ウィトゲンシュタインは本文で引用した命題に対する直接の注釈として、「私はそれゆえ『[f(a, b)&(a=b)]』ではなく『f(a, a)』(ないし『f(b, b)』)と書く。そして、『[f(a, b)&(a≠b)]』ではなく『f(a, b)』と書く」(Wittgenstein 1922, prop. 5.531)と述べている。つまり、彼は、そもそも対象の自己同一性について述べているのではなく、タイプとして同一の二つの記号は同じ対象を指示し、タイプが異なる二つの記号は違う対象を指示するべきであるという、言語の意味論的規則について述べていると解される。したがって、我々が本文で与えた考えはウィトゲンシュタイン解釈としてはおそらく間違っているだろう。このことは繰り返し断わっておきたい。
(7)これに関しては橋本(二〇一七)で詳しく論じたので、参照してもらいたい。
(8)(A)、(B)、(C)、(D)、(E)はそれぞれ独自の構文論と意味論を備えた別々の表象システムであり、我々はここでその各々を我々の通常の言語(真なる文と偽なる文を共に含んだ言語)と比較しているのである。(A)〜(E)を一括して「数学的図形」と称して、それを言語と対比させているのではない。(A)および(D)は、それぞれの内部に真と偽の両方の図形を有しており、それぞれが単独で言語と類比的であると我々は主張しているのである。
(9)どうしても論理的必然性とは認めたくないという考えも理解できる。その場合は、ここにあるのは超物理的必然性であると考えて欲しい。
(10)(A)タイプの図形はほぼ文と同様だとみなして良い。ただし注意が必要である。小円は集合{花子、太郎}を、大円は{花子、太郎、次郎、桜子}を指示していると約定したとすると、大円の中に小円を描くことで(本文の図1)、{花子、太郎}は{花子、太郎、次郎、桜子}に包含されるという実際に成立している事態を描写することができる。しかし、{花子、太郎、次郎、桜子}は{花子、太郎}に包含されているという実際は成立していない事態を描写すること、すなわち、偽なる描写をすることはできない。なぜなら、(平面上で)小円の中に大円を描くことは論理的に不可能だからである。だが、小円は{花子、太郎、次郎、桜子}、大円は{花子、太郎}を指示すると約定し、大円の内部に小円を描き込めば、先の成立していない事態を描写でき、これは偽になる。つまり、通常の言語では、語の意味が確定していることを前提して語を並べて文を作り、何事かを描写するのに対して、(A)タイプの図形で何かを描写するときには、まず図形が何を指示するのかの決定から始めなければならないのである。この点で(A)タイプの図形は文とは異なるが、しかし、結果としての両者の描写能力は同じである。もっとも、(A)タイプの図形を少し改良して、文と同じようにすることができる。すなわち、図形の内部に図形を配置することで包含関係を表すのではなく、例えば、図20のように左右に配置することで、左の図形が指示する集合は右の図形が指示する集合に包含されるということを描写するようにすれば良い。
図20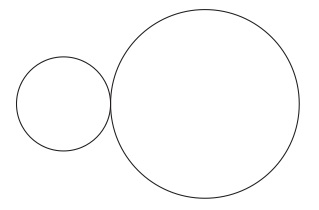
そうすると、大円が指示する集合が小円が指示する集合に包含されるということを描写したいときは、小円のなかに大円を描き込むという不可能なことをするのではなく、図21のように大円を小円の左に配置すれば済む。
図21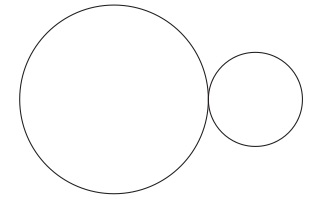
さらに改良を進めて、特別な図形を導入することで包含関係をあらわすこともできる。図22を見てもらいたい。
図22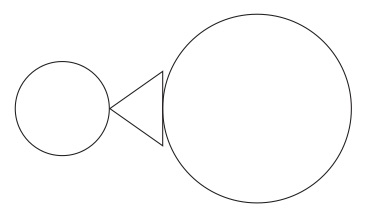
横になった三角形が包含関係をあらわしており、全体は、三角形の頂点が接している図形(ここでは小円)が指示する集合は三角形の辺に接している図形(ここでは大円)が指示する集合に包含されているということを描写している。しかし、ここまで来ると、これを文と区別して図形だと言い張ることに意味はないように思われる。
文献
- Wittgenstein, L. 1922. Tractatus Logico-Philosophicus. Routledge and Kegan Paul.
- 橋本康二、二〇一六、「集合演算とヴェン図」、『哲学・思想論集』四一号、一―二六頁。
- ―――― 二〇一七、「ヴェン図は何かを語るのか? ――『論理哲学論考』的観点からの言語哲学的考察――」、『哲学・思想論集』四二号、一―三三頁。
Truth and Falsehood in Mathematical Diagrams
Kouji Hashimoto
According to Wittgenstein in his Tractatus Logico-Philosophicus, a sentence in our natural languages is a picture of a reality. Since a sentence is essentially a truth-bearer, a picture must also be a truth-bearer. The correspondence theory of truth seems to be based on the idea that a picture is a truth-bearer. However, the mechanism by which a picture becomes a truth-bearer is not clear. In this paper, we show that at least certain types of picture or diagram cannot be false. For example, the picture of white marbles and black ones which are arranged in a line:
○○○○○○○●●●●●
can be considered to represent the true mathematical fact that 7+5=12. Moreover, the picture of any arrangement of marbles in the same way must be a true representation of mathematical sum, namely, it cannot be false. We examined the reason why certain types of picture cannot be false and other types of picture can be false.


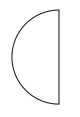 図3
図3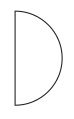 図4
図4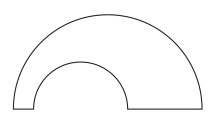 図5
図5