ジョン・ヴェンのヴェン図


橋本康二


一　はじめに

　ヴェン図はその直観的な分かり安さから、論理学や集合論を説明する際に、今日でも広く使われている。しかし、それが厳密にはどういうものであるのかは必ずしも明瞭ではない。図であるからには何かを描いているはずだが、一体何を描いているのかが、よく分からないのである。この論文では、ヴェン図とは何かを明らかにする連続研究（1）の一環として、次の問題を検討したい。すなわち、ヴェン図の創始者であるジョン・ヴェン（一八三四―一九二三）自身は、ヴェン図をどのような種類の図形と考えていたのか、という問題である。ヴェン図をどのような種類の図形と見ることができるのかという問題は、別の研究（2）で、ジョン・ヴェン自身の意図とは関係なく、考察したので、ここでは、ジョン・ヴェンに立ち返って、彼自身の本来の見解を検討したいのである。ジョン・ヴェンのテキストには、いくつかの異なった考えが見られるというのが、ここで明らかにしたいことである。

二　論理学における命題の三種類の意味

　ジョン・ヴェンは、『記号論理』（3）の第五章「図形的表象」でヴェン図を導入するのだが（4）、それに先立つ第一章「命題の諸形式について」において、論理学が扱う命題の意味を論じている（5）。この議論を知っておくことは以下でのヴェン図の考察において不可欠なので、まずこの第一章の議論を見ておきたい。
　世界には複数の物が存在し、各々の物はいくつかの性質を有しているが、それ以外の性質は有していない。これが世界のあり方だが、この世界を命題で記述するにはいくつかの方法がある、というのがジョン・ヴェンが第一章で問題にしていることである。単純に考えれば、世界がそのようなものであれば、まさに物による性質の所有の有無を、例えば、以下のように記述するのが命題であるということになるだろう。

ところが、伝統的論理学では、こうした命題（いわゆる単称命題）は基本的に扱わず、物を量化して記述する命題をもっぱら扱っている。歴史的に見て、この量化の仕方に三段階が認められ、三種類の命題が現れたというのが、ジョン・ヴェンの主張である。
　まず最初に現れた種類の命題は述定という見方に導かれて作られた命題である（6）。これは、まず、ある性質Aを取り上げる。次に、Aを持つ物のある集まりを考え（これが量化するということ）、その集まりをつくる個々の物に関して、それが別の性質Bを持つか否か、すなわち、Bがそれに述定されているか否かに着目する。そして、このことを記述するのが、この見方では、論理学の命題とされるのである。Aを持つ物の集め方には、そのすべてを集めるという方法と、そのいくつかを集めるという方法の、二種類の方法がある。これを肯定と否定と組み合わせると、この見方のもとでは命題は四種類になる。それを通常の言葉で表現すれば、次のようになる（先頭のカッコ内の英大文字はそれぞれの命題の伝統的な呼称である）。
これはアリストテレス論理学で取られている命題観である（7）。最初に見た単称命題と比較すると、主語の部分が量化されているが、述語の部分は同じであることがわかる。依然として、性質が物に述定されているというのが、世界の基本的な事態であり、この事態を主語に性質語を述語付けることによって記述するのが、基本命題である。
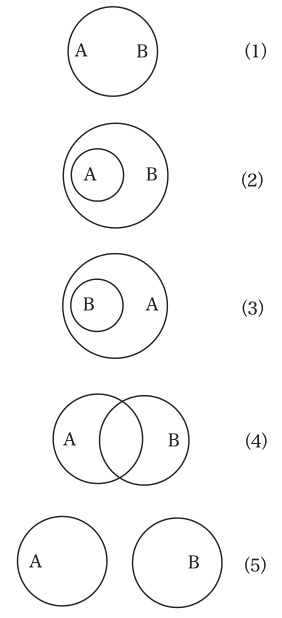
　次に現れた種類の命題は、クラスの包含・排除という見方に基づいて作られた命題である（8）。これは、まず、任意の二つの性質AとBを取り上げ、Aを持つすべての物のクラス（集まり）とBを持つすべての物のクラスを考える（つまり、両方とも量化する）。そうすると、ふたつのクラスの間に包含や排除という関係が成立することがわかる。述定ではなく、このクラス間の関係を記述するのが、この見方のもとでの論理学の基本命題である。ふたつのクラスの間の関係がどのようなものでありえるのかは、オイラー図形を描けば明瞭になる。オイラー図形は、性質Aを持つ物はすべてひとつにまとめ、性質Bを持つ物もすべてひとつにまとめて、描いたものである（9）。そうすると、図1の（1）〜（5）の5種類の関係があることがわかる（10）。 これを言葉で表現すると、次のようになる（数字は図1の中の図形に付された番号と対応している）（性質Xを持つ物すべてからなるクラスも「X」と呼ぶことにする）。
ただし、これは非常にテクニカルな表現に過ぎない。普通の言葉で言えば、順に、次のようになる。
ここで使われている「である」は物への性質の述定を言い表すための言葉ではなく、クラスとクラスの同一性を言い表している言葉である。また、「いくつかの（ある）」は真部分を意味し、決してすべての物を意味することはないと約定しておく必要がある。この命題観を取ったのはウィリアム・ハミルトン（一七八八―一八五六）である（11）。
　最後に現れた種類の命題は「コンパートメント」という見方に基づいて作られた命題である（12）。これは、まず、任意にふたつの性質AとBを取りあげる。次に、それらを否定した性質、Aではない、と、Bではない、を考える。そして、それらを組み合わせて細かく分割された複合的な性質（コンパートメント）を考える。この場合の複合的性質は、「Aであり、かつ、Bである」、「Aであり、かつ、Bではない」、「Aではなく、かつ、Bである」、「Aではなく、かつ、Bではない」の4個である。そして、この各々の複合的性質に関して、それを持つすべての物を考えるのである。そのとき、そもそもそういう物が存在しない場合と存在する場合のふたつの可能性があることに着目する。この可能性を記述するのが、この見方での論理学の基本命題であり、その種類は以下のように8個である。
この命題観を最初に取ったのはジョージ・ブール（一八一五―一八六四）である（13）。

三　ヴェン図の図形的意味

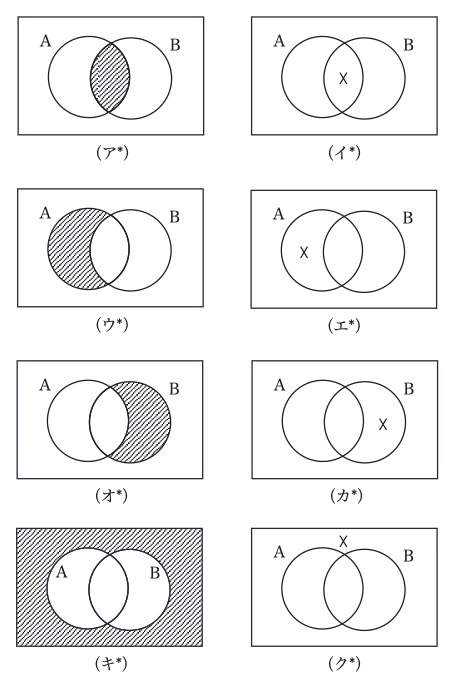
　ジョン・ヴェンが論理学の命題として採用するのは、前節の最後に現れた「コンパートメント」という見方に基づいて作られた命題である。そしてこの命題を図で表現したものがヴェン図である。前節の命題（ア）〜（ク）に対応するのが、順に、図2の（ア*）〜（ク*）である（14）。 したがって、ヴェン図が意味しているものは明白である。例えば、ヴェン図（ア*）は、文（ア）が意味しているものを意味しているのである。もちろん、文が意味するものは何かが分かっていなければならないが、それは自明である。文（ア）は、AかつBという複合性質を持つ物は存在しない、ということを意味しており、ヴェン図（ア*）も同じことを意味しているのである。
　では、ヴェン図の意味の何が問題になるのだろうか。それは、ヴェン図がその意味を意味する方法である。いったい、いかにしてヴェン図（ア*）は、AかつBという複合性質を持つ物は存在しない、ということを意味しているのであろうか。以下、三通りの可能性を取り上げて、ジョン・ヴェンがその可能性とどう関わっていたのかを検討したい。

三―一　文の単なる変形としてのヴェン図

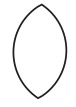
　ひとつの可能性として、ヴェン図は、普通でない語と文法を使っただけで、通常の文と本質的には変わらない、と考えることができるだろう。コンパートメント命題観における命題を表す文は、ひとつの主語とひとつの述語を順に連結することによって構成されている。ヴェン図は、主語として文字の代わりにさまざまな閉じた図形を用いる。例えば、（ア）の主語「AかつBである物」の代わりに図3の凸レンズ状の図形を用いる。 また、（ア）の述語「が存在しない」の代わりに図4の斜線を用いる。 そして、（ア）では主語の後に述語が置かれることで文が構成されているが、ヴェン図では、図5のように、ふたつの図形を重ねることで、文の代わりとなるものが構成されるのである（斜線は図形からはみ出ないように重ねる）。 この解釈では、ヴェン図（ア*）の中心にある図5は通常の文（ア）を一定のルールで変形しただけだと言える。したがって、ヴェン図（ア*）は、文（ア）の変形物であることによって、文（ア）が文に固有の仕方でその意味を意味するように、それと同じ仕方で同じ意味を意味していると見なせるのである。もちろん、文に固有のその意味作用の方法が解明されるべき問題として残っているが、それは文の問題であって、ヴェン図に特有の問題ではないので、ヴェン図の考察では問題にしないでおくことができる。
　では、なぜ、このような変形物を導入する必要があるのだろうか。それは、変形前の通常の文よりも変形後の図形の方が容易に描けるからである。ジョン・ヴェンがヴェン図を導入する際には、まさにこの描きやすさが動機となっている。ジョン・ヴェンは、コンパートメント命題観における命題は（ア）〜（ク）のように普通の言葉で表現できることを認めた上で、次のように言う。 そして、（ア）〜（ク）に代わって、主語も述語もすべて記号で置き換えた次のような記号列を使うことを提案する。 ここでは、「Aである」のような性質を表す語が「A」などの一文字に置き換えられ、「Bではない」のような性質を否定した語が「B」のように棒線を置いた文字に置き換えられている。そして、「物が存在しない」は「=0」、「物が存在する」は「>0」に置き換えられている（16）。（ア）〜（ク）よりも（ア’）〜（ク’）の方が書くのが簡単であることは明らかであろう。しかし、この記法にも問題があることをジョン・ヴェンは指摘する。単一の命題を書くことに問題はないが、それを必要十分なだけ全部書くのは大変だ、というのが彼が指摘する問題である。2個の性質を考えたとき、考慮しなければならない複合性質（コンパートメント）は4個であり、場合によっては、そのすべてに関して、それを持つ物が存在するか存在しないかを言う必要が出てくる。その場合、、複合性質の部分だけに注目すると、「AB」、「AB」、「AB」、「AB」の4個を書かなければならない。性質が「A」、「B」、「C」の3個になると、複合性質は「ABC」、「ABC」、「ABC」、「ABC」、「ABC」、「ABC」、「ABC」、「ABC」の全8個と倍増し、網羅的に書くのが難しくなってくる。 そして、この事態を解決するのがヴェン図なのである。ヴェン図はひとつの性質をひとつの図形が表すのだが、その図形の描き方に特徴があり、すべての複合的性質を効率的に描いていくことができるようになっている。それは次のとおりである。まず、平面を二分する曲線を描く。この曲線の内部の図形でひとつの性質を表し、外部の図形でその性質の否定を表すと規約する（図6は、どの図形がどの（記号列で表された）性質に対応しているのかを線で結んで示している）。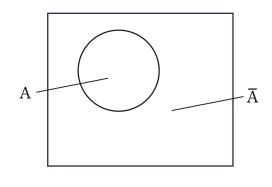 そうすると、一筆で2個の（複合）性質を描くことができる。次に、別の性質を表すためには、平面を二分する別の曲線を描くが、このとき、既にある図形のすべてを二分割するように描く。そして、最初の図形の内部にあり二番目の図形の外部にある図形は、最初の図形が表す性質と二番目の図形が表す性質の否定からなる複合性質を表す、というように規約すれば、二筆で4個の（複合）性質を描くことができる（図7参照）。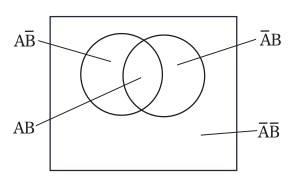 さらに第三の性質を表すために、平面を二分する別の曲線を先と同様な仕方で（つまり、すべての図形を二分するように）描き、図形と複合的性質の対応も以前と同じように定める（図8参照）。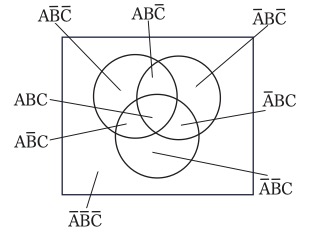 そうすると、三筆で8個の複合性質を描くことができる。ここまで来ると、ヴェン図のほうが記号列よりもはるかに簡単に、しかも正確に複合性質のすべてを列挙して描くことができることが見て取れるであろう。ジョン・ヴェンは自分で実際に試してみた結果として、次のように述べている。 このように、命題を効率的に書くためにジョン・ヴェンがヴェン図を導入したのは間違いないだろう。しかしながら、ここからヴェン図は普通の文やその記号的表記と同じ仕方で意味しているのだということは、残念ながら、必ずしも帰結しない。ヴェン図は独特の仕方で意味作用を行うのだが、普通の文とたまたま構造的に対応しており、同時に、描きやすくもある、ということは十分あり得るからである。

三―二　ヴェン＝オイラー説

　性質Aを持つ物も性質Bを持つ物も現実には世界の中に散らばって存在しているが、同じ性質を持つ物どうしを空想の中で集めて、その状態を絵に描いたのが、前節の図1で見たオイラー図形である。これは、日常言語の文の述語の部分を図形に置き換えただけとも言える。例えば、図1の（2）は、「クラスAはクラスBに包含されている」の述語「・・・は・・・に包含されている」を入れ子状態になった2個の円で置き換えていると見なせる（「クラス」という語は図では省略されている）。しかし、それは述語を他の言葉で置き換えただけということとは決定的に異なっている。両者の意味作用の仕方はまったく異なっている。述語「・・・は・・・に包含されている」は、暗黙の内に形成された日本語の規約に基づいて、クラス間の包含という事態を意味しており、その規約を知らない限り、この述語が何を意味するのか理解することは不可能である。他方、入れ子状態の2個の円は、それ自体がまさに包含という事態そのものであり、自身が包含であることによって、クラス間の包含を意味しているのである。この意味関係が規約から完全に自由であるかは疑問もあるが、図形の本性を探求することが目的ではないので、この点は追求しないでおく。しかし、図形が述語とは異なる仕方で意味作用を行っていることは、明らかであろう。言葉とは違い図形はまさに世界を描いているのである。このように、オイラー図形が通常の言語の文とは異なる仕方で意味作用を行っていることは認められるが、ヴェン図もそのように考えられないだろうか。つまり、ヴェン図もまさにオイラー図形にほかならないと見なすことはできないのだろうか。
　ヴェン図とオイラー図形の違いは明白である。命題「クラスAはクラスBに包含されている」が表象しているのと同じ事態を、コンパートメント命題観では、「Aであり、かつ、Bではない物が存在しない」と表象するのだが、前者のオイラー図形による表現は図1の（2）であり、後者のヴェン図による表現は図2の（ウ*）である。したがって、これだけ異なっている以上、両者が同じ仕方で意味作用を行っているとは思えない。しかし、両者を同じだと見なす方法もある。それがヴェン＝オイラー説である。ヴェン＝オイラー説は、ヴェン図を解釈する可能な方法のひとつとして私がかつて提案した説である（19）。ヴェン＝オイラー説によると、ヴェン図はオイラー図形と同じく、存在する物を、同じ性質を持つ物同士でひとまとめにした状態を描いたものに過ぎない。ただ、描き直しを行っているので、オイラー図形と異なって見えるだけで、描き直しを適切に処理すれば、オイラー図形とまったく同じになるのである。図2の（ウ*）に関してその具体的プロセスを見てみよう。図9を見てもらいたい。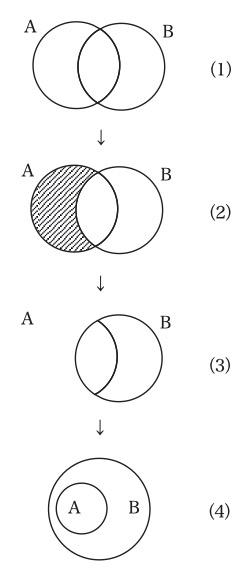 ヴェン図はまず、Aであり、かつ、Bではない物、Aであり、かつ、Bである物、Aではなく、かつ、Bである物の三種類の物がすべて存在している状態の絵を描くことから出発する（図9の（1））（20）。この状態が世界のデフォルトだからこう描いたと考えてもいいが、むしろ、最初に世界を調べたときにはこうなっていると思われてこう描いたのだ、と考えた方が分かりやすいだろう。そして、世界を調べ直したところ、先程は間違えていて、AかつBではない物は実は存在しないことが判明したとしよう。そこで、その部分に斜線を入れて消すのである（図9の（2））。これが図2の（ウ*）で、ジョン・ヴェンはこの段階で満足している。しかし、この斜線を入れて消すという方法は、あまり見栄えがしないので、鉛筆描きなら消しゴムで、ペン描きなら修正液を使って、間違えて描いていた部分を完全に消すことにしよう（図9の（3））。さらに見栄えを良くするため、同じ性質を持った物はひとまとめにして描くという方針をとったまま、少し配置を変えて描き直す（図9の（4））。これは典型的なオイラー図形である図1の（2）に他ならない。
　ヴェン＝オイラー説は、ヴェン図の斜線が入れられている部分をないものとみなすことで、ヴェン図をオイラー図形と同じものだと解釈するのだが、問題は、ジョン・ヴェン自身がこの説のように自身のヴェン図を理解していたかどうかである。この問題を考えるために、次のことに注目したい。彼は、紙に書いた二次元平面図形版のヴェン図だけではなく、木片（ピース）で作った三次元立体図形版のヴェン図も考えていた、という事実である。 ここで例に挙げられているものよりも簡単な図形として、4個のコンパートメントを持つ項が2個の図形を考えてみよう。これは図9の（1）のことである。これを板に貼り付け、ふたつの円周に沿って切り、4個のピースを作る。この状態では、見た目はもとの平面図形と大差ない。しかし、次のステップで違いが出てくる。平面図形版ヴェン図では、左側の三日月に斜線が入れられるが（図9の（2））、立体図形版のヴェン図ではこの三日月は取り除かれるのである。したがって、見た目は図9の（3）になる・・・と言いたいところだが、実際は、ふたつの円の外部に広がっている第四のピースが残っているので、図10のようになる（四角は最初に用意した板の境界である）。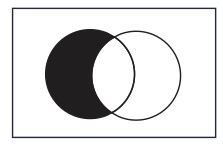 これは図9の（2）と似ているが、決定的な違いがある。図9の（2）には三日月型の平面図形がなお存在し続けているが、図10では、三日月型の立体図形（木片で構成された立体図形）はもはや存在していないのである（黒く塗られた部分は真空ないし空虚な空間だと考えて欲しい）。平面図形版ヴェン図では、存在しない物を表す図形が、斜線を入れられたとは言え、存在し続けている。これに対して、立体図形版ヴェン図では、存在しない物を表す立体図形は存在していない。したがって、立体図形版ヴェン図は、存在する図形によって存在する物を表し、存在しない物を表す図形は存在させない、というオイラー図形（図9の（3））と同じような図形になっていると見なせるのである。
　ジョン・ヴェンが、このような立体図形版ヴェン図をヴェン図の本来のあり方だと考えていたとしよう。そうすると、彼の平面図形版ヴェン図は、物理的制約によって立体図形版ヴェン図ほど図形をうまく消せないため、次善の策として、斜線を引くことで、存在しない物を表す図形を消していたのだ、と考えることもできるだろう。つまり、ジョン・ヴェンはヴェン＝オイラー説に立って平面図形版ヴェン図を描いていたことになるだろう。しかし、この可能性は確かにあるが、それほど強く主張することはできない。というのは、立体図形版ヴェン図は論理機械という特殊な文脈で持ち出されているからである。
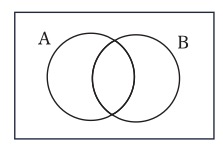
　論理機械とは、いくつかの命題が入力されたら、それらから論理的に帰結する命題を出力する機械である。ジョン・ヴェンは論理機械にあまり関心をもっていないのだが、自身の図形を基にした論理機械をいくつか考案している。そのひとつがスタンプ型論理機械である（22）。問題になっている性質の個数に応じて別々のスタンプを作らなければならないのだが、例として、最も簡単な性質が2個の場合を取り上げてみよう。この場合、インクをつけたスタンプを紙に押すと、そこには図11が描かれることになる。 これに、例えば、命題「すべてのAはBである」を入力したいならば、それは左側の三日月にペンで斜線を描くことによって実行される（図12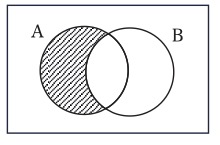）。 さらに、命題「すべてのBはAである」を入力したいなら、右側の三日月に斜線を描くことになる（図13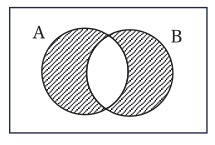）。 そして、両方の斜線を描いた後の図13自体が出力である。分かりにくいかもしれないが、そろばんとパラレルに考えればよい。そろばんの初期状態は図14のようになっているが、これに例えば数1を入力するには、上から二番目の珠を上に移動させ（図15）、続けて数2を入力するには、上から三番目と四番目の珠を上に移動させる（図16）。 この図16自体が入力されたふたつの値の和の出力になっている。なお、この出力を算用数字に翻訳すると「3」となる。同様に、論理機械の出力である図13を普通の言葉に翻訳すると、命題「AとBは合致している」が得られる（23）。
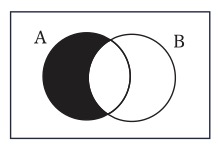
　ジョン・ヴェンが次に考案したのが、先に見た、木片を用いた論理機械である。木片の最初の配置状況は、上から眺めると、図11と同様である。命題「すべてのAはBである」の入力は、左の三日月の木片を取り去ることによって行われ（図17）、命題「すべてのBはAである」の入力は、右の三日月の木片を取り去ることによって行われる（図18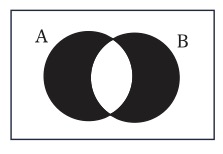）。 この図18自体が出力であり、普通の言葉に翻訳すると、命題「AとBは合致している」が出力されているのである。
　ジョン・ヴェンにとって、論理機械は、前提から結論を導く時間を短縮させるためにある。 三―一節で見たように、ヴェンの図形自体が時間の節約のために導入されたのだが、さらなる時間の節約のために、最初のヴェン図（図11）をペンで手描きする代わりに、スタンプで描いたのである。そして、節約をもう一歩すすめるために導入されたのが木片を用いた論理機械である。これはジグソーパズルのように組み直して繰り返し使用できるので、最初のヴェン図をいちいち紙に描いて準備する手間が省ける。そして、入力も、斜線を描き入れる代わりに、問題となる木片を取り去るだけでよいから、わずかとはいえ時間が節約できる。このとき、木片を取り去るのではなく、表面に斜線が描かれた同じ形をした木片に置き換えることもできたはずである。そうしても、図15の代わりに図13のような外観をしたものが得られるので、そこから図15と同様の結論を読み取ることは問題なくできる。木片の欠如としての真空も、斜線が描かれた木片も、共にそれに対応する性質を持つ物が存在しないということを意味している、ということが了解されていればよいからである。時間節約のための論理機械を考案するという文脈で木片を取り去ることにしたのは時間の節約のためだった、と考えるのが自然であろう。
　なぜ木片を取り去ることにしたのか、もうひとつ理由が考えられる。ジョン・ヴェン自身が明言しているように（25）、彼の木片を用いた論理機械はウィリアム・スタンレー・ジェヴォンズの「論理計算盤」と呼ばれる論理機械をモデルにしている。性質が2個のときの論理計算盤は次のようになっている（26）。まず、4個の棚がついた板を用意し、それを少し斜めにして立てておく。次に、4個の木片を用意し、その表面に、それぞれ、「AB」、「Ab」、「aB」、「ab」と書いておく。ここで大文字は肯定的性質を、小文字はその否定的性質を表している（ジョン・ヴェンは否定を表すのに棒線を用いていたことを思い出して欲しい）。ジョン・ヴェンの記法と同様、二つの文字を連続させることで、複合的性質を表している（27）。この木片を先の板の最上段に並べたのが、論理計算盤の初期状態である（図19）。 命題「すべてのAはBである」の入力は「Ab」の木片を最下段に移動させることによって実行される（図20）。 命題「すべてのBはAである」の入力は「aB」の木片を最下段に移動させることによって実行される（図21）。 その結果得られた図21の最上段が出力であり、ここから命題「AとBは合致している」が読み取られることになる。このような論理計算盤とジョン・ヴェンの木片を用いた論理機械の類似性は明らかである。彼は論理計算盤の四角い木片を曲線で囲まれた複雑な形の木片に置き換えただけである（28）。ジョン・ヴェンは入力のときに木片を別の箇所に移動させたが、それはジェヴォンズが木片を最下段に移動させたのにならってのことだと考えられるのである。
　しかし、時間の節約のために行ったのであれ、あるいは、ジェヴォンズの方法にならって行ったのであれ、その結果、偶然にもジョン・ヴェンが自分の本来の図形として考えていたもの、すなわち、オイラーの図形（存在しない物を表す図形は存在させないという方針で描かれた図形）に行き着いたのだ、という可能性はどこまでも残る。したがって、以上の指摘だけではヴェン＝オイラー説を完全に否定することはできない。ここで結論できるのは、木片を用いた論理機械をジョン・ヴェンが考案していることは、ジョン・ヴェンがヴェン＝オイラー説に立っていることの証拠とみなすには不十分である、ということだけである。

三―三　性質空間説

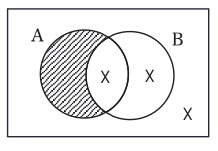
　物が性質を有するとはどういうことなのかについて、次のように考えることも可能である。すなわち、性質とは空間的なものであり、ある物がその性質を有するということは、その物がその性質であるところの空間内に存在することである、と。ヴェン図は、このように考えられた物と性質の関係を絵画的に捉えたものである、というのがヴェン図の解釈のひとつとしての性質空間説である。具体例として、図22を見てもらいたい。 「A」と付された左の円の内部の空間が「Aである」という単純な性質を表している。また、左の円の外部の空間が「Aではない」という性質を表している。「B」と付された右の円についても同様である。さらに、左の円と右の円の重なった凸レンズ図形の内部の空間は「Aであり、かつ、Bである」という複合的な性質を表している。同様に、左の円の内部にあり右の円の外部にある左の三日月状の図形の内部の空間は「Aであり、かつ、Bではない」という性質を表しており、右の三日月状の図形の内部の空間は「Aではなく、かつ、Bである」という性質を表している。四角からふたつの円を除いた図形の内部の空間は「Aではなく、かつ、Bでもない」という性質を表している。「Aである」等の性質自体が空間的なものと考えられているので、それらの性質は、このように紙の上の左の円の内部等の空間によって、絵画的に表象されているのである。そして、図22では、各々の図形に斜線やバツ印が書き込まれているが、これが空間としての性質の中に物が存在しているか否かを表している。すなわち、性質空間の中に物が存在している場合は、そのことを当の性質を表す図形の中にバツ印を置くことによって表し、存在していない場合は斜線で塗りつぶすことによって表しているのである。
　このように理解されたヴェン図とオイラー図形との違いをはっきりさせておこう。オイラー図形の場合、「Aである」というような性質自体は問題にされず、その性質を持つ物が問題にされる。それらは物理的に理解された世界の中では一般に散らばって存在しているが、いわば空想の世界の中でそれらを一箇所に団子状態にして集め、オイラー図形はそれを描いているのである。したがって、この団子状態の物の集まりを円で描くとき、円周だけではなく、その内部も含めた面が、物の集まりを描き出していると考えるべきである。水彩画や油絵なら、団子のような物の集まりを描き出すとき、色で塗りつぶされた円を用いることになることを思い起こしてほしい。一般にオイラー図形を描くときは線描という手法を採用しているので、円周だけしか描かれていないが、その場合でも、内部も含めた円全体が物の集まりを描き出していると理解すべきであろう。これに対して、性質空間説は、空間そのものが性質であると考える。物はその空間内に存在することで、その性質を獲得すると考えるのである（このように理解された性質は「電磁場」や「重力場」と言うときの場のようなものと言えるかもしれない）。ただし、ひとつの性質がすべての空間を構成しているわけではなく、様々な性質が、それぞれは明確な境界を持ちながら、相互に重なり合うことで、空間全体を構成しているのである。しかし、性質はあくまで空間そのものであるから、それ自体は物とは異なり、見えるわけではなく、性質間の境界も見ることができるようなものではない。しかし、境界は存在するので、それが見えたと仮定して、それを描いているのがヴェン図である。これは地図の緯度や経度の線と似たようなものだと考えられる。地球の表面は北半球と南半球というふたつの面からできているが、その境目に赤道という道が通っている訳ではない。しかし、境目が見えるものであるかのように、地球儀では赤道が描かれているのである。したがって、ヴェン図で描かれている円は、オイラー図形の円とは違って、円全体ではなく、円周だけが描かれていると考えるべきものである。それは、実際には見えない性質としての空間の境界線を描いているのである。境界線で区切られた空間内には、物が存在している場合と、存在していない場合がある。存在している場合は、ヴェン図では円の内部にバツ印を置くが、これは境界線を描く円周とは違い、可視的な対象を描いている普通の絵である。その物がどんな形であるのかは興味の対象外であるから、簡略にバツ印で描いているだけである。存在しない場合、ヴェン図の方でも円の内部をそのまま空白（真空）にしておけば良いのだが、ジョン・ヴェンは斜線を描きこむという手法をとっている。これは通常の絵画の技法ではなく、直観的に理解することは困難である。しかし、彼は、存在するか否かが不確定な状態を描くために空白を用いることにしたので、次善の策として斜線を描く方法を採用したのだと考えられる（29）。
　性質空間説は、ヴェン図を解釈する可能な方法のひとつとして私がかつて提案した説であり、そこで私は、これがヴェン図を図形として理解するためのもっとも有望な説であると考えた（30）。しかし、ここでの問題は、ジョン・ヴェン自身がヴェン図を性質空間説に立って理解していたか否かである。 　第二節で見たように、ジョン・ヴェンがブールとともに採用する命題観では、命題の主題は、物の集まりではなく、単純性質およびそれらが重なり合った複合的性質であり、こうした性質は「コンパートメント」と呼ばれていた。この語から普通に連想されるのは、仕切りによって区切られた、何かを収納する空間である（例えば、列車のコンパートメントは、壁や扉によって区切られた小部屋であり、中に人を収容できる）。したがって、ジョン・ヴェンは、性質を境界によって区切られた空間的なものとして考えていたのではないかと推測できる。また彼は、ある性質に関して、それを持つ物が少なくともひとつ存在するとき、その性質としてのコンパートメントが「占有されている」、それを持つ物がひとつも存在しないときはコンパートメントが「占有されていない」、「空虚である」と記述している（31）。こうした表現も、ジョン・ヴェンが性質を空間的なものと考えていたことを強く示唆するだろう。したがって、この空間的なものと考えられた性質、および、物による性質空間の占有／非占有をジョン・ヴェンは二次元空間としてのヴェン図によって絵画的に描写しようとしたのだ、と彼の意図を推測することはきわめてもっともらしいことのように思われるのである。
　しかしながら、この問題をこれとはまったく違う仕方で理解している人もいる。その一人が、ヴェン図を現代的な論理学の文脈によみがえらせることで大きな功績があったシン・ソンジュである。彼女はジョン・ヴェンの次の発言に注目する。 これに対してシンは次のように言う。 シンは表象される側の世界の中にあるのはクラスだけだと考え、「コンパートメント」と呼べるようなものは、表象する側の記号システムの中にある図形だけだと考えている（確かに、ヴェン図の図形は、境界線だけが描かれていて、中は空虚であり、そこにバツ印や斜線を収容することができるので、「コンパートメント」と呼ぶことができる）。ヴェン図においては、コンパートメント状の図形が物の集まりであるクラスを表象しているのである。したがって、コンパートメントがコンパートメントを表象するということは、メタ図形によって図形を表象するという特殊な状況でない限り、ありえない。コンパートメントが表象されるという考え自体がナンセンスである。このようにシンはヴェン図を理解して、先のジョン・ヴェンの発言を批判しているのである。
　ヴェン図に対するシンの理解は基本的に三―一節で見た理解の仕方と変わらない。ヴェン図は、日常言語の文や記号論理の式と同じく、表象されるもの、すなわち、物の集まりとしてのクラスと恣意的に結び付けられているに過ぎない。オイラー図形では、クラス間の関係（包含関係や同一性関係など）と図形間の関係の類似性に訴えて、後者が前者を絵画的に描写するものになっている。しかし、ヴェン図にはクラスとの間にそうした類似性は認められないから、恣意的な結び付きであると考えるのも自然かもしれない（34）。しかし、性質空間説が注目している「コンパートメント」という言葉は、表象される側にある存在者（性質）を名指すために使われているのである。確かに、ジョン・ヴェンは、図形のことも「コンパートメント」と呼ぶことはあるし（35）、先程も述べたように、ヴェン図の図形が「コンパートメント」と呼ばれるようなものであることも間違いない。しかし、ジョン・ヴェンが『記号論理学』で最初にこの言葉を用いたのは、ヴェン図が導入される第五章より前の第一章においてであり、第二節で見たように、そこでは表象される側のものが「コンパートメント」と呼ばれている（36）。ジョン・ヴェンの論理学は、物の集まりとしてのクラスではなく、このコンパートメントを主題としているのである。図形もコンパートメントという性格を有しているので、このことを利用して、ヴェン図は絵画的にコンパートメント（性質）を表象しているのだ、というのが性質空間説である（37）。したがって、なぜシンがジョン・ヴェンの言葉使いを無視して、ヴェン図で表象されるのは物の集まりであるクラスだと決めてかかっているのか、理解に苦しむのである。
　なぜこのようにジョン・ヴェンを批判するのか、シンは語っていないが、ひとつの可能性として、次のように推測することができる。ジョン・ヴェンは、もともと、オイラー図形でクラスを絵画的に表象していた。しかし、利便性等の理由からオイラー図形を少し変形したヴェン図を用いてクラスを表象するようになった。この時点で、ヴェン図はクラスを恣意的に表象する単なる記号でしかなくなっている。ところが、ここで「転倒」が生じた。すなわち、単なる記号に過ぎなかった表象する図形の持つ特性が、表象される世界の側の特性そのものであると考えられるようになったのである。その特性がコンパートメントとその占有／非占有である。かくして、性質はコンパートメント的な性格を持ち、物はこのコンパートメントを占有することで当の性質を帯びるようになる、という形而上学的な世界のあり方を前提し、ヴェン図はそれを絵画的に表象しているのだ、とジョン・ヴェンは考えるようになったのである。シンの意図は不明だが、以上のような仕方でジョン・ヴェンを批判することもできるだろう。
　性質をコンパートメントと捉えるアイディアがどのようにしてジョン・ヴェンに生じたのかは、確かに謎である。彼はそれについては何も述べていない。実際に、右の推測のような「転倒」があったのかもしれない。その場合、表象するものと表象されるものを混同した単なる誤りとして、ジョン・ヴェンの考えを正すべきかもしれない。そうすると、シンが理解したように、ヴェン図はクラスを表象する恣意的な記号ということになるだろう。しかし、この「転倒」を錯誤としてではなく、肯定的に評価することも可能である。すなわち、ジョン・ヴェンは、ヴェン図によって首尾よく世界が表象されているということから出発して、世界の構造もヴェン図と同じ様になっているはずだ、と推論したのではないか、と評価するのである。これは、例えば、「ソクラテスは人間である」という日常言語の文の主語・述語構造という特性から出発して、世界の側にもそれに対応した個物と普遍から構成された事実が存在している、と推論するようなものである。自然科学ではなく形而上学的な問題を探求しているのだから、このような普通ではない推論方法を用いているのである。このように考えると、コンパートメントを世界の側に措定したことをひとつの形而上学的仮説として認め、ヴェン図は絵画的にコンパートメントを表象しているというアイディアを、「正す」のではなく、額面通り受け取ることができるだろう。もっとも、ジョン・ヴェンが世界の側にコンパートメントを導入したことの是非は、ジョン・ヴェンはヴェン図をどのようなものとして考えていたのかを追求している現在の文脈では、棚上げしておくことができる。単なる錯誤であろうが、形而上学的推論によるのであろうが、ジョン・ヴェンがコンパートメントを導入して、ヴェン図はそれを表象しているものと考えていることは否定できない。そして、ヴェン図自体がコンパートメント的性格を持つのだから、ヴェン図はその類似性を利用して世界の側のコンパートメントを絵画的に表象していると見なすことができる。しかし、ジョン・ヴェン自身がそこまで考えていたと断言することは、やはりテキスト上の証拠がないので無理である。

四　おわりに

　ジョン・ヴェンは自分のヴェン図がどのような仕方で世界を表象しているのかを明確な形では述べていない。そこで、本論文では、彼のテキストのいくつかの記述に着目して、そこから彼がこの問題をどう考えているのかを推測した。その結果、三通りの異なる考えを取り出すことができた。三―一節では、彼は、ヴェン図は日常言語の通常の文と同じ仕方で世界を表象している、と考えている可能性を指摘した。三―二節では、ヴェン図はオイラー図とまったく同じ仕方で、絵画的に世界を表象している、と考えている可能性を指摘した。三―三節では、彼は、世界における個物と性質の関係を物による空間の占有／非占有と捉え、ヴェン図はそのことを絵画的に表象している、と考えている可能性を指摘した（三―二節の考えと、絵画的表象という点では同じだが、表象されている世界の捉え方が異なっている）。この三通りのうちのどれがジョン・ヴェンの真意であったのかは決定できない。おそらく彼はこの問題をそれほど厳密に考えておらず、文脈に応じて様々な可能性を当てはめて自由に考えていたのではないかと思われる（38）。もともと、オイラー図は名辞論理の推論を分かりやすくすることを目的としていたのであり、それを継いだヴェン図もその目的のために考案されたと考えられるから、ヴェン図がその目的にかなっている限り、ヴェン図が厳密にはどういうものであるのかという問題は、ジョン・ヴェンの重大な関心ではなかったのであろう。言語や図形と世界の間の表象関係を扱う意味論が論理学や哲学の研究対象となってくるのは、彼の『記号論理』（初版は一八八一年で、第二版は一八九四年）より後の二〇世紀になってからである。もっとも、ジョン・ヴェンは一九二三年まで生きたので、その前年に出版されたウィトゲンシュタインの『論理哲学論考』（39）を読んでいた可能性もある（彼は論理学関係の文献を大量に調査しており、一八七九年のフレーゲの『概念記法』（40）についても論じているほどである（41））。『論理哲学論考』の主題のひとつは言語と世界の間の表象関係がどうなっているかであり、それについての「像の理論（ピクチャー・セオリー）」と呼ばれる独特なアイディアをウィトゲンシュタインは提案している。もしもジョン・ヴェンが像の理論を読んでいたとすれば、自身のピクチャー（ヴェン図）のことをどう思っただろうか、というのは興味深い問題である。

註

（1）これまで、橋本（二〇一六）、（二〇一七）、（二〇二一）、（二〇二二）でヴェン図の研究を行ってきた。本論文は単独で読んでも理解できるよう、これらの研究の内容を部分的に繰り返したところがあることを、あらかじめ断っておく。
（2）橋本（二〇二二）。
（3）Venn 1881.
（4）『記号論理』の第五章は論文「命題と推論の図形的機械的表示について」（Venn 1880b）を書き直したものである。
（5）『記号論理』の第一章は論文「論理学の命題の諸形式について」（Venn 1880a）を書き直したものである。
（6）述定という見方（predication view）は、Venn 1881, pp. 3-5で論じられている。なお、「述定（predicate）」は主語と述語の関係だけではなく、物と性質の関係も意味している。しかし、日本語に訳すときは、主語と述語の関係の場合は、「語『人間』が語『ソクラテス』に述語付けられる」と言い、物と性質の関係の場合は、「人間という性質がソクラテスという物に述定される」と言うことにする。
（7）アリストテレスの『分析論前書』では、このような日常的な言い方ではなく、普通でない専門的な言い方がされている。例えば、本文で挙げた（A）命題は、「（BはすべてのAに）huparchein」という動詞を使って表現されている。この動詞を使った（A）命題は、英訳では「B belongs to every A」となっていて、日本語訳では「BはすべてのAにある」となっている。日本語訳の訳者（今井知正と河谷淳）は、「［アリストテレスがこのような普通でない言い方をしたのは］論理学における述語主義を表現することを目的としている」と述べている（『アリストテレス全集2』の『分析論前書』補注A）。ジョン・ヴェンの言い方だと、アリストテレスは自分が述定という見方で命題を捉えていることを強調しているのである、ということになるだろう。
（8）クラスの包含・排除という見方（class inclusion and exclusion view）は、Venn 1881, pp. 5-23で論じられている。
（9）オイラー図形についての詳細は、橋本（二〇二一）で論じたので、参照してもらいたい。
（10）ジョン・ヴェン（Venn 1881, pp. 6-7）によると、ふたつのクラスの関係がこの5種類になることを初めて指摘したのはジョゼフ・ディエズ・ジェルゴンヌ（Gergonne 1816-17）だということである。
（11）ハミルトンが命題として列挙しているのは（1*）〜（5*）の5種類だけではなく、もう3種類ある（Hamilton 1860, p. 277）。このことからも明らかなように、厳密に言えば、ハミルトンの命題観はクラス間の包含・排除に基づくものではなく、その萌芽的段階にあるとしか言えない。ジョン・ヴェンはそのことを詳しく論じているが、ここでは省略する。
（12）コンパートメントという見方（compartmental view）は、Venn 1881, pp. 23-28で論じられている。
（13）Boole 1847.
（14）ジョン・ヴェンはバツ印ではなく数字を用いている。バツ印（ないし数字）を用いたタイプのヴェン図には少し複雑な事情があり、それについては橋本（準備中a）で論じる予定である。
（15）Venn 1881, p. 112.
（16）コピュラも含めてすべてを記号で表した命題を用いる論理学をジョン・ヴェンは「記号論理学（symbolic logic）」と呼ぶのである（Venn 1880c, pp. 248-9参照）。記号論理学の成立に関しては坂本（二〇一九）から多くを学んだ。なお、「コンパートメント」という命題観を最初に取ったブールも命題を記号で表現しているが、彼が Boole 1847 で用いた記法はジョン・ヴェンのものとは少し異なっている。ブールは性質「x」の否定を「x」ではなく「1-x」と表している。また、性質を持つ物が存在することは「>0」ではなく「=v」で表している（「v」は不特定のクラスを表している）。
（17）Venn 1881, p. 113.
（18）Venn 1881, p. 117. ただし、新しい性質を考えるために次々に新しい曲線を導入していくと、ヴェン図は描くのがだんだん困難になってくるし、ジョン・ヴェンもそのことを認めている。ただ、実用上はそれほどたくさんの性質を考える必要はないので、その限りではヴェン図の方が便利なのである。
（19）橋本（二〇二二）の第三節において。
（20）ヴェン図はバツ印を置いた図形で存在を表すのが普通なのだが、ここでは、オイラー図形に合わせて、バツ印も斜線もない図形で存在を表すことにする（ヴェン図本来の何も置かれていない図形が必要になれば、バツ印か何か適当なものを置いた図形を用いれば良い）。
（21）Venn 1881, p. 135.
（22）Venn 1881, p. 135.
（23）図13は複数の情報を含んでいるので、命題「AとBは合致している」だけが出力されているわけではない。たとえば、トリビアルだが、命題「すべてのAはBである」が出力されているとみなすことも可能である。しかも、そろばんとは違い、出力をどのように日常言語の文に翻訳するのかの決定手続きは与えられていない。こうしたことも理由になって、ジョン・ヴェンは論理機械をあまり評価しないのである。論理機械の詳細な検討はこの論文のテーマではないので、ここではこれ以上は述べないが、ジョン・ヴェンや本文で後述するジェヴォンズらの論理機械を考察した論文として、山田欽一（一九五一）があるので、参照されたい。
（24）Venn 1881, p. 135.
（25）Venn 1881, p. 135.
（26）論理計算盤（logical abacus）は、最初、Jevons 1866で発表され、後にその記述がJevons 1869に再録された。後者には設計図と詳しい説明が追加されている。
（27）「AB」、「Ab」、「aB」、「ab」のように複合的性質のすべてを列挙したものを、ジェヴォンズは「論理ABC（Logical Abecedarium）」（Jevons 1874, p. 107）、後に「論理アルファベット（Logical Alphabet）」と呼んでいる（Jevons 1877, p. 93）。
（28）ただし、性質を表すための文字の使い方が異なっている。これは些細な違いのようにも思えるが、ある点で重要な違いをもたらすことになる。この問題については、橋本（準備中b）で詳しく見る予定である。
（29）ヴェン図における不確定性の問題は橋本（準備中b）で論じる予定である。
（30）橋本（二〇二二）の第五節を参照。
（31）「コンパートメントの占有ないし非占有（the occupation or non-occupation of compartments）」はVenn 1881では24頁が初出で、以後、同様の表現が繰り返し出てくる。「コンパートメントが空虚（empty）である、ないし、占有されている」も24頁が初出で、「空虚」も以後、ときどき使われている。
（32）Venn 1881, p. 119.［　］内は、これを引用したシンによる補足。
（33）Shin 1994, p. 20.
（34）シンと共に論理と図形の問題を研究していたエリック・ハンマーも同じような理解をしていることが、オイラー図形とヴェン図を比較した次の文章に見て取れる。「オイラー図形は、強力な視覚的比喩を利用して、集合の世界を印刷されたページに移し替えている。ある集合が空であることを主張するために、ヴェン図のように、恣意的な装置を利用するのではなく、オイラー図形は、同じことを、曲線の組合せの適切な領域を削除することによって、表現する」（Hammer 1995, p. 69）。
（35）「任意の種類の一連の閉じた図形を、既に作られていたすべてのコンパートメントを横切るように次々と描いていく・・・」（Venn 1881, p. 113）。
（36）第一章の元になった論文（Venn 1880a）でも同じように「コンパートメント」という語が使われている。この論文にはヴェン図は出てこない。
（37）コンパートメントの中に物が存在しているときは、コンパートメントとクラス（物の集まり）は同一視することが可能であり、したがって、同じ図形で描くことができる。例えば、ひとつの円は、円周で区切られた空虚な空間だと見れば、それはコンパートメントを描いていると見なすことができるし、円周の中も含めた円だと見れば、それはクラス（物が集まって団子状態になっているもの）を描いていると見なすことができる。したがって、この場合、図形が表象しているのはコンパートメントなのかクラスなのかという問を問うこともできる。しかし、コンパートメントの中に物が存在していないとき、無い物は描きようがないから、クラス（空クラス）を図形で描くことはできない（実際、オイラー図形では空クラスは描かない）。したがって、この場合に図形が与えられていれば（ヴェン図がそうである）、それはクラスではなくコンパートメントを表象していると考えざるを得ないのである。
（38）本文で取り上げたものとは異なる考え方もジョン・ヴェンは示唆している。例えば、彼は「我々に関心があるのは現実的であるか可能的であるような諸対象のクラスであり、これらのクラスは円や他の閉じた図形によって非常に適切に表象することができる」（Venn 1881, p. 138）とも述べている。これを額面通りに受け取ると、ヴェン図の斜線が入っている部分は現実には存在しない単なる可能的対象を集めて団子状態にした様子を描いている、とジョン・ヴェンは考えていたと言えるかもしれない。これは、かつて私が「可能対象説」と呼んだ、ヴェン図の理解の仕方のひとつの方法である（橋本（二〇二二）、第四節）。
（39）Wittgenstein 1922.
（40）Frege 1879.
（41）Venn 1881, pp. 491-2.

文献

謝辞

　匿名査読者からの指摘によって、いくつかの箇所で論述を改善することができました。二人の査読者に感謝します。本研究はJSPS科研費JP22K00001の助成を受けたものです。助成に関わった方々に感謝します。



John Venn and Venn Diagrams

Kouji Hashimoto


In what way did John Venn think a Venn diagram represented the world? 　There are at least three different answers. First, he may have thought that a Venn diagram represented the world in the same way as a sentence in our ordinary language did it. In this case, a Venn diagram is an arbitrary device to represent the world. Secondly, he may have thought that a Venn diagram represented the world in the same way as an Euler diagram did it. In this case, a Venn diagram is a picture of the world. Thirdly, he may have thought that a Venn diagram represented the world pictorially, but in a way that is different from Euler diagrams. It is impossible to determine which answer correctly captures his real thought because each of the answers is suggested in his Symbolic Logic.