Atomic_Logic

原子命題論理とそのメタ論理学
――女の理由のすべて――

橋本康二

1.　はじめに

　私たちの思考の流れを支配している法則が論理である。しかし、物体が物理（法則）に逆らって運動することが現実世界ではあり得ないのとは対照的に、私たちの思考は必ずしも論理にしたがって進行するわけではない。この点で論理は法律などの人為的規則と類比的である。論理にしたがって正しく思考できるようになるためには、私たちは一定のトレーニングを積む必要がある。つまり、論理は私たちが体得すべき一種の規則なのである。他方、物理（法則）を研究する学問として物理学があるように、論理も学問の研究対象となり得る。論理を探求する学問は「メタ論理学」、「メタ理論」、あるいは簡単に「論理学」などと呼ばれている。
　今日の大学の論理学の授業で教えられているのは上の意味での論理学である。ここで一つの問題が生じる。論理学を学ぶには既に論理をある程度体得しておく必要がある。しかし、とくに一般教養課程の初等論理学の受講者に対して、こうした論理的に正しく思考する十分な能力を期待することは難しいのが現状である。理想を言えば、まず最初に論理のトレーニングを必要なだけおこない、その後に論理学を教えるべきであろう。だが現実には、論理学を教える過程で同時に強引に論理を身につけさせるという、かなり無理な方法が一般におこなわれている。この方法について行くことができる受講者もいるが、ドロップ・アウトするものも多い。
　しかし、それほど高度な論理を身につけていなくても論理学の初歩を学ぶことは可能である。本論文では、きわめて単純な論理――それを「原子命題論理」と呼ぶことにする――を取り上げて、そのメタ論理学上の結果である完全性と決定可能性を示す。その証明は非常に単純であり、論理のトレーニングをあまり積んでいない者でも理解可能である。また、この理解に基づけば、より進んだ論理――命題論理、1 階述語論理、自然数論など――のメタ論理学へとスムースに進んでいくことができるであろう。このような仕方で論理学の初学者をサポートすることが本論文の目的である。

2.　論証の妥当性

　論理学は思考の法則としての論理を研究するが、思考そのものを研究対象とするのではなく、思考を目に見える形に置き換えたものとしての言語を直接の研究対象とする。私たちの一連の思考の流れは、言語的には文の列となるので、論理学は文の列を支配している法則を探求することになる。私たちはとりとめのないことを考えることが多く、それに対応して、文の列の多くにも何らの秩序も見いだせない。しかし、中には興味深い特徴を持つ文の列もある。以下のような三つの文の列を考えてみよう。

この列は、一番目と二番目の文が真ならば、三番目の文も必ず真である、という特徴を持っている。言い換えると、一番目と二番目の文が真ならば、三番目の文が偽であることは不可能である。これは注目に値する特徴である。私たちは一番目と二番目の文が真であることは知っているが、三番目が真であるかどうかは知らないとしよう。しかし、上の文の列がそこで述べたような特徴を持っていることを知っているならば、安心して三番目の文を主張することができる。それが真であることは保証されているからである。真なる文のみを作り出すことが私たちの目的ならば、これほど役に立つ特徴はない。したがって、上の文の列がこのような特徴を持つことに基づいて、次のような規則をたてることができる。

これは私たちの思考を導く規則の一つであり、すなわち、論理の一つである。
　ここで専門用語を導入しておく。論理学では、このような文の列は「論証」と呼ばれる。論証の一番最後に位置する文は「結論」と呼ばれ、それ以外の文は「前提」と呼ばれる。私たちの言語では、結論の前に「それゆえ」等の語が置かれるのが普通である。本論文では論証を書くときに次のような規約を採用する。まず、文は多くの場合アルファベットの大文字一字で表す。例えば、「人間は必滅である」は「A」、「ソクラテスは人間である」は「B」、「ソクラテスは必滅である」は「C」で表されるとする。また、結論の前には「それゆえ」等の代わりに「／∴」を置く。前提が複数ある時は、コンマで区切る。したがって、上の論証は次のように書かれることになる。

論証は、前提のすべてが真ならば結論も必ず真になるとき、「妥当な論証」と呼ばれる。前提のすべてが真で結論が偽になることが可能なら、「非妥当な論証」と呼ばれる。したがって、論理学は論証の妥当性と非妥当性を研究する学問ということになる。

3.　複数の論理

　論理学は妥当な論証を研究するにあたって、まず、なぜある種の論証は妥当になるのかを解明しようとする。論理学の考えるところでは、論証の妥当性は言語の意味によって生じる。言語がある意味を持つことによって、世界の偶然的な在り方がどうであろうとも、ある文が真ならば、しかるべき文も必ず真になる（すなわち、前者を前提、後者を結論とする論証が妥当になる）、というわけである。したがって、私たちの言語の意味を完全に明らかにすることができるならば、論証の妥当性はすべて説明し尽くされたことになり、妥当な論証全体の確定した集合が私たちに与えられたことになる。しかし、事はそう簡単には運ばない。私たちの言語の意味は圧倒的に複雑であり、この言語の堪能な使い手である私たち自身にとってさえ、その意味を完全に明らかにすることは、きわめて困難だからである。
　そこで論理学は以下のような方策をとる。まず、言語の意味を非常におおまかに捉える。そして、この意味によってある種の論証が妥当になることを示す。しかし、このように捉えられた意味は非常にアバウトであり、また、間違いを含んでいることさえある。そこで次に、言語の意味をより細かく捉えることが試みられる（間違いを修正することも試みられる）。このように捉え直された新しい意味によって、以前とは異なる種類の論証が妥当になることが示される。しかし、これも言語の意味の把握としてはまだ杜撰なところがあるので、さらに細かく意味を捉えることが試みられ、新しい種類の論証の妥当性が示されることになる。しかし、まだ言語の意味の完全な把握にはいたっていないので、さらに・・・。
　私たちの言語の意味は、私たちがそれを完全には明示できないにしても、一つに確定していると考えられる。したがって、妥当な論証もただ一種類しか存在しないはずである。いわば、論理は絶対的であり、一つしか存在しない。しかし、私たちの無知のせいで、言語の意味の捉え方は複数存在し、この捉え方のそれぞれにおいて、異なる種類の妥当な論証が存在してしまうことになる。つまりこのような方策をとる論理学研究においては、論理は意味の捉え方と相対的なものとなり、複数の論理が存在するのである。
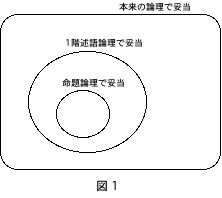
　一般的な論理学の教科書は、もっとも粗く意味を捉えた結果生じる論理を「命題論理」、それよりも細かく意味を捉えた結果生じる論理を「1 階述語論理」と呼び、この順序で論理学を展開している。「意味を捉える」、「粗く捉える」、「細かく捉える」ということがどういうことなのかは、その具体的な手続きを見るしかない。5 節と 6 節でそれを少し見ることになる。ここでは、意味の把握の相違によって生じる複数の論理の関係について、命題論理と述語論理を例に、あらかじめいくつか注意しておきたい。まず、命題論理を生み出す意味の捉え方にも確かに間違いが含まれているが、この間違いは比較的無害である。なぜなら、命題論理によって妥当とされる論証は、唯一絶対の論理（すなわち、私たちの言語の意味が完全に捉えられたときに明らかになる本来の意味での論理）において妥当とされる論証の一部となっているからである（このことは厳密には証明できず、そうなっているという私たちの直観を信用するしか方法はない）。次に、意味をより細かく捉えた結果得られた 1 階述語論理は命題論理を完全に内に含んでいる。つまり、命題論理で妥当な論証はすべて 1 階述語論理でも妥当であるが、命題論理で非妥当とされた論証の中には、1 階述語論理で妥当とされる論証もあるのである。図 1 で示されているように、意味をより細かく詳しく捉えて行くにつれ、それによって妥当とされる論証の集まりは、以前の妥当な論証の集まりを完全に内に含む形で拡大して行き、最終的には本来の意味での「論理」における妥当な論証の全体にまで到達することが期待されているのである。

4.　完全性と決定可能性

　言語の意味を明らかにすることによって、その意味に依存して妥当になる論証の集合が確定するのであれば、論理学の目的は言語の意味をより完全に明らかにしていくことだけであると思われるかもしれない。しかし実はそうではない。妥当な論証の集合が確定したとしても、具体的に与えられた任意の論証がその集合に属するか否かは、私たちには必ずしも明らかではないからである。意味を明らかにしたのは私たちだが、その結果どういう論証が妥当になるのかまで私たちはあらかじめ見通しているわけではない。そこで、複数存在する論理のおのおのにおいて、任意に与えられた論証がそこにおいて妥当であるかどうかを私たちはどのようにして決定できるのかが問題になる。論理学はこの問題を追求しなければならない。
　もっとも望ましいのは、ある与えられた機械的な手続きにしたがえば、どんな論証に関しても、妥当か非妥当かを正しく決定できるようになることであろう。自分自身では論理をほとんど体得していないものでも、この機械的な手続きにしたがって事前にチェックすることで、正しい論証のみを行うことができるようになるからである。そこで、任意の論証が入力として与えられたとき、「妥当」ないし「非妥当」というレッテルを出力として返すような機械を考え、これを「妥当性判定装置」と呼ぶことにし、妥当性判定装置が持ち得る性質のうち、次の三つに注目してみよう。

妥当性判定装置が性質（1）を持つとき、この装置は論理 L において「健全」と言われ、性質（2）を持つときは「狭い意味で完全」と言われる。性質（3）を持っているときの定まった名称はないが、ここでは「逆完全」と呼ぶことにする。また、性質（1）と（2）の両方を持つとき、妥当性判定装置は論理 L において「完全」と言われ、性質（1）、（2）、（3）を全部持つときは「決定可能」と言われる。
　健全性、弱い意味での完全性、逆完全性は単独ではあまり意味はない。どのような論証が入力されても即座に「非妥当」というレッテルを出力する妥当性判定装置は簡単に作ることができる。この装置は論理 L において妥当でない論証が入力されたときに「妥当」を出力することはない（なぜなら、常に「非妥当」を出力し、決して「妥当」を出力することはないから）。したがって、この装置はどの論理においても健全である。同じように、どのような論証の入力に対しても直ちに（ワンステップで）「妥当」を出力する装置も簡単に作れるが、この装置は任意の論理において弱い意味で完全である。逆完全も同様である。これに対して、完全な妥当性判定装置、および、決定可能な妥当性判定装置が存在するか否かはトリビアルな問題ではなく、おのおのの論理において探求されるべき問題である。論理 L において完全な妥当性判定装置が存在するときは、論理 L 自体も「完全」と呼ばれ、存在しないときは、論理 L は「不完全」と呼ばれる。同様に、論理 L において決定可能な妥当性判定装置が存在するときは、論理 L 自体も「決定可能」と呼ばれ、存在しないときは、論理 L は「決定不可能」と呼ばれる。
　完全性と決定可能性の関係について一つ注意しておくべきことがある。それは、妥当性判定装置が完全ならば、妥当な論証の入力に対して「妥当」を出力するのだから、非妥当な論証が入力されれば「非妥当」を出力するはずであり、結局、この装置は決定可能ではないか、という疑問に関してである。この疑問はもっともだが、間違いである。完全な妥当性判定装置は、妥当な論証が入力されれば、必ず有限回のステップの後に「妥当」を出力するが、非妥当な論証が与えられたとき、循環する手続きに入り込んでしまうなどの理由によって、いつまでたっても永遠に出力を出さないこともあるからである。永遠に出力を出さないことを見て取った後に「非妥当」を出力するようにすれば、完全な妥当性判定装置をもとにして決定可能な判定装置を作ることができるのではないかと思われるかもしれないが、これも不可能である。なぜなら、この妥当性判定装置は、永遠に出力を出さないことを見て取ったときには既に無限回のステップを経ているので、決定可能な判定装置が満たすべき「有限回のステップの後」という条件を満たしていないからである。完全だが決定可能でない妥当性判定装置が存在し、したがって、完全だが決定不可能な論理もあり得ることには注意しておきたい。^（1）
　論理 L が決定可能であれば、どんな論証が与えられても、ある与えられた既製の機械的な手続きにしたがって、有限回のステップの後に、それが妥当な論証の集合の要素になっているか、それとも非妥当な論証の集合の要素になっているのかを正しく決定することができる。これは論理のもっとも理想的なあり方である。
　次に、論理 L が完全だが決定不可能であるとすれば、任意の論証に関してそれが妥当であるか否かを機械的に決定することはできなくなるが、妥当な論証に関しては、それがどんな論証であっても、妥当であることを有限回のステップの後に正しく決定することができる。他方、非妥当な論証に関しては、それが非妥当であると決定するために機械的な妥当性判定装置に頼ることはできなくなる。どんな判定装置を使っても、「非妥当」という出力が出てこない非妥当な論証が存在するからである。そのため、非妥当であると正しく決定するためには、一般に、個々の論証に応じて各自が創意工夫をこらして考える必要がある。既製の機械的手続きに任せきることはできないのである。論理が持つこの性格は、論理を決まり切ったつまらないことと考える人にとっては、驚きであるかもしれない。
　最後に、論理 L が不完全であれば、論証の妥当性を説明するときにも機械的な妥当性判定装置に頼ることはできなくなる。どんな妥当性判定装置を作ったとしても、それが健全である限り、妥当な論証を入力しても「妥当」が出力されないような、そうした妥当な論証が存在するからである。したがって、不完全な論理では、一般に既製の機械的手続きに頼りきることはできないのであって、個々の論証に即して頭をつかい、論証が妥当であるか否かを決定しなければならない。6 節で明らかになるように、これが数学者の存在理由である。

5.　原子命題論理

　この節では、命題論理よりもさらに言語の意味の捉え方が粗い、非常に単純な論理を取り上げて、その完全性と決定可能性を証明する。この論理には一般的な名称がないので、仮に「原子命題論理」と呼ぶことにする。3 節で注意した命題論理と 1 階述語論理の包含関係と同様、原子命題論理で妥当とされる論証の集合は、命題論理で妥当とされる論証の集合の内に完全に含まれる。意味の捉え方は荒いが、この論理で妥当とされる論証はいかなる論理においても妥当であり、その意味でこの論理はきわめて基本的な論理なのである。
　原子命題論理は私たちの言語の意味を次のように捉える。

このように意味を捉えることによって原子命題論理で妥当な論証の集合が確定する。例えば、次の論証を考えてみよう。

前提「雪は白い」と「地球は丸い」がともに真ならば、結論「雪は白い」も必ず真になる。なぜなら、二値性より、雪は白く地球は丸いという世界の中では、「雪は白い」の真偽は変動しないからである。したがって、前提のすべてが真ならば結論も必ず真になるので、この論証は原子命題論理において妥当である。他方、次の論証を考えてみよう。

前提「雪は白い」と「地球は丸い」がともに真だが、結論「ソクラテスは人間である」が偽であるような世界は存在する。なぜなら、二値性と原子性によって、そうした世界が存在することは保証されているからである。したがって、前提のすべてが真で結論が偽になることが可能であるから、この論証は原子命題論理において非妥当である。
　では、個々の論証ではなく、論証一般の妥当性と非妥当性を私たちは機械的に決定できるのであろうか。答えはイエスである。そのことは、具体的な妥当性判定装置 J をつくり、原子命題論理におけるその健全性、弱い意味での完全性、逆完全性を証明することによって示される。
　任意の論証 A は次のような形をしている。

₁

₂

妥当性判定装置 J は、論証 A が入力されると、まず P₁ を取り上げて、それが C と同じ文であるか否かをチェックする。同じ文であれば「妥当」を出力して停止する。同じ文でなければ、次の P₂ に進み、それが C と同じかどうかをチェックする。同じなら「妥当」を出力し、同じでないなら P₃ に進み、同様の手続きを繰り返す。もしも P_n まで進み、これが C と同じ文でなければ、妥当性判定装置 J は「非妥当」を出力して停止する。
　妥当性判定装置 J の健全性は以下のように証明される。論証 A が入力されたときに妥当性判定装置 J は「妥当」を出力したとしよう。そうすると、妥当性判定装置 J の作り方から明らかなように、P₁, P₂, . . . , P_i, . . . , P_n のどれかが C と同じ文だったはずである。それを P_i としよう。すると、二値性より、P_i が真のときは C も真である。よって、P₁, P₂, . . . , P_i, . . . , P_n のすべてが真のときも C は真である。したがって、前提のすべてが真ならば結論も必ず真になるので、論証 A は原子命題論理において妥当である。以上より、妥当性判定装置 J は原子命題論理において健全である。
　妥当性判定装置 J の弱い意味での完全性は次のように証明される。上の論証 A を任意の妥当な論証とする。すると、P₁, P₂, . . . , P_i, . . . , P_n のすべてが真ならば C も真である。ところが、もし P₁, P₂, . . . , P_i, . . . , P_n のどれもが C と異なる文だとすれば、原子性より、P₁, P₂, . . . , P_i, . . . , P_n のすべてが真で C が偽であることが可能である。よって、P₁, P₂, . . . , P_i, . . . , P_n のどれかは C と同じ文でなければならない。C と同じ最初の文を P_i としよう。すると、論証 A が入力されると、妥当性判定装置 J は P_i まで進み、これをチェックし終えると「妥当」と出力する。これは、P₁ から始めて i 回のチェックの後で出力しているので、有限回のステップしか経ていない。以上より、妥当性判定装置 J は原子命題論理において弱い意味で完全である。
　妥当性判定装置 J の逆完全性の証明は以下の通り。上の論証 A を、こんどは任意の非妥当な論証とする。このとき、P₁, P₂, . . . , P_i, . . . , P_n のすべてが真だが C が偽になる場合が存在する。しかし、もし C が P₁, P₂, . . . , P_i, . . . , P_n のどれかと同じ文であるとすると、二値性より、P₁, P₂, . . . , P_i, . . . , P_n のすべてが真ならば C も真になってしまう。したがって、C は P₁, P₂, . . . , P_i, . . . , P_n のどれとも同じではない。すると、論証 A が入力されると、妥当性判定装置 J は P_n まで進み、これをチェックし終えると「非妥当」を出力する。それまでに実行したステップは有限回（n 回）である。以上より、妥当性判定装置 J は原子命題論理において逆完全である。
　妥当性判定装置 J は原子命題論理において健全で、弱い意味で完全であり、逆完全でもあるので、完全であり、しかも、決定可能である。よって、原子命題論理は完全であり、その上、決定可能である。

6.　原子命題論理を越えて

　原子命題論理は言語の意味をきわめて粗く捉えているので、そこで妥当とされる論証は非常に限られたものになってしまう。例えば、次の論証を考えてみよう。

原子命題論理の意味の捉え方によれば、この論証の前提が共に真で結論が偽であることは可能である（原子性により）。よって、この論証は原子命題論理においては非妥当である。しかし私たちの直観は、この論証は本来の論理において妥当であると告げている。そこで、言語の意味をもう少し細かく捉えて、妥当な論証の範囲を拡大する必要がある。この節では、その拡大の試みをいくつか概観しておく。
　原子命題論理より細かく意味を捉える最初の試みが命題論理である。命題論理の捉え方によると、私たちの言語は原子文と複合文の二種類からなる。そして、原子文に関しては、原子命題論理の考え方が正しいと認める。つまり、二値性と原子性が成立するのである。しかし、複合文に関しては事情が異なる。複合文とは、いくつかの原子文が「ない」、「かつ」、「または」、「ならば」などの結合子によって結びつけられたものであり、その真偽は原子文の真偽と結合子の意味に依存して定まる（つまり、複合文では原子性が成り立たない）。その結果、常に真（あるいは偽）になる文も存在する（つまり、複合文では二値性の一部が成り立たない）。命題論理はこの結合子の意味を具体的に捉える。例えば、「かつ」の意味は「『P』と『Q』が共に真のとき、かつ、そのときに限り、『P かつ Q』は真である」というように捉えられる。このような仕方で言語の意味が捉えられることによって、命題論理で妥当な論証の集合が確定する。例えば、先に見た原子命題論理で非妥当な論証は、命題論理では妥当になる。命題論理は、原子命題論理と同様、完全であり決定可能であることが判明している。
　意味を細かく捉える次の試みが 1 階述語論理である。1 階述語論理は原子文と複合文の区別を受け継ぐが、原子文の内部構造にまで踏み込み、その構成部分の意味から捉えようとする。すなわち、原子文は述語と項からなるとされ、項はどんな個物をも指示することができ、述語は個物の集合や個物のペアの集合などを任意に指示することができる、というように項と述語の意味は捉えられる。原子文の真偽は項の指示する個物（ないし項のペアが指示する個物のペアなど）が述語の指示する集合の要素になっているか否かによって決定される。例えば、文「地球は丸い」は、項「地球」と述語「丸い」からできている。項「地球」が太郎を指示し、述語「丸い」が男性の集合を指示しているなら、文「地球は丸い」は真である。他方、項「地球」が数 2 を指示し、述語「丸い」が奇数の集合を指示しているなら、文「地球は丸い」は偽である。複合文の真偽は原子文、結合子、および、新しく着目される量化子（「すべて」と「ある」）の意味によって決定される。結合子の意味は命題論理のときと同じである。量化子の意味も、その語に対する私たちの直観的な理解にしたがって具体的に捉えられる。詳細は省略するが、このような仕方で意味を捉えることによって、1 階述語論理で妥当な論証の集合が確定する。例えば、2 節の最初に見た論証は、原子命題論理においても命題論理においても非妥当だが、直観的には妥当であり、実際、1 階述語論理では妥当である。1 階述語論理は完全であることが判明しているが、決定不可能であることも分かっている。つまり、1 階述語論理で非妥当な任意の論証を決められた機械的な手続きで非妥当であると決定することは一般にできないのである。
　さらに意味を細かく捉えると、「同一性と関数をもった 1 階述語論理」と呼ばれるものが得られる。この論理は、まず、同一性述語（「x=y」や「x は y と同じである」など）の意味を具体的に特定する。つまり、単なる 1 階述語論理では、同一性述語は個物のペアの集合を任意に指示できると考えられており、他の述語と全く同じように扱われていたが、この論理では同一性述語の指示対象は同一の個物のペアの集合であると特定されることになる。次に、項が単項と複合項に区分される。例えば、以前は「太郎の母」は「太郎」と区別されなかったが、ここでは前者は関数表現「の母」と単項「太郎」からなる複合項であるとされる。複合項の指示対象は単項の指示対象と関数表現の意味によって決定される。ただし、関数表現は任意の関数を意味するとされ、具体的にどの関数を意味するのかは特定されない。こうしてできあがる論理も決定不可能だが完全であることが証明されている。
　最後に見ておきたい論理が一階述語論理に付け加えられた形での自然数論である。これは今まで特定されていなかった関数表現「＋」、「×」の意味である関数を、それぞれ和と積であると特定する。また、同じく不特定であった項「0」、「1」、「2」、・・・の意味である指示対象を、それぞれ数 0、数 1、数 2、・・・であると特定する。このように算術に関わる表現の意味を特定して捉えることによって、自然数論という論理で妥当な論証が確定する。例えば、次の論証を考えてみよう。

これは直観的に言って妥当な論証である。前提が真ならば、そこに含まれる表現の意味のみによって、世界の偶然的な在り方とは関係なく、結論も真になると考えられるからである。そして実際、この論証は自然数論では妥当とされる。自然数論は決定可能でないどころか、完全でさえないことが証明されている。自然数論における論証の妥当性を示すことは、一般に機械的な手続きによっては不可能であり、数学者の才能と努力にゆだねられているのである。

7.　おわりに

　最後に本論文の副題の意味を説明しておかなければならないだろう。ここで主題的に取り上げた論理には「原子命題論理」という名称を与えたが、それは命題論理とのつながりを意識したからである。しかしこの論理は伝統的には「女の理由」と呼ばれているものを一般化したものである。

そう思うからそう思う

^（2）

シェイクスピアが正しく見抜いたように、女の理由は私たちの思考を支配しているきわめて基本的な論理であり、しかもそれは完全な論理であり、かつ、決定可能な論理である。

註

（1）論理学の教科書の多くでは、公理系を使って論理の完全性が説明されており、それと本論文における完全性の説明はどういう関係にあるのか疑問に思われるかもしれない。この註では、両者の関係を明らかにし、同時に、完全だが決定不可能な妥当性判定装置の例を多少具体的に記述しておきたい。
　公理系は、「公理」と呼ばれる有限個の文と、有限個の「推論規則」と呼ばれるものからなる。推論規則は、例えば「ある文からその二重否定文を導くことができる」のように、あるタイプの文から導いてもよい文のタイプを定めた規則である。公理や推論規則が異なれば、異なる公理系が得られる。
　さて、論証 A が次のような形をしているとする。

₁

₂

また、有限個の文の列Γが次のような形をしているとする。

₁

₂

このとき、文の列Γが以下の条件を満たすならば、文の列Γは論証 A の公理系 AS における「証明」であると言われる。

　公理系 AS は論理 L において次のような性質も持つかもしれない（星印は本文の用語と一応区別するためであって、実際には付かない）。

論理 L において健全*で、かつ、弱い意味で完全*でもある公理系 AS は「完全*」と呼ばれる。完全*な公理系が存在するような論理も「完全*」と呼ばれる。
　さて、論理 L は完全*であることが示されたとしよう（つまり、論理 L には完全*な公理系 AS が存在することが示されたとしよう）。このとき、次のような仕方で妥当性判定装置 JA を作ることができる。まず、有限個の文の列（つまり、文を有限個並べることによって得られる列）は無限個存在するが、その全部を次のように自然数に対応させて一列に並べる（これが可能であることの説明は省略する）。

₀

₁

₂

論証 A が入力として与えられたら、妥当性判定装置 JA は、まず、文の列Γ₀ を取り上げ、それが論証 A の公理系 AS における証明になっているか否かをチェックする。Γ₀ に含まれる文の個数、論証 A の前提の個数、公理系 AS の公理の個数と推論規則の個数は、すべて有限個であるから、このチェックは有限回のステップで完了する。チェックの結果、証明になっていることが判明すれば、妥当性判定装置 JA は「妥当」を出力して停止する。証明になっていないことが判明すれば、Γ₁ を取り上げ、同様のチェックを行い、それが証明になっていれば「妥当」を出力し、そうでなければΓ₂ に進む。以下同様である。文の列をすべてチェックして、そのどれもが論証 A の証明になっていないことが判明すれば、妥当性判定装置 JA は「非妥当」を出力して停止する。
　この妥当性判定装置 JA が論理 L において本文で述べた意味で「健全」であることは明らかである。論証 A の入力に対して「妥当」が出力されたとき、ある文の列Γ_n が論証 A の公理系 AS における証明になっているが、公理系 AS は健全*であると仮定されているので、論証 A は論理 L において妥当となっているからである。妥当性判定装置 JA が論理 L において本文の意味で「弱い意味で完全」であることも明らかである。論証 A を論理 L において妥当な任意の論証とする。公理系 AS の弱い意味での完全性*の仮定より、論証 A の証明となっている有限個の文の列Γが存在するが、これは有限個の文の列である以上、それをすべて列挙した Γ₀, Γ₁, Γ₂, . . . , Γ_n, . . . のどこかに位置しているはずである。それをΓ_n としよう。すると妥当性判定装置 JA はΓ_n のチェックを終了した段階で「妥当」を出力する。おのおのの列のチェックは有限回のステップで完了し、それを n+1 回繰り返すだけであるから、全体でも有限回のステップの後に「妥当」が出力される。よって、これは「弱い意味で完全」である。それゆえ、妥当性判定装置 JA は論理 L において本文で述べた意味で「完全」である。したがって、論理 L は本文の意味で「完全」である。以上より、論理 L の完全性*を示すことは、本文の意味での「完全性」を示すことに他ならないことが分かった。
　では、妥当性判定装置 JA は逆完全であろうか。これが「非妥当」を出力するのは、入力がどんな非妥当な論証であるかに関係なく、有限個の文の列をすべてチェックし終わった後である。ところが、有限個の文の列は無限個存在するので、「非妥当」を出力するのは無限回のステップを実行した後である。よって、逆完全ではない。したがって、妥当性判定装置 JA は完全だが決定不可能な妥当性判定装置なのである。

（2）山下正男、『論理的に考えること』、岩波書店、1985年、22-3頁。

（はしもと・こうじ　筑波大学哲学・思想学系助教授）