科目名:現代論理学
担当教員:橋本康二
単位数:2 標準履修年次:2〜4 実施学期:1 曜時限:月6・木6
I. 主旨
現代思想や科学哲学などを学んでいく上で必要になる論理的推論能力を鍛える。健全性、無矛盾性、完全性などのメタ論理的帰結はあつかわない。あくまで論理的に正しく推論する実際の力を身につけることが、この授業の目標である。
II. 内容
以下の本を教科書として使用する。
ジョン・バーワイズ、ジョン・エチメンディ、『論理学の基礎と演習』、大沢秀介・白旗優・中川大・中戸川孝治・橋本康二訳、慶應義塾大学出版会、2006年
この本ではきわめて初等的な論理から始まって、命題論理、一階の述語論理、集合論の基礎と数学的帰納法へと論理が展開されていて、基本的な論理はすべてカバーされている。また、メタ論理の話題として、一階の述語論理の健全性と完全性の厳密な証明も与えられている。しかし本授業では、時間の制約があるので、一階の述語論理の基礎的な部分(限量子の基本的な使い方)までをマスターすることを目標にする(最低でも命題論理の範囲は全部マスターしてもらう)。その部分の教科書の目次は以下の通りである。
第 I 部 命題論理
第 1 章 原子文
1.1 個体定項
1.2 述語記号
1.3 原子文
1.4 一般的な一階言語
1.5 関数記号(オプション)
1.6 集合論の一階言語(オプション)
1.7 算術の一階言語(オプション)
1.8 別の表記法(オプション)
第 2 章 原子文の論理
2.1 妥当で健全な論証
2.2 証明の方法
2.3 形式的証明
2.4 Fitchで証明を構成する
2.5 非帰結を立証する
2.6 別の表記法(オプション)
第 3 章 ブール結合子
3.1 否定記号: ¬
3.2 連言記号: ∧
3.3 選言記号: ∨
3.4 ゲームについての注意
3.5 多義性とカッコ
3.6 同値な語り方
3.7 翻訳
3.8 別の表記法(オプション)
第 4 章 ブール結合子の論理
4.1 トートロジーと論理的真理
4.2 論理的同値性とトートロジー的同値性
4.3 論理的帰結とトートロジー的帰結
4.4 Fitch におけるトートロジー的帰結
4.5 否定を動かす(オプション)
4.6 連言標準形と選言標準形(オプション)
第 5 章 ブール論理の証明方法
5.1 妥当な推論ステップ
5.2 場合分けによる証明
5.3 間接証明:矛盾による証明
5.4 矛盾した前提をもつ論証(オプション)
第 6 章 形式的証明とブール論理
6.1 連言の規則
6.2 選言の規則
6.3 否定の規則
6.4 部分証明の正しい使い方
6.5 戦略と戦術
6.6 前提のない証明(オプション)
第 7 章 条件文
7.1 実質的条件記号: →
7.2 双条件記号: ⇔
7.3 会話の含み
7.4 真理関数的完全性(オプション)
7.5 別の表記法(オプション)
第 8 章 条件文の論理
8.1 非形式的な証明の方法
8.2 → と ⇔ に関する証明の形式的規則
8.3 健全性と完全性(オプション)
8.4 妥当な論証: いくつかの復習問題
第 II 部 限量子
第 9 章 限量入門
9.1 変項と原子論理式
9.2 限量子記号: ∀ と ∃
9.3 論理式と文
9.4 限量子の意味論
9.5 4 つのアリストテレス文型
9.6 複合名詞句の翻訳
9.7 限量子と関数記号(オプション)
9.8 別の表記法(オプション)
論理をマスターするとは、様々な論理的概念や定義を理解し暗記するということを意味するのではなく、実際に論理にしたがって正しく推論できるようになることを意味している。最低でも命題論理の範囲までをその意味でマスターしてもらいたい(つまり命題論理にしたがって正しく推論できるようになってもらいたい)。なお、以下のサイトに教科書の一部(全体の目次と第1章と第2章の本文)の PDF ファイルを置いておくので、授業内容の参考にしてもらいたい。(このサイトは学外からはアクセスできない。また、ダウンロードしたファイルを他人に配布しないこと。)
http://www.sakura.cc.tsukuba.ac.jp/~khashimo/campus/LPLbook_to_2.pdf
[授業の進め方]
教科書には、意味論を理解するための Tarski's World、形式的証明を構成するための Fitch、真理表を作成するための Boole、練習問題の解答を提出するための Submit という4つのコンピューター・ソフトウェアを収めた CD-ROM が付属していて、読者は適宜これらのソフトウェアを用いながらテキストを読み進めて論理学を学んでいくことになる。最もよく使われるのは Tarski's World であり、下の画像はその画面の一つである。
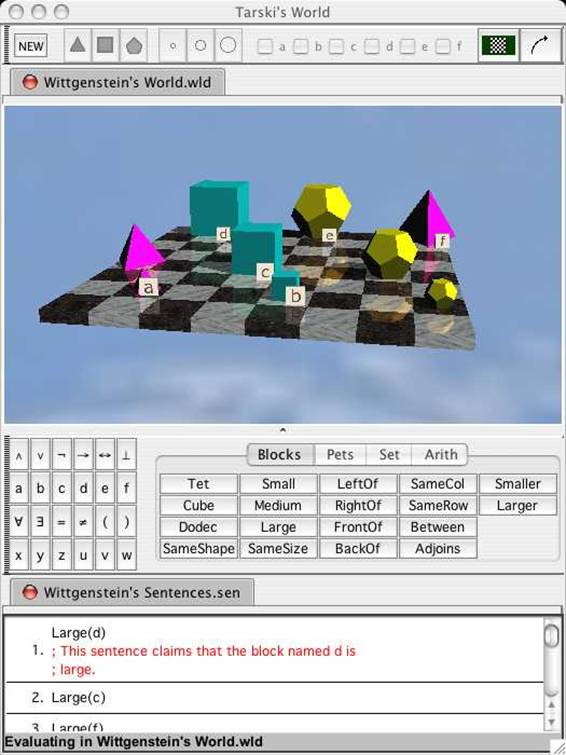
ここでは盤上に配置された立体図形の形や大きさや相互の位置関係などを論理的に表現する訓練が行われる。次によく使われるのが Fitch である。
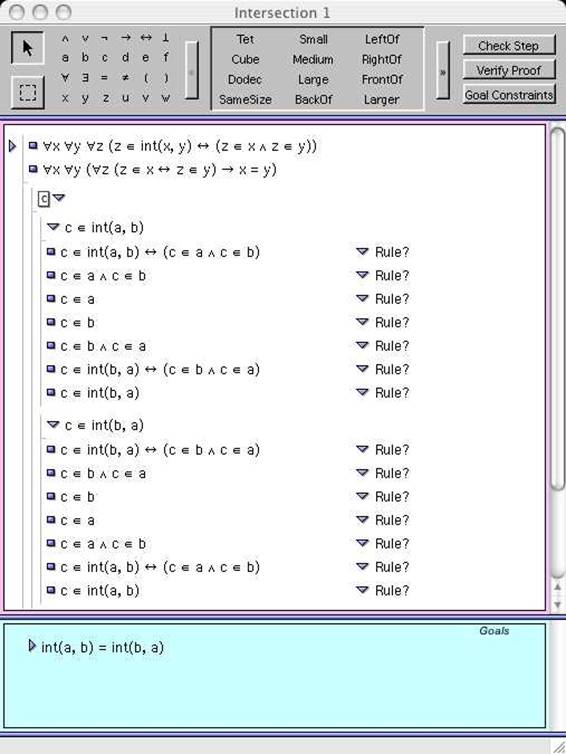
ここでは与えられた命題の証明をコンピュータとの対話形式で一歩一歩構成することが行われる。Boole は以下のような真理表の作成に使われる。
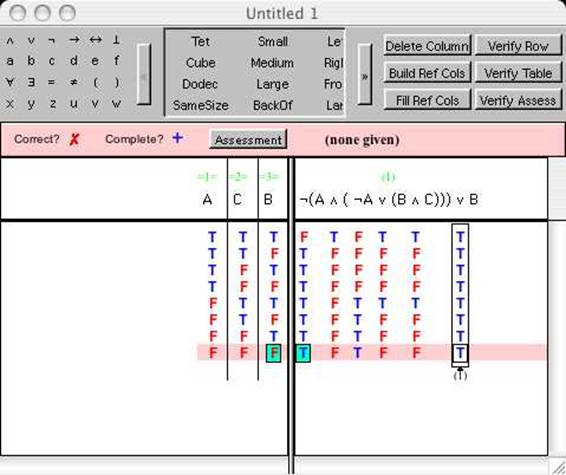
この真理表を使って、命題の持つ論理的性質をチェックすることができる。
授業は比較文化学類コンピュータ室で行われ、受講生はコンピュータにインストールされたソフトウェアを用いながら各自で教科書を読み、論理学の学習を進めていく。担当教員は受講生の作業に助言を与え、また受講生からの質問に対して答える。したがって、講義は行われない。教科書にはセクションごとに多数の練習問題が与えられていて、これを解くことが学習作業の中心を占めることになる。練習問題には二種類ある。一つはオーソドックスなタイプの練習問題で、この場合、受講生は紙に解答を書いて担当教員に提出し、担当教員はこれを添削して受講生に返却することになる。もう一つのタイプの練習問題では、受講生は上記のソフトウェアを使ってファイルを作成し、それを Submit ソフトウェアを使ってインターネット経由で採点サーバーに提出することになる(下図参照)。
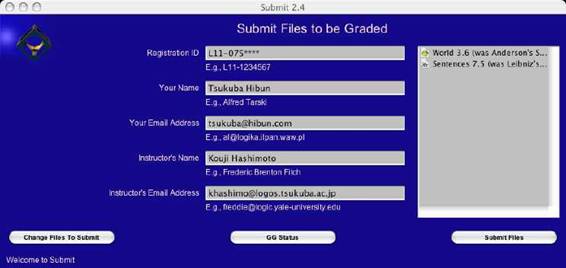
提出されたファイルは採点サーバー(Grade Grinder)によって採点され、結果は電子メールで受講生に通知される(下図参照)。
受講生は各自のペースで学習を進めてかまわない。練習問題も適宜取捨選択してよい。ただし、理解が不十分だと感じたセクションの練習問題は必ず解いてもらいたい。
III. 評価方法・基準
授業期間中に多数の練習問題の解答を提出してもらい、試験期間中には個別に口頭試験を行う。その結果を見て、命題論理を用いた推論を適切に行えるようになったと判断された受講生に対しては A を与える。なお、命題論理の範囲(上の目次の8.4まで、ただしオプションは除く)の学習が完了しなかった場合は評価の対象外になるので注意すること。
IV. 参考文献
教科書以外は特に読む必要はない。
V. その他
(1)授業に来ていきなり練習問題を解くことは不可能なので、授業の前に2時間ほどかけて教科書の本文を予習しておく必要がある。練習問題を解く作業は授業時間中に行えばよいが、それ以外の時間にも可能な限り自主的に練習問題に取り組むことが強く望まれる。(ソフトウェアは各自のパーソナル・コンピュータにインストールして使用することもできる。また、CD-ROM からも起動できるので、比較文化学類コンピュータ室以外の他の共用コンピュータでもソフトウェアを使用することは可能である。)
(2)ソフトウェアで提出された練習問題の解答はスタンフォード大学とシカゴ大学に設置されたサーバーで採点される。教科書を購入することによってインターネット経由でこのサーバーにアクセスする権利が与えられるので、受講生は必ず教科書を購入すること。
(3)初回の授業には必ず出席すること。出席しなかった場合、受講は認められない。コンピュータの台数には限りがあり、受講希望者が多い場合は人数制限を行うこともあるので、必ず出席してもらいたい。
(4)コンピュータの使用方法についての最低限の知識を持っていることが前提される。少なくとも電子メールのアカウントを持っていて(携帯メールは不可)、それを自由に使うことができなければならない。また、ソフトウェアは上の画像で明らかなように日本語化されておらず、採点結果を伝える電子メールも英語で書かれているので、ある程度の英語の読解力も必要である。
(5)1学期のオフィスアワーは水4と木5。研究室は人社棟 A819。